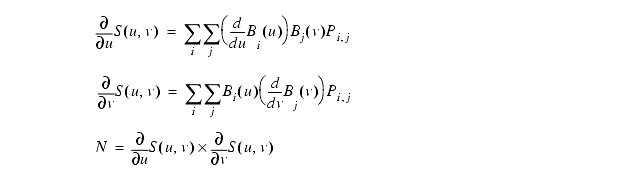6.3 SURFACE PATCHES

---

Surfaces are typically defined with a variety of techniques. These include,

- fixed primitives

- swept surfaces

- rotated surfaces

- splines/free form

6.3.1 Fixed Primitives

These are basic geometric shapes defined either explicitly, or parametrically. These often include,

- spheres

- cylinders

- cones/conics

- saddles

- ellipsoids

- toroids

- squares/rectangles

- wedges

- planes

Normal analytical geometry is used for these shapes.

6.3.2 Swept Surfaces

Basically we start with a line in space, and sweep it through space to define a surface.

A swept surface is normally represented parametrically,

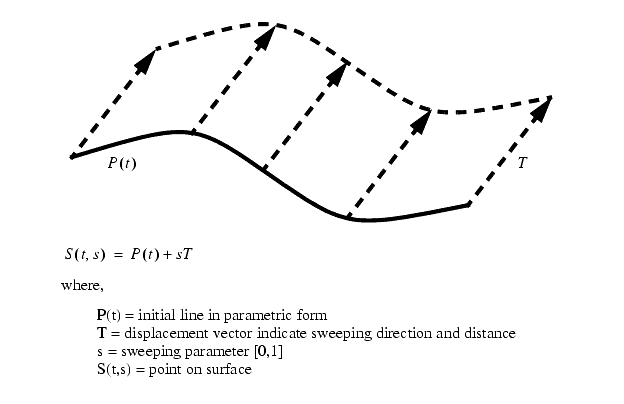
The displacement vector T could also be a curved line. When the line is straight we often call the surface extruded.

6.3.3 Rotated Surfaces

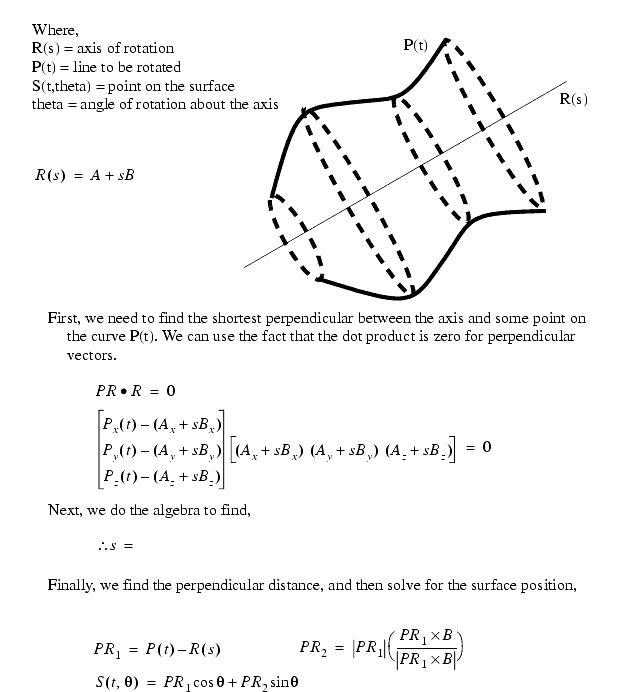
This approach is much like the swept, except there is a central axis that we rotate about.

Basically to rotate a section we define an axis of rotation, and rotate the line profile.

6.3.4 Free Form Splined Surfaces

Basically, we can look at a splined surface as composed of normal spline curves.

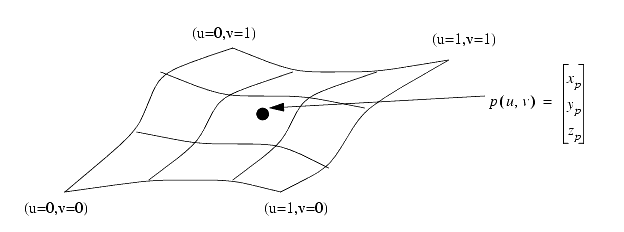
Procedure for using splines in 3D,

1. Take a surface divided over an area, and break it into regions.

2. For each region find points needed for the spline. Here there are 16 shown in a 4 by 4 grid.

3. Use the measured x,y,z-points to calculate spline parameters in the u direction for each line of points, and then in the v direction.

4. To find new z-points use (x, y) to find the appropriate patch. Convert (x, y) to (u, v). Substitute (u, v) into splines to find estimated z-value. The calculation shown below uses the blending functions.

Surface normals can be calculated using partial derivatives. (Note: these are very important for many functions, such as rendering)