1.6.1 Data Structures for Boolean Equation Storage

As shown before, each term is represented in a LISP like fashion with an operator being first in the list, followed by a list of operands. An example of this equation form is shown in Figure 1.2 Nested Boolean Algebra Data Structure, along with a data structure diagram that is used to store the equation (only part of the equation is shown for the purpose of clarity). The Operation List may be thought of as storing the start of each nested term, it coincides with the open bracket ‘(‘ and the operator. Therefore, each operator is assigned a row. The row points to a list of terms. The other field in the row is for a symbol pointer. The Symbol Pointer allows a text string (and other symbol information) to be associated with each operation. The append list field allows lists of appended properties, such as ‘test’, to be appended to symbols and terms.

The Term Lists array is simply for storing lists of arguments for the operations. The reader will note that the pointer refers to both the Operation List, and the Symbol List. This allows both sets, like ‘A’ and sub-terms ‘(+ D G)’ to exist in common. The ‘type’ field specifies which type of pointer is in the ‘pointer’ field. The ‘point to next’ field provides a linked list of the arguments, and terminates with a ‘last’ marker.

Finally, the Symbol list is used to store textual information for recall by the user. These also contain two fields for use by the calling routines. A ‘pointer’ field is provided so that the user may store a reference to an outside object (like a geometric primitive), whereas a ‘type’ field provides information about the pointer type. There are additional types of data associated with each list for the purposes of maintenance, as is described on the next paragraph.

 

Figure 1.2 Nested Boolean Algebra Data Structure

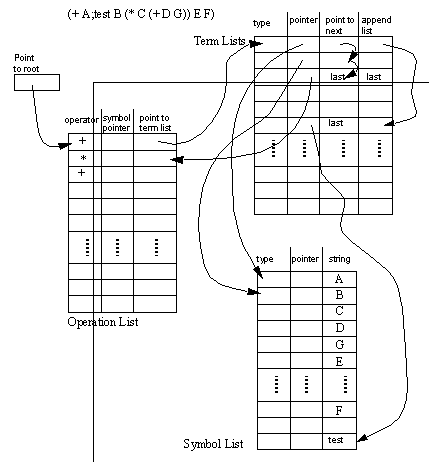
(Only a partial example is given for clarity)

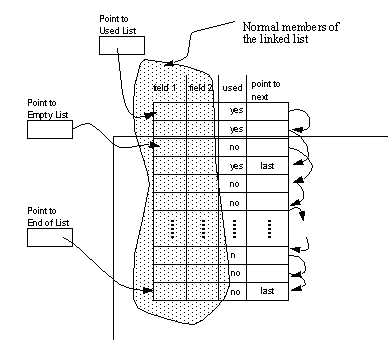
The reader should note that the data structures in Figure 1.2 Nested Boolean Algebra Data Structure do not show the method for dynamic memory allocation. The lists shown in the data structure have many rows which will be added and deleted in a semi-random fashion. As a result, a reuse mechanism structure has developed for each of the lists. One example of this structure is shown in Figure 1.3 Dynamic Memory Structures Added to Lists, and may be viewed as a generic approach for all of the lists above. In Figure 1.2 Nested Boolean Algebra Data Structure both ‘used’ and ‘point to next’ are added data fields. This structure makes allocation of a new row, simply a matter of deleting from the head of empty linked list, and pushing onto the head of the used list. Deletion of an existing term is a case of modifying next pointers to point over the defunct term, then pushing the now empty term onto the empty list. The used and unused flags are updated to make validity checking easier, without having to retrace lists. The end of list pointer makes range checking easy, when the array has been dynamically allocated (as was done using C++).

 

Figure 1.3 Dynamic Memory Structures Added to Lists

Public functions have been created to manipulate each object. These are structured so that the functionalities are nested. Some of the functions are listed below.

Symbol List:

• Initialize a new symbol.

• Find a defined symbol by name.

• Set/Get a pointer value for the symbol.

• Set/Get a pointer type for the symbol.

• Set/Get a pointer name for the symbol.

• Remove an unused symbol.

 

Terms Lists:

• Create a new term list.

• Append/Insert a term to a list.

• Remove a term from a list.

• Remove a term list.

• Copy a term list.

• Get an individual term reference from a list (e.g. 3rd term in a list).

• Get/Set a term type (symbol, or operation).

• Get/Set a term pointer (e.g. pointer to symbol list).

• List/Count all terms in a list.

 

Operation List:

• Create a new operation.

• Remove an unused operation.

• Find a term/symbol in the equation.

• Address term list operations with respect to equation.

• Copy a branch in the equation.

• Dump/Import a string which represents the equation.

• List/Count terms/symbols in an equation.

This list has many functions, but as a group they enable storage, and manipulation of boolean expressions. When referring to individual terms/symbols in the expression their location may be addressed by a simple scheme. For example, the address ‘:2:2:2’ in the equation ‘(+ A B ( * C D (+ E F G H)’ would refer to the symbol ‘G’. For the same equation, address ‘:2’ (or ‘:2:’) would refer to the term ‘( * C D (+ E F G H ) )’, and address ‘:’ refers to the entire equation. This lays the ground work for a systematic addressing of the equation for boolean algebra.