1.6 Case Study

---

A typical vibration control system design is described in Figure 1.44.

Figure 1.44 A vibration control system

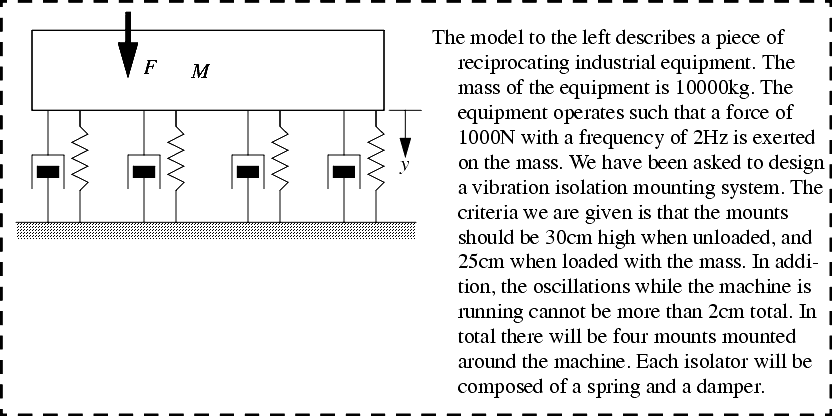
There are a number of elements to the design and analysis of this system, but as usual the best place to begin is by developing a free body diagram, and a differential equation. This is done in Figure 1.45.

Figure 1.45 FBD and derivation of equation

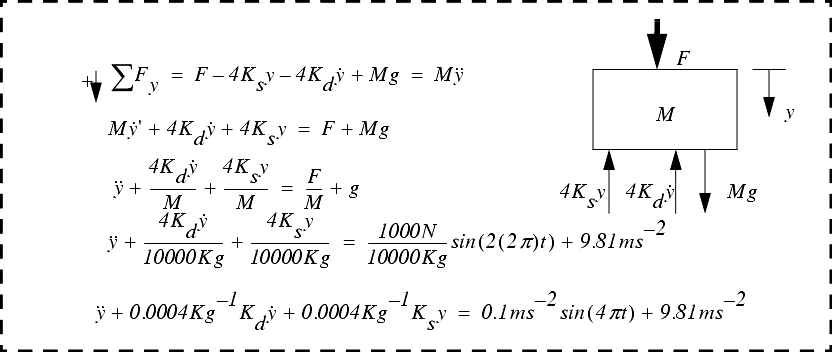
Using the differential equation, the spring values can be found by assuming the machine is at rest. This is done in Figure 1.46.

Figure 1.46 Calculation of the spring coefficient

The remaining unknown is the damping coefficient. At this point we have determined the range of motion of the mass. This can be done by developing the particular solution of the differential equation, as it will contain the steady-state oscillations caused by the forces as shown in Figure 1.47.

Figure 1.47 Particular solution of the differential equation

The particular solution can be used to find a damping coefficient that will give an overall oscillation of 0.02m, as shown in Figure 1.48. In this case Mathcad was used to find the solution, although it could have also been found by factoring out the algebra, and finding the roots of the resulting polynomial.

Figure 1.48 Determining the damping coefficient

The values of the spring and damping coefficients can be used to select actual components. Some companies will design and build their own components. Components can also be acquired by searching catalogs, or requesting custom designs from other companies.