1.3.1 Equation Templates

There is a structural relationship between the 8 process groups, and the Boolean form of equations. The list below shows some examples of the Boolean equation templates, and the processes they are associated with (templates are covered in more detail later).

1) ... ( ~ ( ~ A ) ) ... Molding shape A (molding)

2) ... ( & ... ( ~ ... A ... ) ... ) ... Cutting off shape A (milling)

3) ... ( & ... ( ~ ... A ... ) ... ) ... Machining out cavity of shape A (drilling)

4) ... ( & A B ... ) ... From shape A cut off shape B (sawing)

5) ... ( + A B C ) ... Join shapes B and C to A (welding)

6) ... ( : A B C ... ) ... Assemble parts B, C, ... to base part A (robot)

7) ... A ... Finish part A (part A has color=red, so paint)

8) ... A ... Part A has a feature that calls for forming

9) ... A;move ... Move part A (robot)

The form used in this list indicates where other arguments may exist by using ‘...’. Also note that the interpretation is sensitive to the content of the sets. For example, if 2) and 3) are compared, if ‘A’ is a cylinder then 3) would be the obvious choice. If ‘A’ is a box, or a half-space, then 2) would be the logical choice. Using these cases a set of manufacturing rules may be developed. These rules will use the form of the equation, and the (somewhat arbitrary) set properties to select a manufacturing process. As can be seen this list is limited, but still suggests how the templates can be matched up to various manufacturing processes. The reader is also directed to 7) and 8) above. Both of these are identical, and are only differentiated by the properties in the sets.

1.3.2 Data Structures for Rule Storage

The rules are stored in a hierarchical manner. The list contains,

1. a group of equation templates, where each refers to rules they may fire,

2. conditions (to be used by rules),

3. rules, including conditions to be satisfied, and results,

4. results to be performed when a rule is satisfied.

This approach requires a large degree of refinement in the future, but for now it is sufficient to provide the rule matching information. The rule structure has been chosen to be intentionally segmented, so that results, conditions, and rules may be reused when possible, therefore reducing the number of comparisons. The structure can be logically discussed within the context of the example in Figure 1.1 Part of a Rule File below (keep in mind that this example is in no way complete).

 

equation_form EQN_1 {

EQUATION: ( & ...( ~ VAR:V:0 ):LABEL:REF

RULE: drill_hole

RULE: chamfer_drill

}

equation_form EQN_9 {

EQUATION: (> : VAR:V:0 VAR:V:1 ...)

RULE: assemble_parts

}

rule assemble_parts {

EQUATION: ( & PART_0_EXISTS PART_1_EXISTS )

RESULT: ASSEMBLE_PARTS

}

rule drill_hole {

EQUATION: ( & CYLINDER_SHAPE DRILL_SIZE )

RESULT: DRILL_HOLE

}

rule chamfer_drill {

EQUATION: ( & CONE_SHAPE DRILL_SIZE )

RESULT: DRILL_CHAMFER

}

condition PART_0_EXISTS {

COMPARE ( V0.form $ )

}

condition PART_1_EXISTS {

COMPARE ( V1.form $ )

}

condition CYLINDER_SHAPE {

COMPARE ( V0.form == CYLINDER )

}

condition CONE_SHAPE {

COMPARE ( V0.form == CONE )

}

condition DRILL_SIZE {

MATH ( V0.ratio = V0.height / V0.radius )

ASSIGN ( V0.minimum = 0.5 )

COMPARE ( V0.ratio > V0.minimum )

COMPARE ( V0.ratio < 20 )

COMPARE ( V0.radius > 0.05 )

COMPARE ( V0.radius < 2.5 )

COMPARE ( V0.height > 0.1 )

COMPARE ( V0.height < 15.0 )

}

 

Figure 1.1 Part of a Rule File

 

 

 

 

 

 

 

 

result DRILL_HOLE {

EQUATION_DELETE_VARIABLE_TERM ( REF )

ADD_SET ( DRILL_HOLE )

ADD_PROPERTY ( DRILL_HOLE a1 = 0.5 )

ADD_PROPERTY ( DRILL_HOLE a2 = 1.0 )

ADD_PROPERTY ( DRILL_HOLE height = 0.0 )

PROPERTY_FUNCTION_VARIABLE ( DRILL_HOLE height + V0 height )

PROPERTY_FUNCTION_NUMBER ( DRILL_HOLE height / 20.0 )

PLAN_PUSH_TEXT ( ‘ DESCRIPTION ( drill hole ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( FEATURE single diameter hole ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( MACHINE qa1000 ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( MATERIAL t-7075 ) ‘ )

PLAN_PUSH_FORMAT ( ‘ CUTTING ( PARAMETERS ‘ DRILL_HOLE.height

DRILL_HOLE.a1 DRILL_HOLE.a2 ‘ ) ‘ )

// A costing section is added here for a trial run

ADD_PROPERTY ( DRILL_HOLE cost = 0.0 )

PROPERTY_FUNCTION_VARIABLE ( DRILL_HOLE cost + V0 height )

PROPERTY_FUNCTION_VARIABLE ( DRILL_HOLE cost * V0 radius )

PROPERTY_FUNCTION_NUMBER ( DRILL_HOLE cost * 1250.25 )

PROPERTY_FUNCTION_NUMBER ( DRILL_HOLE cost + 0.25 )

DECLARE_COST ( DRILL_HOLE cost )

}

result DRILL_CHAMFER {

EQUATION_DELETE_VARIABLE_TERM ( REF )

ADD_SET ( CHAMFER_HOLE )

ADD_PROPERTY ( CHAMFER_HOLE a1 = 0.5 )

ADD_PROPERTY ( CHAMFER_HOLE a2 = 1.0 )

ADD_PROPERTY ( CHAMFER_HOLE height = 0.0 )

PROPERTY_FUNCTION_VARIABLE ( CHAMFER_HOLE height + V0 height )

PROPERTY_FUNCTION_NUMBER ( CHAMFER_HOLE height / 20.0 )

PLAN_PUSH_TEXT ( ‘ DESCRIPTION ( drill chamfer ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( FEATURE Front Countersunk Hole ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( MACHINE qa1000 ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( MATERIAL t-7075 ) ‘ )

PLAN_PUSH_FORMAT ( ‘ CUTTING ( PARAMETERS ‘ CHAMFER_HOLE.height

CHAMFER_HOLE.a1 CHAMFER_HOLE.a2 ‘ ) ‘ )

}

result ASSEMBLE_PARTS {

EQUATION_DELETE_TERM ( :1 )

PLAN_PUSH_TEXT ( ‘ DESCRIPTION ( add part to fixtured part ) ‘ )

}

 

Part of a Rule File (cont’d)

The ‘equation_form’ sets identify possible templates that the equation may be matched to. This is obviously to drive a pattern matching system that identifies possible candidates from each expression. This pattern matching is likely to turn up a good number of candidates from each Boolean expression. After these candidates have been matched, all ‘RULE:’s identified in each matching ‘equation_form’ are checked. The conditions of the ‘rules’ are determined by the ‘EQUATION:’ field. The equation is interpreted for Boolean truth using the conditions as the logical statements. If the equation yields a Boolean truth, then all of the ‘RESULTS:’ are performed. The conditions are simple, they allow some simple calculations using ‘MATH’ and ‘ASSIGN’, and comparisons using the ‘COMPARE’ statements. If any of these items fail, then the condition fails.

The most structured part of the rules are the results. The various operations here will be described in detail later, but for now it is useful to point out that the results section can create new sets, alter their properties, alter the equation structure, and report on costs of the results. The rules sections also add steps to the process plan. The system internally keeps the effects of rules isolated so that the effects of a rule firing will only affect rules performing subsequent operations. This allows the process planning options to be done in a tree structure. If we wish to return to a previous state, then the complete state information is stored and no backwards reconstruction is required.

1.3.3 Equation Templates

If patterns are to be found within the equation structure, then we must have a method for describing these patterns. A method was developed for describing these patterns. There are two requirements of templates for doing this matching. First the templates should be able to represent any number of fixed and variable forms that the equation could match. Secondly, if variable equation forms are to be used, then variables must be available, so that the rules may refer to equation members through abstractions. The template form has a number of basic elements,

 

( X Start of a term, where ‘X’ is ‘?’ for any operator, or ‘+, &, :, ~’

for a specific operator.

) End of a term.

VAR:name:i

Refers to a variable list of all sets within a term (not including sets).

VAR:name:x

As above, but where the variable is ‘x’ position from the start.

(> This refers to the start of the expression only.

...( Allows a list of variables to be ignored before the start of a term.

...) Allows a list of variables to be ignored before the end of the term.

):LABEL:X

Allow a variable ‘X’ name to be bound to a term.

):VAR:X Assigns all of the properties of a term to be given a variable name.

VAR:name:i:prop

Same as above, but now it must have properties.

This list of elements can then be strung together to set up a template for matching. The author has written a simple algorithm for matching these templates to given equation segments, using a piecewise comparison. An example of this is given below.

EQUATION: ( & ( ~ B ) ( ~ C ) ( & A E ) ( ~ D ) ) (5.1)

TEMPLATE: ( & ...( ~ VAR:V:0 ):LABEL:REF (5.2)

The template given could be for a hole drilling operation. To begin, the algorithm examines the equation, and template one token at a time from left to right. In this example, both the template, and equation begin with a ‘(‘, and so the comparison continues. Next, the ‘&’ operation matches for both, and the comparison continues. The template string then has a ‘...(‘ condition that is fulfilled because the equation has a ‘(‘, but if there were variables before it, they would have been skipped. Next, the ‘~’ operator is matched. Next, the ‘VAR:V:0’ operator is detected, and this is matched to the ‘B’. In terms of the rules, ‘B’ is now referred to as ‘V0’. This notation adds the order value to that variable name to avoid potential ambiguities. Both the template, and the equation now match for the ‘)’, except the template also has a ‘:LABEL:REF’. This will allow the term ‘( ~ B )’ to be referenced using the description ‘REF’ within the remainder of the rule execution. At this point, the pattern matcher notices that the template string is exhausted, and as a result concludes there is a match, and this will subsequently lead to the checking of conditions in the rule stage.

The template matcher is not very sophisticated, and is applied to each and every term in the given expression to find all possible matches (See Figure 1.1 Flow Chart for Equation Template Matching below). As this method is explored more deeply in the future, the author hopes that this method of template matching can be improved. At present some cases are difficult to consider, such as if we attempted to refer to the third ‘( ~ D )’ term as being the third of that type, not the fourth in the sequence.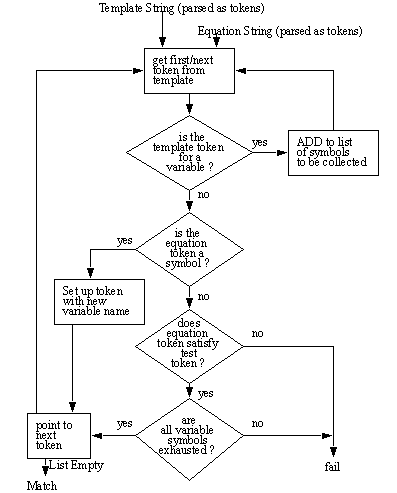

 

Figure 1.1 Flow Chart for Equation Template Matching

After the templates are matched, respective rules are tested for condition satisfaction, then actions are performed if successful.

 

1.3.4 Equation Conditions

It is natural to require some sort of conditions when rules are involved. The question is how to construct these to allow a variety of cases. The direction of this research initially was fairly simplistic, trying to just establish some true or false conditions. This was found to be limiting and as a result there have been a number of functions allowed within the condition matching implementation. These functions are still rather limited, because they do not include some fundamental constructs such as, if, loop, and while statements. Obviously these would be required in a complete system, but for proof of concept, the ramifications of not having these are logically redundant and repetitive condition definitions.

The reader should recall that in the rule file shown in Figure 1.1 Part of a Rule File, the conditions had a few basic types of functions. These include,

COMPARE This directs a comparison of the arguments. If the

comparison is false, a false is returned.

MATH This performs a math operation. Obviously this is false if

the operation cannot be performed.

ASSIGN This will create a variable, and assign a value. There are

no cases at present that make this false.

FIND This will do a complicated lookup from a database or do

some geometrical calculations. This will also act as a catch-

all for all complicated algorithmic calculations. This will

be false if the required ‘FIND’ is not valid, or cannot be done.

These basic operators are some simple ones to start. Eventually these could be expanded to include more elaborate choices, such as loops, ifs, or other valid logical operators. The method for analyzing the condition set is to begin at the top of the set. If any of the conditions become false, then the condition is ruled false. How the false is interpreted is determined by the boolean expression in the rule.

Some details of interest should be identified in the comparison statement. There are a number of basic operators that are intuitively clear, such as <=, >=, <, >. There are other operators that are very specific, for example = is for assignment, whereas == is for a logical equals, and ‘$’ is for existence. There are other operators used in other arguments, but these are considered basic to any reader versed in any computer language.

1.3.5 Rules

These rules are basically production rules. If the conditions are satisfied, then the results are performed. When referring to previous examples the reader will note that a rule only contains two types of entries; ‘EQUATION:’ and ‘RESULT’. The equation section describes the boolean expression that determines if a rule is valid or not. The form of the equation is identical to that given earlier for boolean designs, except that it is limited in operators to AND, OR, and NOT. The arguments of the boolean expression obviously refer to the conditions discussed in the previous section. If the rule passes, then the results indicated in the ‘RESULT:’ lines are executed. If there is more than one, they are applied in sequence from beginning to end. This rules structure is still fairly crude, but it is sufficient to produce a working system. Eventually these could also be augmented with some of the constructs of a modern computer language, to allow compact, and sophisticated result selection.

1.3.6 Results

When setting up the test software originally, the number of result operations was quite conservative. But, as the application grew, it became obvious that many operations were not only desired, but necessary.

When a rule is fired there are a number of expected effects. The first is a change in the ‘state’ of the part. This state change is performed by manipulating the Boolean description of the product, and the sets that the representation refers to. Secondly, these changes must also be accompanied by the addition of steps to the process plan that will eventually be reflected in the final process plan. The manipulation of the equation was fairly straight forward, having only a few fundamental operations.

EQUATION_INSERT_SYMBOL

This will insert a symbol (a set name) at a specified position in an

active expression.

EQUATION_DELETE_SYMBOL

This function will delete a set name that is at a specified location.

EQUATION_DELETE_TERM

A term at a specified location will be deleted.

EQUATION_DELETE_VARIABLE_TERM

This will delete a term that has been given a label using the

‘LABEL’ operator in the template matching string.

EQUATION_INSERT_TERM

A given term will be inserted at the given position in the current

expression.

At present, these few operators seem to perform all operations required for the current template matching methodology. Some notes about the equation manipulation routines are required. First, after a rule result manipulates an equation, the result is stored separately for that operation only. Second, when the result is fired, it refers to a particular term in an expression. This term becomes a sort of root term for reference. So when a rule refers to ‘:’ for example, it is not referring to the main root of the equation, but to the first element in the matched equation. While this may seem somewhat confusing in words, observation of the examples should make the role perfectly clear.

If the equations are being manipulated, it is understandable that the sets the equations represent should also undergo change. This is done through the application of a number of other operators.

COPY_SET

This simply copies one set to a new set.

ADD_SET

This function creates a new set.

ADD_PROPERTY

This function will add a property to a set.

PROPERTY_FUNCTION_VARIABLE

Performs a mathematical operation based on set members.

PROPERTY_FUNCTION_NUMBER

Performs a mathematical operation based on a set member, and a

number.

DELETE_PROPERTY

A specified property will be deleted.

The reader is reminded that these operators are driven by the template matching results in the previous sections. Thus there are references to variable set names, as well as new set names in these functions.

Other functions also exist for a variety of other tasks. These tend to be a bit more complex in requirements. In general these consist of math operations, operation cost reporting, process plan additions, and basic function lookups.

PLAN_PUSH_TEXT

Adds a line of test to the process plan.

PLAN_PUSH_FORMAT

Adds a line of text to the process plan, but using a formatted

output. This allows the use of variables in plan output.

DECLARE_COST

A numerical cost is declared, so that the system may

perform some process selection based upon the cost of operations.

PROPERTY_FUNCTION_VARIABLE

Perform a math function based upon two variable names.

PROPERTY_FUNCTION_NUMBER

Perform a math function on a variable with a number.

FIND

This function allows complicated operations to be performed,

such as the lookup of the cost of a material, or a geometric

property. Many complex functions can be added through this

device.

All of the process plan declarations made are added to a new set. This set is incorporated into the process plan structure using the cost declared as one of the selection functions. Therefore, when a rule result is fired it will declare as much information as possible about the operation that will occur. It can also calculated an estimated cost, and then let the planner know so that it may use the information during selection of the least expensive operation.

1.3.7 Other Considerations for the Rules

These rules are quite specific to the template matching scheme proposed here. More work is required to make this scheme more flexible. Subject to changes that arise from this additional work, it is possible these operators may change slightly or drastically to accommodate the changes.

During the implementation it was noticed that many conditions and other sets were redundant. This was mainly due to the ‘inflexible’ definition of conditions, such as one condition for checking for the existence of the first argument, and a second one for checking for the existence of the second argument. These are identical, except for the variable ‘V0’ as opposed to ‘V1’. This could be easily handled by a variable list for condition calls, to allow one condition check that would easily interchange two arguments in the call stack. This idea may also be expanded to the definition of rules, and results as well.

1.3.8 Structure of the Process Plan

Traditional manufacturing methods tend to separate design and process planning. But, considering the link between design and process planning, it is logical to use a combined representation. In this case the process plan can be viewed as an addition of information to the original design. Most importantly this approach allows the original design to be retained intact, while allowing the process plan to refer to information directly. And, eventually this can be used so that changes to the design are only propagated to the process plan steps that they effect.

A Bill of Material (BOM) list was used as the focus of the process plan. This naturally splits up the design into sub-assemblies and redundant features. So when looking for the design information we look for the ‘main_product’ set type, and when looking for process plans, we look for the ‘MAIN_BOM’ set. In this set there is a list of required parts, and pertinent information, as shown in the example below (This part is covered in detail in Chapter 7, and can be seen in section 7.4).

MAIN_BOM {

ASSEMBLY ( 2.000000 Clip_half Clip_half_OP1 Clip_half_PART )

ASSEMBLY ( 1.000000 0:Logo_Side 0:Logo_Side_OP7 0:Logo_Side_PART)

ASSEMBLY ( 1.000000 Logo_Side Logo_Side_OP13 Logo_Side_PART )

ASSEMBLY ( 1.000000 Spring Spring_OP16 Spring_PART )

ASSEMBLY ( 1.000000 Big_Clothes_Pin Big_Clothes_Pin_OP19

Big_Clothes_Pin_PART )

}

This particular entry contains a total of 5 different parts. At the top of the list are the parts that must be made first. ‘ASSEMBLY’ identifies the parts as members of an assembly, whereas in some cases it may say ‘FEATURE’ to identify the member as a reused feature. The first number in the arguments of these records indicate the quantity of parts required (a real number is used because it is possible to require only a fraction of something). The next item is the name of the part to be produced in the original design. The reader will notice that the second line claims that ‘0:Logo_Side’ is the part to be produced. This notation is used when an assembly is indicated in the design, but it is part of a large equation, and therefore it does not have a distinct name. This particular part is from the part ‘Logo_Side’, and is given the equation location of ‘:0’ in the equation,

( : ( & Clip_half ( ~ Screw_hole );position_screw_hole );add_logo )

And, therefore ‘0:Logo_Side’ is,

( & Clip_half ( ~ Screw_hole );position_screw_hole );add_logo

This notation is not inherently clear, but is necessary to preserve the intent of the designer. The next argument in the list refers to the first operation in the operations list for the part, and the last argument points to a final part state set. For example ‘Spring_OP16’ points to the sets below.

Spring_OP16 {

EQUATION: ( : Spring )

OPERATION ( AND RULE 17:0:0 0.000000 Spring_OP17 spring_ends )

ACTIVE: 0

EXPANDED ( 0 2 3 2 )

}

Spring_OP17 {

DESCRIPTION ( bend spring ends )

DESCRIPTION ( L offset on spring = 0.0 )

DESCRIPTION ( length of free end = 3.400000 )

EQUATION: ( : BEND_SPRING_ENDS_18 )

OPERATION ( AND RULE 18:0:0 0.000000 Spring_OP18 spring_roll )

ACTIVE: 0

EXPANDED ( 0 11 1 0 )

}

BEND_SPRING_ENDS_18 {

form = SPRING

inside_radius = 0.12

outside_radius = 0.2

length = 3.400000

turns = 14.5

rotate_y = 90

offset = 0.0

length = 0.0

}

Spring_OP18 {

DESCRIPTION ( coil spring from wire )

DESCRIPTION ( bend coil spring )

DESCRIPTION ( wire dia. = 0.080000 )

DESCRIPTION ( turns. = 14.500000 )

EQUATION: NULL

}

COIL_SPRING_19 {

wire_dia = 0.080000

turns = 14.500000

}

Spring_PART {

form = COMPLEX

description = Spring

equation = ( : Spring )

}

The reader will notice that there is an equation term in some sets. These equations represent the form of the product after the operation is performed. The possible operations are indicated in the operation fields. The field is easy to interpret. First, the ‘AND’ shown indicates all operations listed are to be done, an ‘OR’ would indicate only one has to be done. The next section is done in anticipation of future development. At present only rules is applied, in the future this would be expanded to include geometrical transformations. ‘RULE’ indicates that the last change was induced by a simple rule selection, and the next field ‘17:0:0’ indicates the applied permutation. The author has noticed that if any search (and planning) methods are to be used, the exact firing conditions must be traceable. Three obvious methods for doing this are by rule number, also by simple geometry matching by equation form (with different variable names), or by matching by analyzing the part fully, and comparing geometry, and other properties. These tasks are without doubt lengthy, but seem to fit cleanly into the proposed framework. The next argument is the cost (estimated) of the operations in question. This slot is filled by the ‘DECLARE_COST’ operator discussed in the last section. These are then used when selecting operations based upon cost.

The end of the ‘OPERATION’ arguments is followed by a pair of arguments. The first one is the subsequent operation, in this case ‘Spring_OP17’ is one of these. Also included is the rule that called for this operation. By also identifying the rule, it can simplify feedback in the case of process plan failure. Although these lists only have one pair of operation/rule, an unlimited list is allowed, this will give the ‘AND’ and ‘OR’ operators some use when selecting alternate and parallel operations.

The reader should note that in ‘Spring_OP17’ there are some ‘DESCRIPTION’ fields. These are used to convey information to the operation planner. In this case ‘DESCRIPTION’ will simply cause the given text to be written directly on the process plan. There are other operators that will be discussed in the operation planning section. The important thing to notice is that all lines in this set are examined by the operation planner, but some are ignored, or not used, such as the ‘EQUATION’ description. The planner keeps track of where it stopped, the operation selected, and failed operations. The ‘ACTIVE’ field will point to the operation that is in use, based upon their order in the set (0 being the first). ‘EXPANDED’ keeps track of the exact state of the planner when it stopped last. This allow the planner to restart from the middle of a search. If for some reason the planner finds an operation that always leads to failure, it will indicate this by adding a ‘FAIL’ to the operation list. Although it is not pictured here, it can be seen in the results section.

As rules are applied and the product description is altered, there are new equations and sets created to accommodate this. One such set is ‘BEND_SPRING_ENDS_18’. For all effective purposes this is equivalent to a design set. And when attempting to backtrack, or examine product geometry at various stages of completion, this provides easy access to all relevant information.

There are some points of interest about this representation. First, the set and operation names are all augmented with numbers (from a global counter) to prevent confusion when set and operation names are reused as the result of rules that are used more than once. This structure is very conducive to replanning and viewing the status of work in process. For example, if a rule for drilling is fired twice, it will result in a duplicate set to keep the drilling operation information in. This obviously causes problems, but by adding a unique number to the name the two sets become different and distinct, while still maintaining a recognizable name.

Finally, a note about the representation in general. The structure described previously can be a bit confusing to deal with, but as the reader will have noticed in the discussion of rule results, and will see in the planning section, these details are buried in the system. The user is not required to deal with these aspects, and therefore the structure given is realistic, and should support planning requirements, without overwhelming the user with complicated data structures.