INTRODUCTIONWhen a phasor transform is applied to a transfer function the result can be expressed as a magnitude and angle that are functions of frequency. The magnitude is the gain, and the angle is the phase shift. In the previous chapter these values were calculated for a single frequency and then multiplied by the input values to get an output value. At different frequencies the transfer function value will change. The transfer function gain and phase angle can be plotted as a function of frequency to give an overall picture of system response. 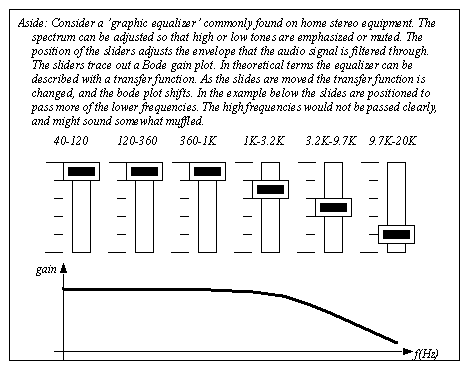
Figure 10.1 Commonly seen Bode plot The mass-spring-damper transfer function from the previous chapter is expanded in Figure 10.2 A phasor transform example. In this example the transfer function is multiplied by the complex conjugate to eliminate the complex number in the denominator. The magnitude of the resulting transfer function is the gain, and the phase shift is the angle. Note that to correct for the quadrant of the phase shift angles pi radians is subtracted for certain frequency values. 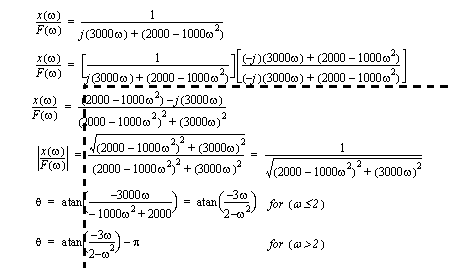
Figure 10.2 A phasor transform example The results in Figure 10.2 A phasor transform example are normally left in variable form so that they may be analyzed for a range of frequencies. An example of this type of analysis is done in Figure 10.3 A phasor transform example (continued). A set of frequencies is used for calculations. These need to be converted from Hz to rad/s before use. For each one of these the gain and phase angle is calculated. The gain gives a ratio between the input sine wave and output sine wave of the system. The magnitude of the output wave can be calculated by multiplying the input wave magnitude by the gain. (Note: recall this example was used in the previous chapter) The phase angle can be added to the input wave to get the phase of the output wave. Gain is normally converted to ’dB’ so that it may cover a larger range of values while still remaining similar numerically. Also note that the frequencies are changed in multiples of tens, or magnitudes. 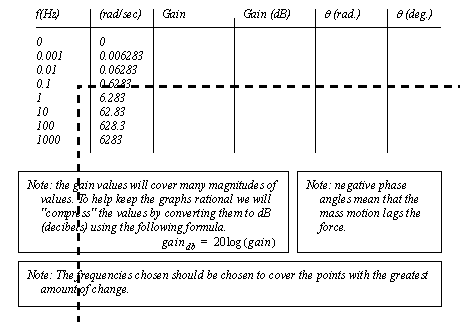
Figure 10.3 A phasor transform example (continued) In this example gain is defined as x/F. Therefore F is the input to the system, and x is the resulting output. The gain means that for each unit of F input to the system, there will be gain*F=x output. If the input and output are sinusoidal, there is a difference in phase between the input and output wave of θ (the phase angle). This is shown in Figure 10.4 A phasor transform example (continued), where an input waveform is supplied with three sinusoidal components. For each of the frequencies a gain and phase shift are calculated. These are then used to calculate the resulting output wave, relative to the input wave. The resulting output represents the steady-state response to the sinusoidal output. 
|