TRANSFER FUNCTIONSTransfer functions are used for equations with one input and one output variable. An example of a transfer function is shown below in Figure 8.1 A transfer function example. The general form calls for output over input on the left hand side. The right hand side is comprised of constants and the ’D’ operator. In the example ’x’ is the output, while ’F’ is the input. 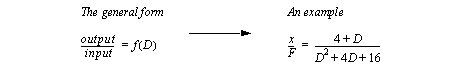
Figure 8.1 A transfer function example If both sides of the example were inverted then the output would become ’F’, and the input ’x’. This ability to invert a transfer function is called reversibility. In reality many systems are not reversible. There is a direct relationship between transfer functions and differential equations. This is shown for the second-order differential equation in Figure 8.2 The relationship between transfer functions and differential equations for a mass-spring-damper example. The homogeneous equation (the left hand side) ends up as the denominator of the transfer function. The non-homogeneous solution ends up as the numerator of the expression. 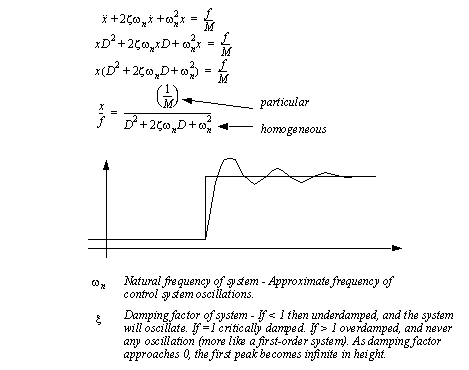
Figure 8.2 The relationship between transfer functions and differential equations for a mass-spring-damper example The transfer function for a first-order differential equation is shown in Figure 8.3 A first-order system response. As before the homogeneous and non-homogeneous parts of the equation becomes the denominator and the numerator of the transfer function. 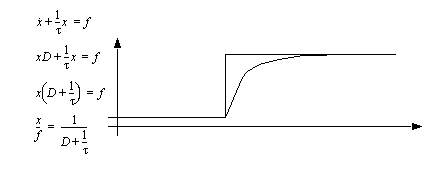
|