EXAMPLE SYSTEMSThe list of instructions below can be useful when approaching a circuits problem. The most important concept to remember is that a minute of thinking about the solution approach will save ten minutes of backtracking and fixing mistakes. 1. Look at the circuit to determine if it is a standard circuit type such as a voltage divider, current divider or an op-amp inverting amplifier. If so, use the standard solution to solve the problem. 2. Otherwise, consider the nodes and loops in the circuit. If the circuit contains fewer loops, select the current loop method. If the circuit contains fewer nodes, select the node voltage method. Before continuing, verify that the select method can be used for the circuit. 3. For the node voltage method define node voltages and current directions. For the current loop method define current loops and indicate voltage rises or drops by adding ’+’ or ’-’ signs. 4. Write the equations for the loops or nodes. 5. Identify the desired value and eliminate unwanted values using algebra techniques. 6. Use numerical values to find a final answer. 
The circuit in Figure 7.22 Example problem could be solved with two loops, or two nodes. An arbitrary decision is made to use the current loop method. The voltages around each loop are summed to provide equations for each loop. 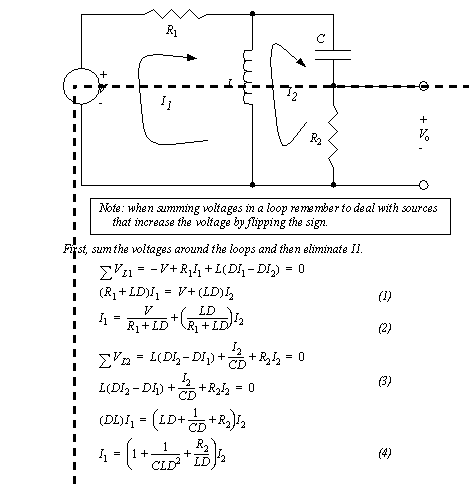
The equations in Figure 7.22 Example problem are manipulated further in Figure 7.23 Example problem (continued) to develop an input-output equation for the second current loop. This current can be used to find the current through the output resistor R2. The output voltage can then be found by multiplying the R2 and I2. 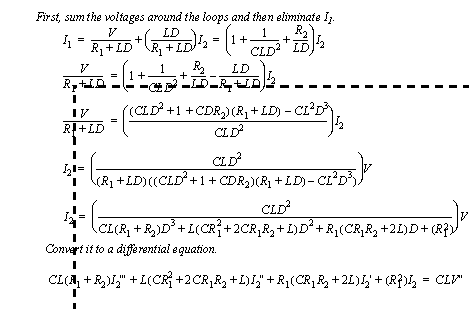
Figure 7.23 Example problem (continued) The equations can also be manipulated into state equations, as shown in Figure 7.24 Example problem (continued). In this case a dummy variable is required to replace the two first derivatives in the first equation. The dummy variable is used in place of I1, which now becomes an output variable. In the remaining state equations I1 is replaced by q1. In the final matrix form the state equations are in one matrix, and the output variable must be calculated separately. 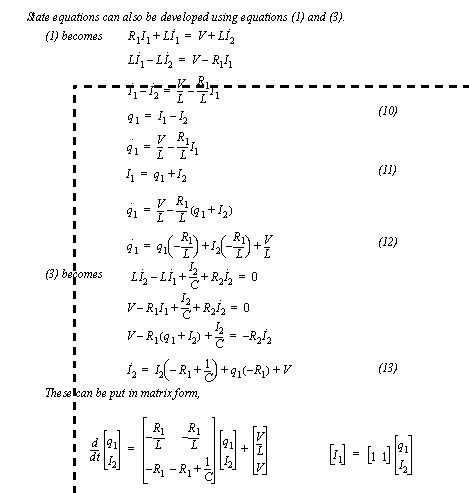
Figure 7.24 Example problem (continued) 
Figure 7.25 Drill problem: Use the node voltage method 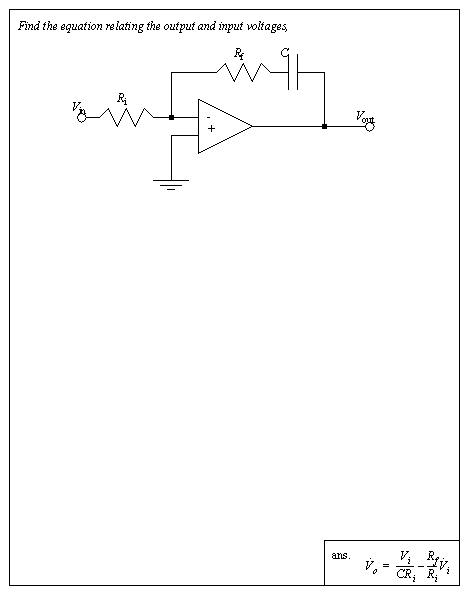
Figure 7.26 Drill problem: Find the state equation The circuit in Figure 7.27 Circuit solution using impedances can be evaluated as a voltage divider when the capacitor is represented as an impedance. In this case the result is a first-order differential equation. 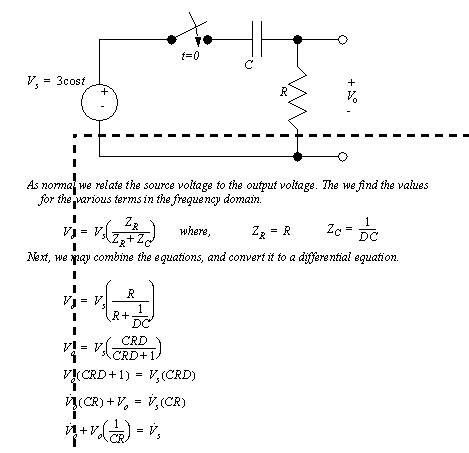
Figure 7.27 Circuit solution using impedances The first-order differential equation in Figure 7.27 Circuit solution using impedances is continued in Figure 7.28 Circuit solution using impedances (continued) where the equation is integrated. The solution is left in variable form, except for the supply voltage. 
|