INPUT-OUTPUT EQUATIONS

A typical system will be described by more than one differential equation. These equations can be solved to find a single differential equation that can then be integrated. The basic technique is to arrange the equations into an input-output form, such as that in Figure 6.5 Developing input-output equations. These equations will have only a single output variable, and these are always shown on the left hand side. The input variables (there can be more than one) are all on the right hand side of the equation, and act as the non-homogeneous forcing function.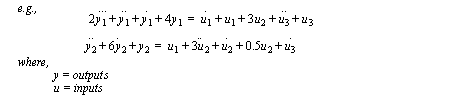

 

Figure 6.5 Developing input-output equations

A sample derivation of an input-output equation from a system of differential equations is given in Figure 6.6 Example: An input output equation. This begins by replacing the differential operator and combining the equations to eliminate one of the output variables. The solution ends by rearranging the equation to input-output form.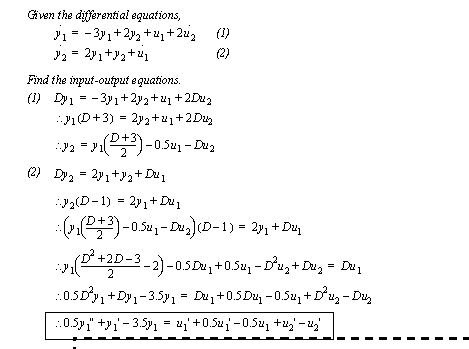

 

Figure 6.6 Example: An input output equation

 

Figure 6.7 Drill problem: Find the second equation in the previous example

In some instances we will want to numerically integrate an input-output equation. The example starting in Figure 6.8 Example: Writing an input-output equation as a differential equation shows the development of an input-output equation for two freely rolling masses joined by a spring. The final equation has a derivative on the right hand side that would prevent it from being analyzed in many cases. In particular if the input force ’F’ was a step function the first derivative would yield an undefined (infinite) value that could not be integrated.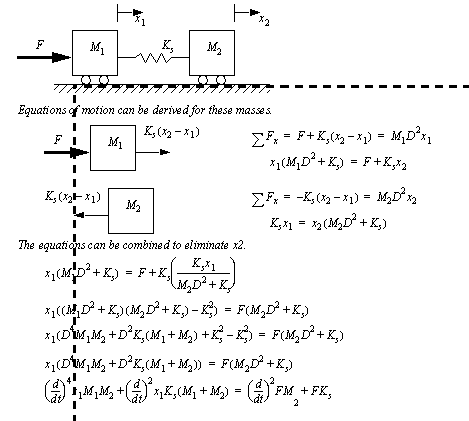

 

Figure 6.8 Example: Writing an input-output equation as a differential equation

The equation is then converted to state variable form, including a step to calculate a second derivative of the input, as shown in Figure 6.9 Example: Writing state equations for equations with derivatives.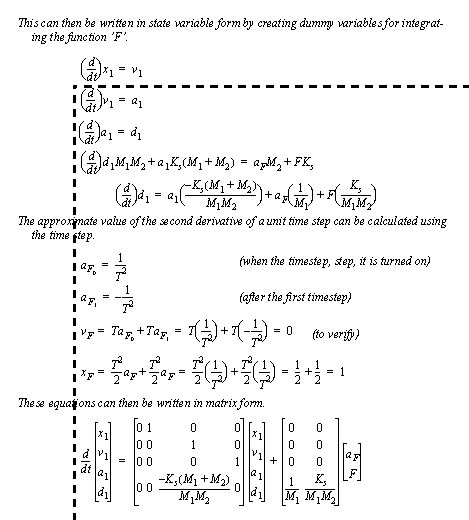

 

Figure 6.9 Example: Writing state equations for equations with derivatives