THE DIFFERENTIAL OPERATORThe differential operator ’d/dt’ can be written in a number of forms. In this book there have been two forms used thus far, d/dt x and x-dot. For convenience we will add a third, ’D’. The basic definition of this operator, and related operations are shown in Figure 6.1 General properties of the differential operator. In basic terms the operator can be manipulated as if it is a normal variable. Multiplying by ’D’ results in a derivative, dividing by ’D’ results in an integral. The first-order axiom can be used to help solve a first-order differential equation. 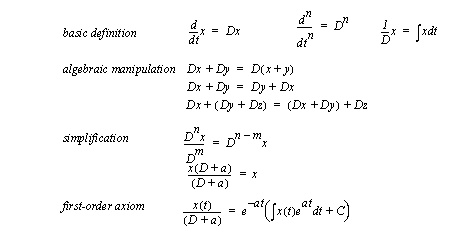
Figure 6.1 General properties of the differential operator 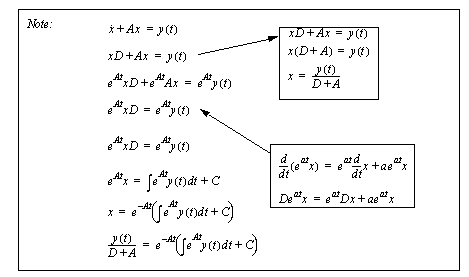
Figure 6.2 Proof of the first-order axiom Figure 6.3 Example: A simplification with the differential operator contains an example of the manipulation of a differential equation using the ’D’ operator. The solution begins by replacing the ’d/dt’ terms with the ’D’ operator. After this the equation is rearranged to simplify the expression. Notice that the manipulation follows the normal rules of algebra. 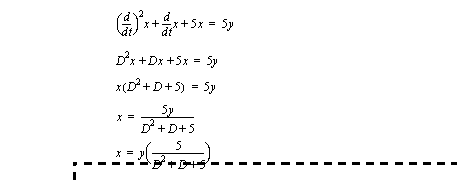
Figure 6.3 Example: A simplification with the differential operator An example of the solution of a first-order differential equation is given in Figure 6.4 Example: A a solution for a first-order system. This begins by replacing the differential operator and rearranging the equation. The first-order axiom is then used to obtain the solution. The initial conditions are then used to calculate the coefficient values. 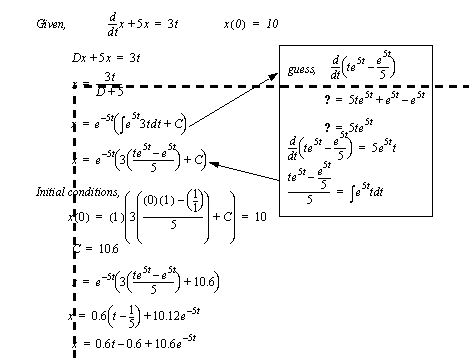
|