DESIGN CASEA large machine is to be driven by a permanent magnet electric motor. A 20:1 gear box is used to reduce the speed and increase the torque of the motor. The motor drives a 10000kg mass in translation through a rack and pinion gear set. The pinion has a pitch diameter of 6 inches. A 10 foot long shaft is required between the gear box and the rack and pinion set. The mass moves on rails with static and dynamic coefficients of friction of 0.2 and 0.1 respectively. We want to select a shaft diameter that will keep the system critically damped when a voltage step input of 20V is applied to the motor. To begin the analysis the velocity curve in Figure 5.28 Example: Motor speed curve and the derived differential equation was obtained experimentally by applying a voltage of 15V to the motor with no load attached. In addition the resistance of the motor coils was measured and found to be 40 ohms. The steady-state speed and time constant were used to determine the constants for the motor. 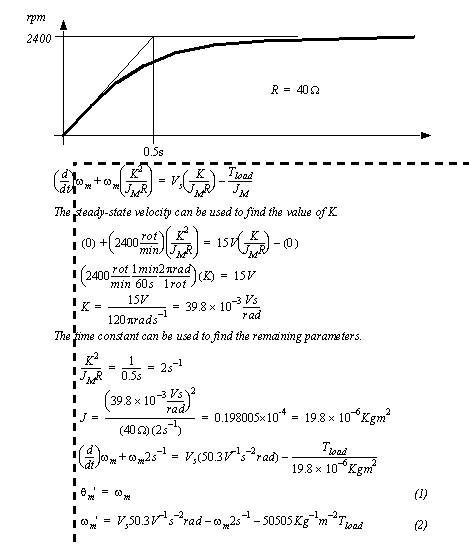
Figure 5.28 Example: Motor speed curve and the derived differential equation The remaining equations describing the system are developed in Figure 5.29 Example: Additional equations to model the machine. These calculations are done with the assumption that the inertial effects of the gears and other components are insignificant. 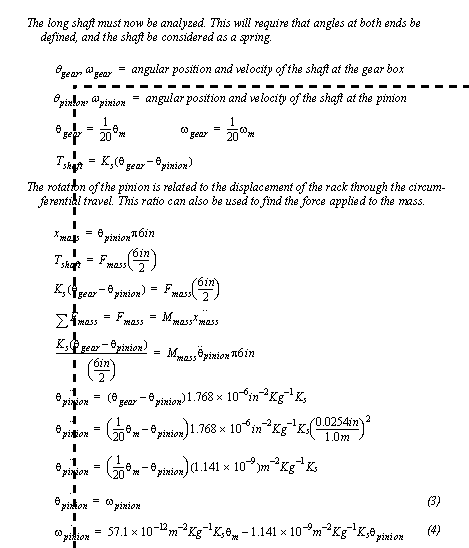
Figure 5.29 Example: Additional equations to model the machine If the gear box is assumed to have relatively small moment of inertia, then we can say that the torque load on the motor is equal to the torque in the shaft. This then allows the equation for the motor shaft to be put into a useful form, as shown in Figure 5.30 Example: Numerical analysis of system response. Having this differential equation now allows the numerical analysis to proceed. The analysis involves iteratively solving the equations and determining the point at which the system begins to overshoot, indicating critical damping. 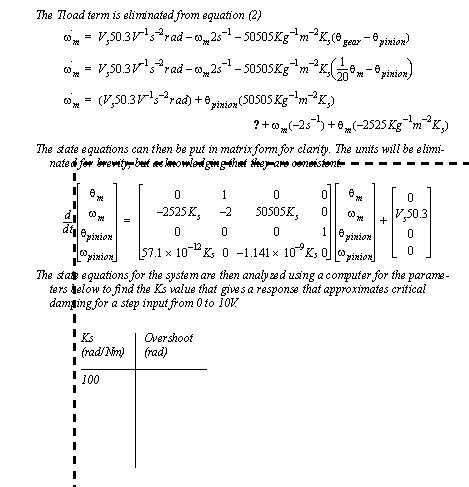
Figure 5.30 Example: Numerical analysis of system response These results indicate that a spring value of XXX is required to have the system behave as if it is critically damped. (Note: Clearly this system is not second order, but in the absence of another characteristics we approximate it as second order.) |