MODELINGFree Body Diagrams (FBDs) are required when analyzing rotational systems, as they were for translating systems. The force components normally considered in a rotational system include, • inertia - opposes acceleration and deceleration • levers - rotate small angles • gears and belts - change rotational speeds and torques 5.2.1 InertiaWhen unbalanced torques are applied to a mass it will begin to accelerate, in rotation. The sum of applied torques is equal to the inertia forces shown in Figure 5.3 Summing moments and angular inertia. 
Figure 5.3 Summing moments and angular inertia The mass moment of inertia determines the resistance to acceleration. This can be calculated using integration, or found in tables. When dealing with rotational acceleration it is important to use the mass moment of inertia, not the area moment of inertia. The center of rotation for free body rotation will be the centroid. Moment of inertia values are typically calculated about the centroid. If the object is constrained to rotate about some point, other than the centroid, the moment of inertia value must be recalculated. The parallel axis theorem provides the method to shift a moment of inertia from a centroid to an arbitrary center of rotation, as shown in Figure 5.4 Parallel axis theorem for shifting a mass moment of inertia. 
Figure 5.4 Parallel axis theorem for shifting a mass moment of inertia 
Figure 5.5 Parallel axis theorem for shifting a area moment of inertia 
An example of calculating a mass moment of inertia is shown in Figure 5.6 Example: Mass moment of inertia. In this problem the density of the material is calculated for use in the integrals. The integrals are then developed using slices for the integration element dM. The integrals for the moments about the x and y axes, are then added to give the polar moment of inertia. This is then shifted from the centroid to the new axis using the parallel axis theorem. 
Figure 5.6 Example: Mass moment of inertia 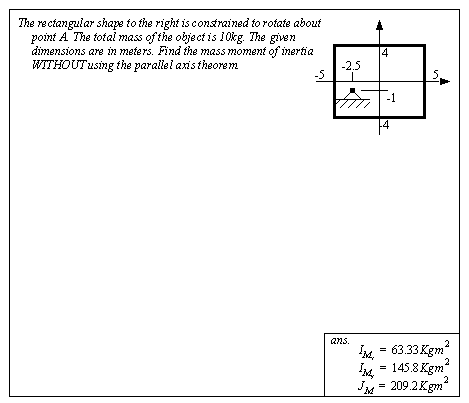
Figure 5.7 Drill problem: Mass moment of inertia calculation 
Figure 5.8 Drill problem: Find the velocity of the rotating shaft 5.2.2 SpringsTwisting a rotational spring will produce an opposing torque. This torque increases as the deformation increases. A simple example of a solid rod torsional spring is shown in Figure 5.9 A solid torsional spring. The angle of rotation is determined by the applied torque, T, the shear modulus, G, the area moment of inertia, JA, and the length, L, of the rod. The constant parameters can be lumped into a single spring coefficient similar to that used for translational springs. 
Figure 5.9 A solid torsional spring The spring constant for a torsional spring will be relatively constant, unless the material is deformed outside the linear elastic range, or the geometry of the spring changes significantly. When dealing with strength of material properties the area moment of inertia is required. The calculation for the area moment of inertia is similar to that for the mass moment of inertia. An example of calculating the area moment of inertia is shown in Figure 5.10 Example: Area moment of inertia, and based on the previous example in Figure 5.6 Example: Mass moment of inertia. The calculations are similar to those for the mass moments of inertia, except for the formulation of the integration elements. Note the difference between the mass moment of inertia and area moment of inertia for the part. The area moment of inertia can be converted to a mass moment of inertia simply by multiplying by the density. Also note the units. 
Figure 5.10 Example: Area moment of inertia 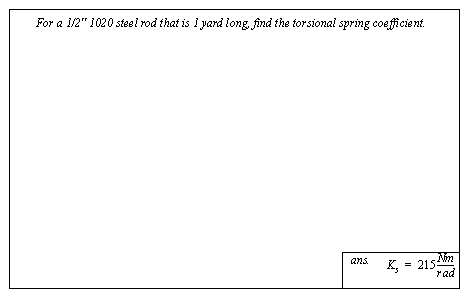
Figure 5.11 Drill problem: Find the torsional spring coefficient An example problem with torsional springs is shown in Figure 5.12 Example: A rotational spring. There are three torsional springs between two rotating masses. The right hand spring is anchored solidly in a wall, and will not move. A torque is applied to the left hand spring. Because the torsional spring is considered massless the torque will be the same at the other end of the spring, at mass J1. FBDs are drawn for both of the masses, and forces are summed. (Note: the similarity in the methods used for torsional, and for translational springs.) These equations are then rearranged into state variable equations, and finally put in matrix form. 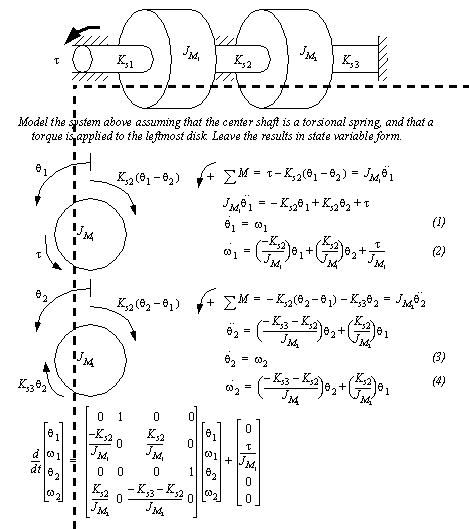
Figure 5.12 Example: A rotational spring 5.2.3 DampingRotational damping is normally caused by viscous fluids, such as oils, used for lubrication. It opposes angular velocity with the relationships shown in Figure 5.13 The rotational damping equation. The first equation is used for a system with one rotating and one stationary part. The second equation is used for damping between two rotating parts. 
Figure 5.13 The rotational damping equation 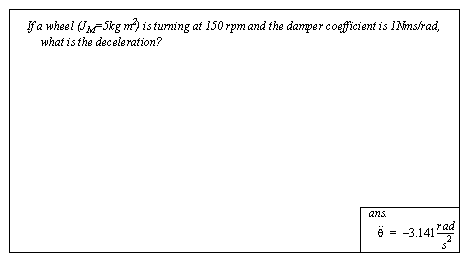
Figure 5.14 Drill problem: Find the deceleration The example in Figure 5.12 Example: A rotational spring is extended to include damping in Figure 5.15 Exampl: A torsional mass spring damper ystem. The primary addition from the previous example is the addition of the damping forces to the FBDs. In this case the damper coefficients are indicated with ’B’, but ’Kd’ could have also been used. The state equations were developed in matrix form. Visual comparison of the final matrices in this and the previous example reveal that the damping terms are the only addition. 
Figure 5.15 Exampl: A torsional mass spring damper ystem 5.2.4 LeversThe lever shown in Figure 5.16 Force transmission with a level can be used to amplify forces or motion. Although theoretically a lever arm could rotate fully, it typically has a limited range of motion. The amplification is determined by the ratio of arm lengths to the left and right of the center. 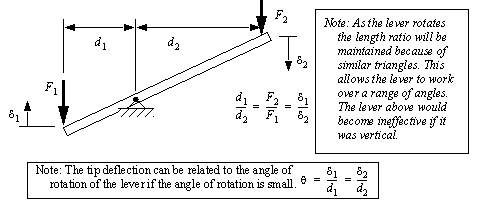
Figure 5.16 Force transmission with a level 
Figure 5.17 Drill problem: Find the required force 5.2.5 Gears and BeltsWhile levers amplify forces and motions over limited ranges of motion, gears can rotate indefinitely. Some of the basic gear forms are listed below. Spur - Round gears with teeth parallel to the rotational axis. Rack - A straight gear (used with a small round gear called a pinion). Helical - The teeth follow a helix around the rotational axis. Bevel - The gear has a conical shape, allowing forces to be transmitted at angles. Gear teeth are carefully designed so that they will mesh smoothly as the gears rotate. The forces on gears acts at a tangential distance from the center of rotation called the pitch diameter. The ratio of motions and forces through a pair of gears is proportional to their radii, as shown in Figure 5.18 Basic Gear Relationships. The number of teeth on a gear is proportional to the diameter. The gear ratio is used to measure the relative rotations of the shafts. For example a gear ratio of 20:1 would mean the input shaft of the gear box would have to rotate 20 times for the output shaft to rotate once. 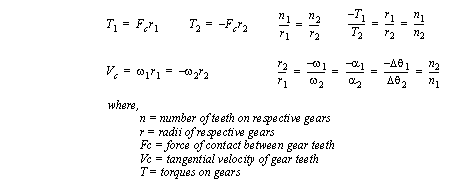
Figure 5.18 Basic Gear Relationships For lower gear ratios a simple gear box with two gears can be constructed. For higher gear ratios more gears can be added. To do this, compound gear sets are required. In a compound gear set two or more gears are connected on a single shaft, as shown in Figure 5.19 Example: A compound gear set. In this example the gear ratio on the left is 4:1, and the ratio for the set on the right is 4:1. Together they give a gear ratio of 16:1. 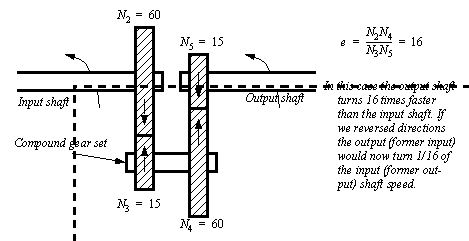
Figure 5.19 Example: A compound gear set A manual transmission is shown in Figure 5.20 Example: A manual transmission. In the transmission the gear ratio is changed by sliding (left-right) some of the gears to change the sequence of gears transmitting the force. Notice that when in reverse an additional compound gear set is added to reverse the direction of rotation. 
Figure 5.20 Example: A manual transmission Rack and pinion gear sets are used for converting rotation to translation. A rack is a long straight gear that is driven by a small mating gear called a pinion. The basic relationships are shown in Figure 5.21 Relationships for a rack and pinion gear set. 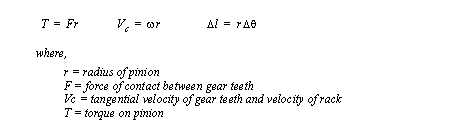
Figure 5.21 Relationships for a rack and pinion gear set Belt based systems can be analyzed with methods similar to gears (with the exception of teeth). A belt wound around a drum will act like a rack and pinion gear pair. A belt around two or more pulleys will act like gears. 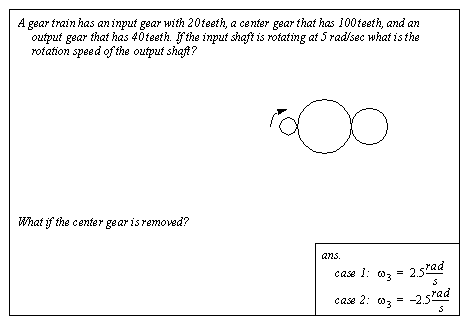
Figure 5.22 Drill problem: Find the gear speed 5.2.6 FrictionFriction between rotating components is a major source of inefficiency in machines. It is the result of contact surface materials and geometries. Calculating friction values in rotating systems is more difficult than translating systems. Normally rotational friction will be given as static and kinetic friction torques. An example problem with rotational friction is shown in Figure 5.23 Example: A system with friction. Basically these problems require that the model be analyzed as if the friction surface is fixed. If the friction force exceeds the maximum static friction the mechanism is then analyzed using the dynamic friction torque. There is friction between the shaft and the hole in the wall. The friction force is left as a variable for the derivation of the state equations. The friction value must be calculated using the appropriate state equation. The result of this calculation and the previous static or dynamic condition is then used to determine the new friction value. 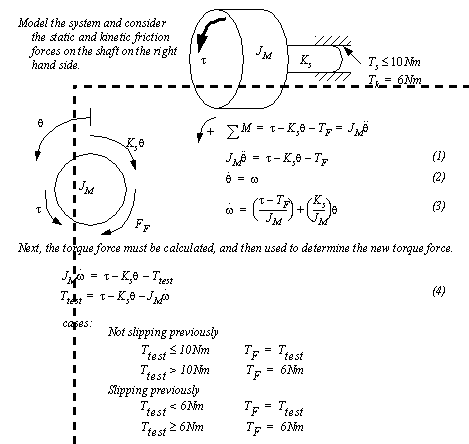
Figure 5.23 Example: A system with friction The friction example in Figure 5.23 Example: A system with friction can be analyzed using the C program in Figure 5.24 Example: A C program for the friction example in Figure 5.23. For the purposes of the example some component values are selected and the system is assumed to be at rest initially. The program loops to integrate the state equations. Each loop the friction conditions are checked and then used for a first-order solution to the state equations. 
Figure 5.24 Example: A C program for the friction example in Figure 5.23 Example: A system with friction 5.2.7 Permanent Magnet Electric MotorsDC motors create a torque between the rotor (inside) and stator (outside) that is related to the applied voltage or current. In a permanent magnet motor there are magnets mounted on the stator, while the rotor consists of wound coils. When a voltage is applied to the coils the motor will accelerate. The differential equation for a motor is shown in Figure 5.25 Model of a permanent magnet DC motor, and will be derived in a later chapter. The value of the constant ’K’ is a function of the motor design and will remain fixed. The value of the coil resistance ’R’ can be directly measured from the motor. The moment of inertia ’J’ should include the motor shaft, but when a load is added this should be added to the value of ’J’. 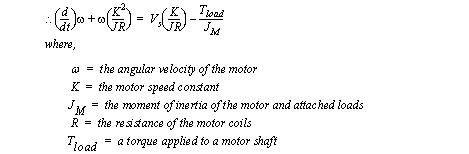
Figure 5.25 Model of a permanent magnet DC motor The speed response of a permanent magnet DC motor is first-order. The steady-state velocity will be a straight line function of the torque applied to the motor, as shown in Figure 5.26 Torque speed curve for a permanent magnet DC motor. In addition the line shifts outwards as the voltage applied to the motor increases. 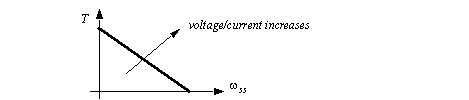
Figure 5.26 Torque speed curve for a permanent magnet DC motor |