When doing experiments, data is often collected in the form of individual data points (not as complete functions). It is often necessary to integrate or differentiate these values. The basic equations for integrating and differentiating are shown in Figure 4.30 Example: Integration and differentiation using data points. Given data points, y, collected at given times, t, we can integrate and differentiate using the given equations. The integral is basically the average height of the two points multiplied by the width to give an area, or integral. The first derivative is basically the slope between two points. The second derivative is the change in slope values for three points. In a computer based system the time points are often equally spaced in time, so the difference in time can be replaced with a sample period, T. Ideally the time steps would be as small as possible to increase the accuracy of the estimates.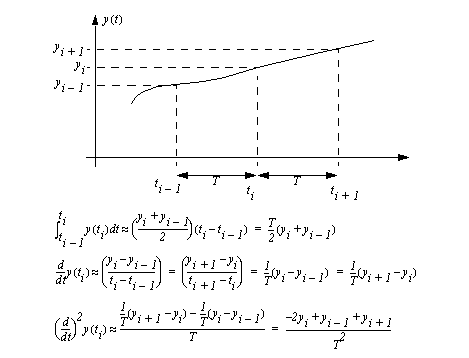
Figure 4.30 Example: Integration and differentiation using data points
An example of numerical integration using Scilab is given in Figure 4.31 Example: Integration with a Scilab program and Figure 4.32 Example: Integration with a Scilab Program (cont’d).
Figure 4.31 Example: Integration with a Scilab program
Figure 4.32 Example: Integration with a Scilab Program (cont’d)