EXPLICIT SOLUTIONSSolving a differential equation results in an explicit solution. This equation provides the general response as a function of time, but it can also be used to find frequencies and other characteristics of interest. This section will review techniques used to integrate first and second-order homogenous differential equations. These equations correspond to systems without inputs, also called unforced systems. Non-homogeneous differential equations will also be reviewed. The basic types of differential equations are shown in Figure 3.2 Standard equation forms. Each of these equations is linear. On the left hand side is the integration variable ’x’. If the right hand side is zero, then the equation is homogeneous. Each of these equations is linear because each of the terms on the left hand side is simply multiplied by a linear coefficient. 
Figure 3.2 Standard equation forms A general solution for a first-order homogeneous differential equation is given in Figure 3.3 Example: General solution of a first-order homogeneous equation. The solution begins with the solution of the homogeneous equation where a general form is ’guessed’. Substitution leads to finding the value of the coefficient ’Y’. Following this, the initial conditions for the equation are used to find the value of the coefficient ’X’. Notice that the final equation will begin at the initial displacement, but approach zero as time goes to infinity. The e-to-the-x behavior is characteristic for a first-order response. 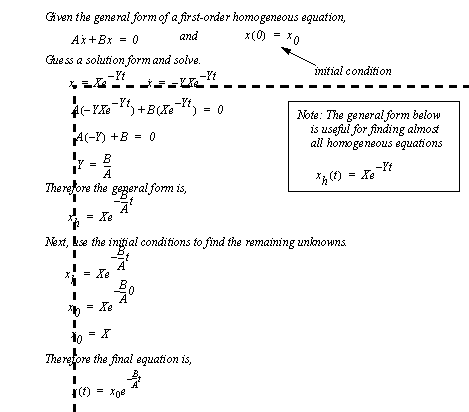
Figure 3.3 Example: General solution of a first-order homogeneous equation 
Figure 3.4 Drill problem: First order homogeneous differential equation The general solution to a second-order homogeneous equation is shown in Figure 3.5 Example: Solution of a second-order homogeneous equation. The solution begins with a guess of the homogeneous solution, and the solution of a quadratic equation. There are three possible cases that result from the solution of the quadratic equation: different but real roots; two identical real roots; or two complex roots. The three cases result in three different forms of solutions, as shown. The complex result is the most notable because it results in sinusoidal oscillations. It is not shown, but after the homogeneous solution has been found, the initial conditions need to be used to find the remaining coefficient values. As mentioned above, a complex solution when solving the homogeneous equation results in a sinusoidal oscillation, as proven in Figure 3.6 Example: Phase shift solution for a second-order homogeneous differential equation. The most notable part of the solution is that there is both a frequency of oscillation and a phase shift. This form is very useful for analyzing the frequency response of a system, as will be seen in a later chapter. 
Figure 3.5 Example: Solution of a second-order homogeneous equation 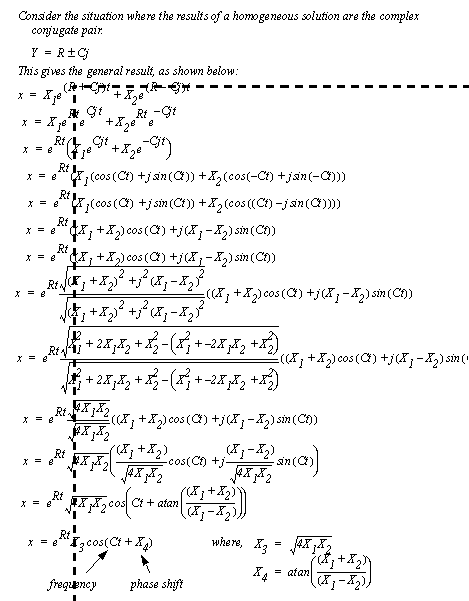
Figure 3.6 Example: Phase shift solution for a second-order homogeneous differential equation 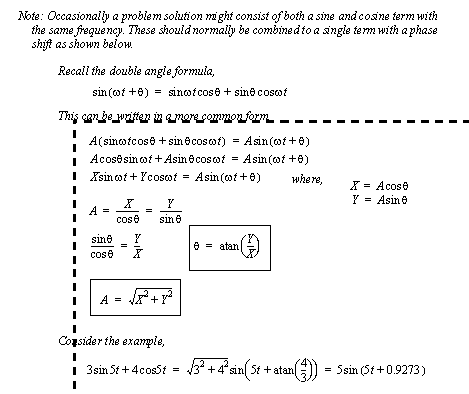
Figure 3.7 Example: Phase shift solution form 
Figure 3.8 Drill problem: Second order homogeneous differential equation The methods for solving non-homogeneous differential equations builds upon the methods used for the solution of homogeneous equations. This process adds a step to find the particular solution of the equation. An example of the solution of a first-order non-homogeneous equation is shown in Figure 3.9 Example: Solution of a first-order non-homogeneous equation. To find the homogeneous solution the non-homogeneous part of the equation is set to zero. To find the particular solution the final form must be guessed. This is then substituted into the equation, and the values of the coefficients are found. Finally the homogeneous and particular solutions are added to get the final equation. The overall response of the system can be obtained by adding the homogeneous and particular parts. This is acceptable because the equations are linear, and the principle of superposition applies. The homogeneous equation deals with the response to initial conditions, and the particular solution deals with the response to forced inputs. 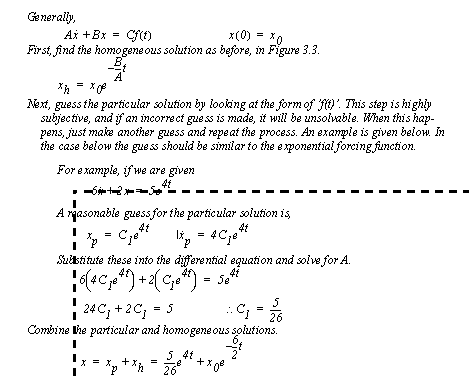
Figure 3.9 Example: Solution of a first-order non-homogeneous equation The method for finding a particular solution for a second-order non-homogeneous differential equation is shown in Figure 3.10 Example: Solution of a second-order non-homogeneous equation. In this example the forcing function is sinusoidal, so the particular result should also be sinusoidal. The final result is converted into a phase shift form. 
Figure 3.10 Example: Solution of a second-order non-homogeneous equation When guessing particular solutions, the forms in Figure 3.11 General forms for particular solutions can be helpful. 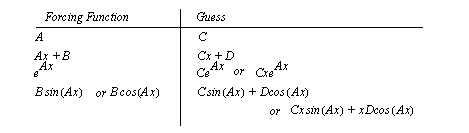
Figure 3.11 General forms for particular solutions 
Figure 3.12 Drill problem: Second order non-homogeneous differential equation An example of a second-order system is shown in Figure 3.13 Example: Second-order system. As expected, it begins with a FBD and summation of forces. This is followed with the general solution of the homogeneous equation. Real roots are assumed thus allowing the problem solution to continue in Figure 3.14 Example: Second-order system (continued). 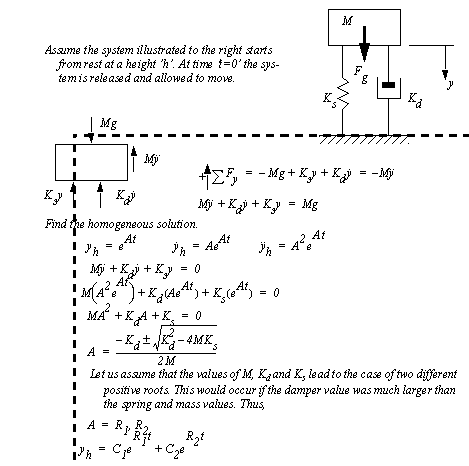
Figure 3.13 Example: Second-order system The solution continues by assuming a particular solution and calculating values for the coefficients using the initial conditions in Figure 3.14 Example: Second-order system (continued). The final result is a second-order system that is overdamped, with no oscillation. 
Figure 3.14 Example: Second-order system (continued) 
|