FINDING OUTPUT EQUATIONSAn input to a system is normally expressed as a function of time that can be converted to the s-domain. An example of this conversion for a step function is shown in Figure 17.16 An input function. 
Figure 17.16 An input function In the previous section we converted differential equations, for systems, to transfer functions in the s-domain. These transfer functions are a ratio of output divided by input. If the transfer function is multiplied by the input function, both in the s-domain, the result is the system output in the s-domain. 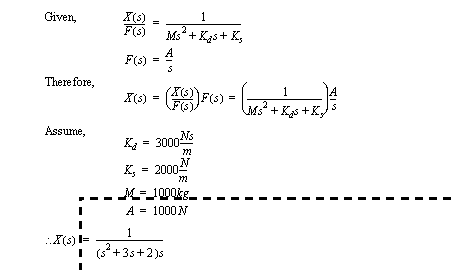
Figure 17.17 A transfer function multiplied by the input function Output functions normally have complex forms that are not found directly in transform tables. It is often necessary to simplify the output function before it can be converted back to the time domain. Partial fraction methods allow the functions to be broken into smaller, simpler components. The previous example in Figure 17.17 A transfer function multiplied by the input function is continued in Figure 17.18 Partial fractions to reduce an output function using a partial fraction expansion. In this example the roots of the third order denominator polynomial, are calculated. These provide three partial fraction terms. The residues (numerators) of the partial fraction terms must still be calculated. The example shows a method for finding resides by multiplying the output function by a root term, and then finding the limit as s approaches the root. 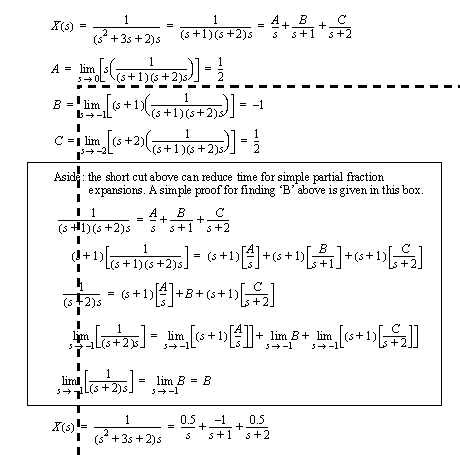
Figure 17.18 Partial fractions to reduce an output function After simplification with partial fraction expansion, the output function is easily converted back to a function of time as shown in Figure 17.19 Partial fractions to reduce an output function (continued). 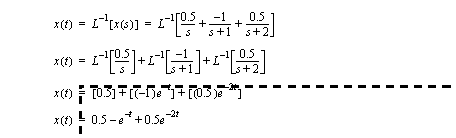
Figure 17.19 Partial fractions to reduce an output function (continued) |