MODELING TRANSFER FUNCTIONS IN THE s-DOMAINIn previous chapters differential equations, and then transfer functions, were derived for mechanical and electrical systems. These can be converted to the s-domain, as shown in the mass-spring-damper example in Figure 17.12 A mass-spring-damper example. In this case we assume the system starts undeflected and at rest, so the ’D’ operator may be directly replaced with the Laplace ’s’. If the system did not start at rest and undeflected, the ’D’ operator would be replaced with a more complex expression that includes the initial conditions. 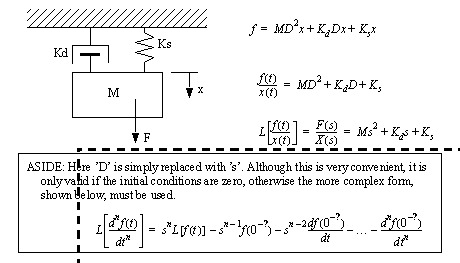
Figure 17.12 A mass-spring-damper example Impedances in the s-domain are shown in Figure 17.13 Impedances of electrical components. As before these assume that the system starts undeflected and at rest. 
Figure 17.13 Impedances of electrical components Figure 17.14 A circuit example shows an example of circuit analysis using Laplace transforms. The circuit is analyzed as a voltage divider, using the impedances of the devices. The switch that closes at t=0s ensures that the circuit starts at rest. The calculation result is a transfer function. 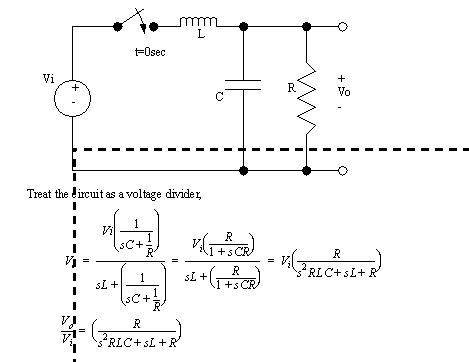
Figure 17.14 A circuit example At this point two transfer functions have been derived. To state the obvious, these relate an output and an input. To find an output response, an input is needed. 
|