INTRODUCTIONLaplace transforms provide a method for representing and analyzing linear systems using algebraic methods. In systems that begin undeflected and at rest the Laplace ’s’ can directly replace the d/dt operator in differential equations. It is a superset of the phasor representation in that it has both a complex part, for the steady state response, but also a real part, representing the transient part. As with the other representations the Laplace s is related to the rate of change in the system. 
The basic definition of the Laplace transform is shown in Figure 17.2 The Laplace transform. The normal convention is to show the function of time with a lower case letter, while the same function in the s-domain is shown in upper case. Another useful observation is that the transform starts at t=0s. Examples of the application of the transform are shown in Figure 17.3 Proof of the step function transform for a step function and in Figure 17.4 Proof of the first order derivative transform for a first order derivative. 
Figure 17.2 The Laplace transform 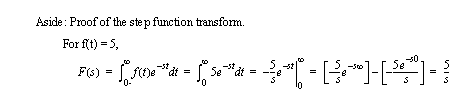
Figure 17.3 Proof of the step function transform 
Figure 17.4 Proof of the first order derivative transform The previous proofs were presented to establish the theoretical basis for this method, however tables of values will be presented in a later section for the most popular transforms. |