SYSTEM EXAMPLESAn orderly approach to system analysis can simplify the process of analyzing large systems. The list of steps below is based on general observations of good problem solving techniques. 1. Assign letters/numbers to designate force components (if not already done) - this will allow you to refer to components in your calculations. 2. Define positions and directions for any moving masses. This should include the selection of reference points. 3. Draw free body diagrams for each component, and add forces (inertia is optional). 4. Write equations for each component by summing forces. 5.(next chapter) Combine the equations by eliminating unwanted variables. 6.(next chapter) Develop a final equation that relates input (forcing functions) to outputs (results). 
Consider the cart in Figure 2.29 Example: A simple translational system. On the left is a force, it is opposed by a spring and damper on the right. The basic problem definition already contains all of the needed definitions, so no others are required. The FBD for the mass shows the applied force and the reaction forces from the spring and damper. When the forces are summed the inertia is on the right side of the equation in Newton’s form. This equation is then rearranged to a second-order non-homogeneous differential equation. 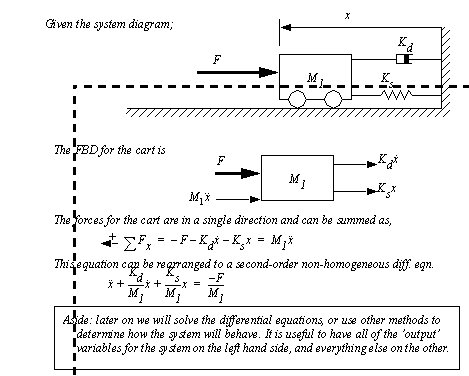
Figure 2.29 Example: A simple translational system 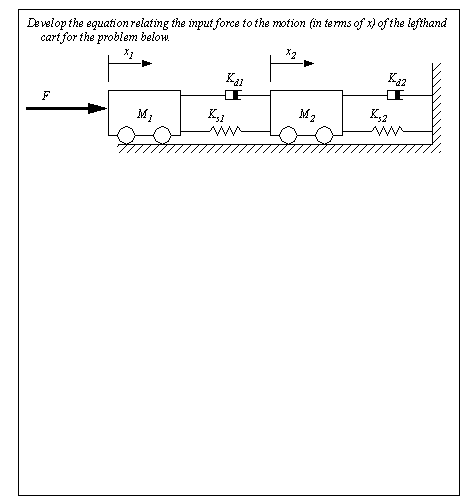
Figure 2.30 Drill problem: Find the differential equations A simplified model of an elevator (M1) and a passenger (M2) are shown in Figure 2.31 Example: A multi-body translating system (an elevator with a passenger). In this example many of the required variables need to be defined. These are added to the FBDs. Care is also taken to ensure that all forces between bodies are equal in magnitude, but opposite in direction. The wall forces are ignored because they are statically indeterminate, and x-axis force components are irrelevant to the forces in the y-axis. 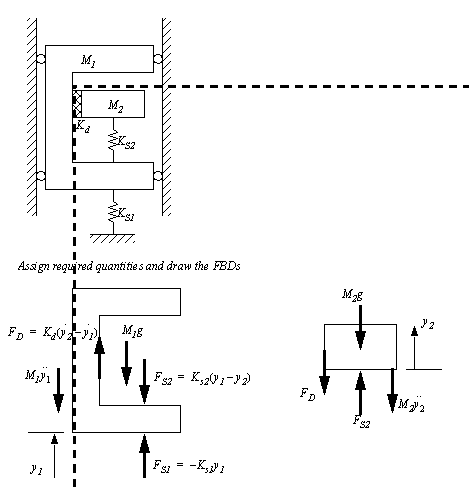
Figure 2.31 Example: A multi-body translating system (an elevator with a passenger) The forces on the FBDs are summed and the equations are expanded in Figure 2.32 Example: Equations for the elevator. 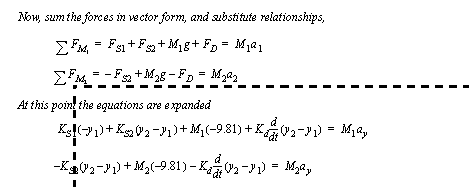
Figure 2.32 Example: Equations for the elevator 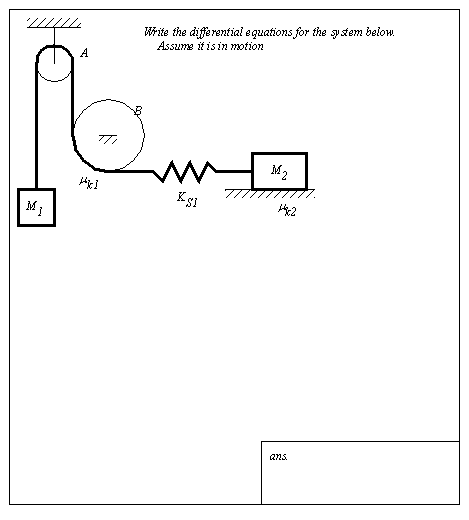
Figure 2.33 Drill problem: A more complex translational systems Consider the springs shown in Figure 2.34 Springs in parallel and series (kinematically). When two springs are combined in this manner they can be replaced with a single equivalent spring. In the parallel spring combination the overall stiffness of the spring would increase. In the series spring combination the overall stiffness would decrease. 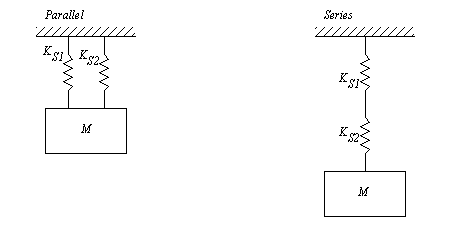
Figure 2.34 Springs in parallel and series (kinematically) Figure 2.35 Example: Calculation of an equivalent spring coefficient for springs in series shows the calculations required to find a spring coefficient equivalent to the two springs in series. The first step is to draw a FBD for the mass at the bottom, and for a point between the two springs, P. The forces for both of these are then summed. The next process is to combine the two equations to eliminate the height variable created for point P. After this, the equation is rearranged into Hooke’s law, and the equivalent spring coefficient is found. 
Figure 2.35 Example: Calculation of an equivalent spring coefficient for springs in series 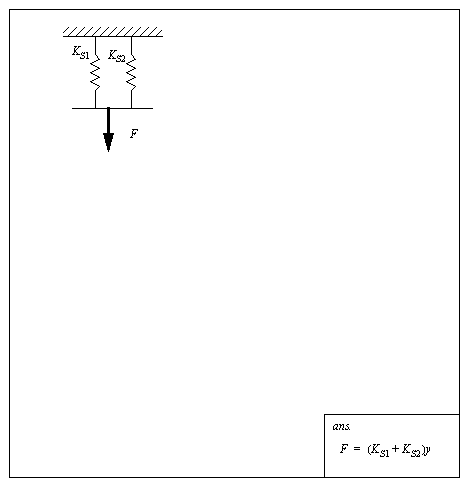
Figure 2.36 Drill problem: Find an equivalent spring for the springs in parallel Consider the drill problem. When an object has no mass, the force applied to one side of the spring will also be applied to the other. The only factor that changes is displacement. 
Figure 2.37 Drill problem: Prove that the force on both sides is equal |