24. CONTINUOUS CONTROL• Feedback control of continuous systems • Control of systems with logical actuators • PID control with continuous actuators • Analysis of PID controlled systems • To understand the concepts behind continuous control • Be able to control a system with logical actuators • Be able to analyze and control system with a PID controller Continuous processes require continuous sensors and/or actuators. For example, an oven temperature can be measured with a thermocouple. Simple decision-based control schemes can use continuous sensor values to control logical outputs, such as a heating element. Linear control equations can be used to examine continuous sensor values and set outputs for continuous actuators, such as a variable position gas valve. 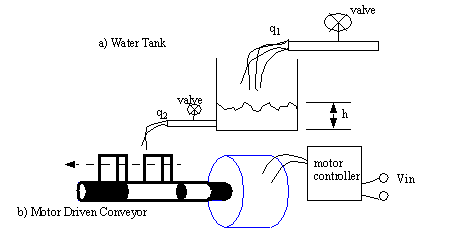
Figure 24.1 Continuous Systems Two continuous control systems are shown in Figure 24.1 Continuous Systems. The water tank can be controlled valves. In a simple control scheme, one of the valves is set by the process, but we control the other to maximize some control object. If the water tank was actually a city water tank, the outlet valve would be the domestic and industrial water users. The inlet valve would be set to keep the tank level at maximum. If the level drops there will be a reduced water pressure at the outlet, and if the tank becomes too full it could overflow. The conveyor will move boxes between stations. Two common choices are to have it move continuously, or to move the boxes between positions, and then stop. When starting and stopping the boxes should be accelerated quickly, but not so quickly that they slip. And, the conveyor should stop at precise positions. In both of these systems, a good control system design will result in better performance. A mechanical control system is pictured in Figure 24.1 A Feedback Controller that could be used for the water tank in Figure 24.1 Continuous Systems. This controller will adjust the valve position, therefore controlling the flow rate into the tank. The height of the fluid in the tank will change the hydrostatic pressure at the bottom of the tank. A pressure line is connected to a pressure cell. As the pressure inside the cell changes, the cell will expand and contract, opening and closing the valve. As the tank fills the pressure becomes higher, the cell expands, and the valve closes, reducing the flow in. The desired height of the tank can be adjusted by sliding the pressure cell up/down a distance x. In this example the height x is called the setpoint. The control variable is the position of the valve, and, the feedback variable is the water pressure from the tank. The controller is the pressure cell. 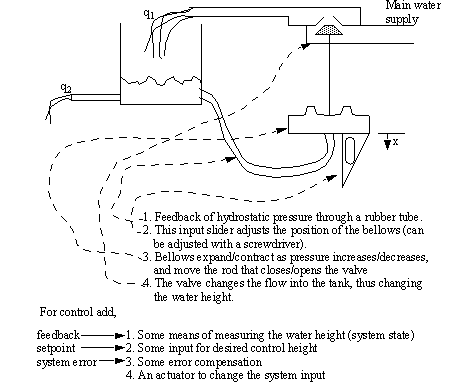
Figure 24.1 A Feedback Controller Continuous control systems typically need a target value, this is called a setpoint. The controller should be designed with some objective in mind. Typical objectives are listed below. fastest response - reach the setpoint as fast as possible (e.g., hard drive speed) smooth response - reduce acceleration and jerks (e.g., elevators) energy efficient - minimize energy usage (e.g., industrial oven) noise immunity - ignores disturbances in the system (e.g., variable wind gusts) An engineer can design a controller mathematically when performance and stability are important issues. A common industrial practice is to purchase a PID unit, connect it to a process, and tune it through trial and error. This is suitable for simpler systems, but these systems are less efficient and prone to instability. In other words it is quick and easy, but these systems can go out-of-control. |