INDUSTRIAL SENSORSThis section describes sensors that will be of use for industrial measurements. The sections have been divided by the phenomena to be measured. Where possible details are provided. 22.1.1 Angular Displacement22.1.1.1 - PotentiometersPotentiometers measure the angular position of a shaft using a variable resistor. A potentiometer is shown in Figure 22.1 A Potentiometer. The potentiometer is resistor, normally made with a thin film of resistive material. A wiper can be moved along the surface of the resistive film. As the wiper moves toward one end there will be a change in resistance proportional to the distance moved. If a voltage is applied across the resistor, the voltage at the wiper interpolate the voltages at the ends of the resistor. 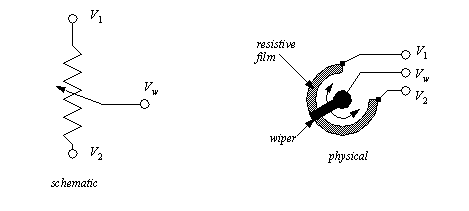
The potentiometer in Figure 22.1 A Potentiometer as a Voltage Divider is being used as a voltage divider. As the wiper rotates the output voltage will be proportional to the angle of rotation. 
Figure 22.1 A Potentiometer as a Voltage Divider Potentiometers are popular because they are inexpensive, and don’t require special signal conditioners. But, they have limited accuracy, normally in the range of 1% and they are subject to mechanical wear. Potentiometers measure absolute position, and they are calibrated by rotating them in their mounting brackets, and then tightening them in place. The range of rotation is normally limited to less than 360 degrees or multiples of 360 degrees. Some potentiometers can rotate without limits, and the wiper will jump from one end of the resistor to the other. Faults in potentiometers can be detected by designing the potentiometer to never reach the ends of the range of motion. If an output voltage from the potentiometer ever reaches either end of the range, then a problem has occurred, and the machine can be shut down. Two examples of problems that might cause this are wires that fall off, or the potentiometer rotates in its mounting. 22.1.2 EncodersEncoders use rotating disks with optical windows, as shown in Figure 22.1 An Encoder Disk. The encoder contains an optical disk with fine windows etched into it. Light from emitters passes through the openings in the disk to detectors. As the encoder shaft is rotated, the light beams are broken. The encoder shown here is a quadrature encode, and it will be discussed later. 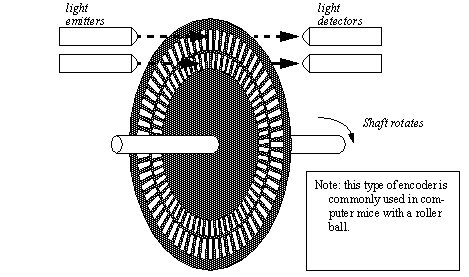
There are two fundamental types of encoders; absolute and incremental. An absolute encoder will measure the position of the shaft for a single rotation. The same shaft angle will always produce the same reading. The output is normally a binary or grey code number. An incremental (or relative) encoder will output two pulses that can be used to determine displacement. Logic circuits or software is used to determine the direction of rotation, and count pulses to determine the displacement. The velocity can be determined by measuring the time between pulses. Encoder disks are shown in Figure 22.1 Encoder Disks. The absolute encoder has two rings, the outer ring is the most significant digit of the encoder, the inner ring is the least significant digit. The relative encoder has two rings, with one ring rotated a few degrees ahead of the other, but otherwise the same. Both rings detect position to a quarter of the disk. To add accuracy to the absolute encoder more rings must be added to the disk, and more emitters and detectors. To add accuracy to the relative encoder we only need to add more windows to the existing two rings. Typical encoders will have from 2 to thousands of windows per ring. 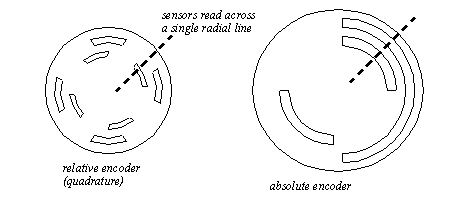
When using absolute encoders, the position during a single rotation is measured directly. If the encoder rotates multiple times then the total number of rotations must be counted separately. When using a relative encoder, the distance of rotation is determined by counting the pulses from one of the rings. If the encoder only rotates in one direction then a simple count of pulses from one ring will determine the total distance. If the encoder can rotate both directions a second ring must be used to determine when to subtract pulses. The quadrature scheme, using two rings, is shown in Figure 22.1 Quadrature Encoders. The signals are set up so that one is out of phase with the other. Notice that for different directions of rotation, input B either leads or lags A. 
Figure 22.1 Quadrature Encoders Interfaces for encoders are commonly available for PLCs and as purchased units. Newer PLCs will also allow two normal inputs to be used to decode encoder inputs. Normally absolute and relative encoders require a calibration phase when a controller is turned on. This normally involves moving an axis until it reaches a logical sensor that marks the end of the range. The end of range is then used as the zero position. Machines using encoders, and other relative sensors, are noticeable in that they normally move to some extreme position before use. 22.1.2.1 - TachometersTachometers measure the velocity of a rotating shaft. A common technique is to mount a magnet to a rotating shaft. When the magnetic moves past a stationary pick-up coil, current is induced. For each rotation of the shaft there is a pulse in the coil, as shown in Figure 22.1 A Magnetic Tachometer. When the time between the pulses is measured the period for one rotation can be found, and the frequency calculated. This technique often requires some signal conditioning circuitry. 
Figure 22.1 A Magnetic Tachometer Another common technique uses a simple permanent magnet DC generator (note: you can also use a small DC motor). The generator is hooked to the rotating shaft. The rotation of a shaft will induce a voltage proportional to the angular velocity. This technique will introduce some drag into the system, and is used where efficiency is not an issue. Both of these techniques are common, and inexpensive. 22.1.3 Linear Position22.1.3.1 - PotentiometersRotational potentiometers were discussed before, but potentiometers are also available in linear/sliding form. These are capable of measuring linear displacement over long distances. Figure 22.1 Linear Potentiometer shows the output voltage when using the potentiometer as a voltage divider. 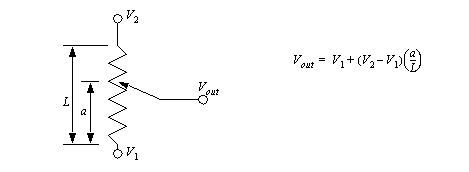
Figure 22.1 Linear Potentiometer Linear/sliding potentiometers have the same general advantages and disadvantages of rotating potentiometers. 22.1.3.2 - Linear Variable Differential Transformers (LVDT)Linear Variable Differential Transformers (LVDTs) measure linear displacements over a limited range. The basic device is shown in Figure 22.1 An LVDT. It consists of outer coils with an inner moving magnetic core. High frequency alternating current (AC) is applied to the center coil. This generates a magnetic field that induces a current in the two outside coils. The core will pull the magnetic field towards it, so in the figure more current will be induced in the left hand coil. The outside coils are wound in opposite directions so that when the core is in the center the induced currents cancel, and the signal out is zero (0Vac). The magnitude of the signal out voltage on either line indicates the position of the core. Near the center of motion the change in voltage is proportional to the displacement. But, further from the center the relationship becomes nonlinear. 

Figure 22.1 A Simple Signal Conditioner for an LVDT These devices are more accurate than linear potentiometers, and have less friction. Typical applications for these devices include measuring dimensions on parts for quality control. They are often used for pressure measurements with Bourdon tubes and bellows/diaphragms. A major disadvantage of these sensors is the high cost, often in the thousands. 22.1.3.3 - Moire FringesHigh precision linear displacement measurements can be made with Moire Fringes, as shown in Figure 22.1 The Moire Fringe Effect. Both of the strips are transparent (or reflective), with black lines at measured intervals. The spacing of the lines determines the accuracy of the position measurements. The stationary strip is offset at an angle so that the strips interfere to give irregular patterns. As the moving strip travels by a stationary strip the patterns will move up, or down, depending upon the speed and direction of motion. 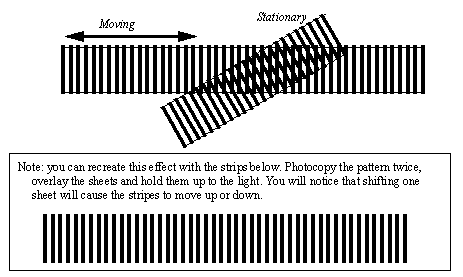
Figure 22.1 The Moire Fringe Effect A device to measure the motion of the moire fringes is shown in Figure 22.1 Measuring Motion with Moire Fringes. A light source is collimated by passing it through a narrow slit to make it one slit width. This is then passed through the fringes to be detected by light sensors. At least two light sensors are needed to detect the bright and dark locations. Two sensors, close enough, can act as a quadrature pair, and the same method used for quadrature encoders can be used to determine direction and distance of motion. 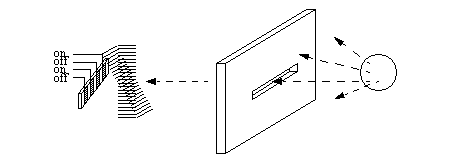
Figure 22.1 Measuring Motion with Moire Fringes These are used in high precision applications over long distances, often meters. They can be purchased from a number of suppliers, but the cost will be high. Typical applications include Coordinate Measuring Machines (CMMs). 22.1.3.4 - AccelerometersAccelerometers measure acceleration using a mass suspended on a force sensor, as shown in Figure 22.1 A Cross Section of an Accelerometer. When the sensor accelerates, the inertial resistance of the mass will cause the force sensor to deflect. By measuring the deflection the acceleration can be determined. In this case the mass is cantilevered on the force sensor. A base and housing enclose the sensor. A small mounting stud (a threaded shaft) is used to mount the accelerometer. 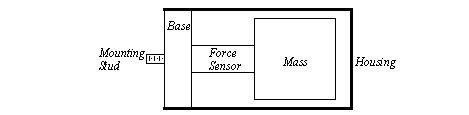
Figure 22.1 A Cross Section of an Accelerometer Accelerometers are dynamic sensors, typically used for measuring vibrations between 10Hz to 10KHz. Temperature variations will affect the accuracy of the sensors. Standard accelerometers can be linear up to 100,000 m/s**2: high shock designs can be used up to 1,000,000 m/s**2. There is often a trade-off between a wide frequency range and device sensitivity (note: higher sensitivity requires a larger mass). Figure 22.1 Piezoelectric Accelerometer Sensitivities shows the sensitivity of two accelerometers with different resonant frequencies. A smaller resonant frequency limits the maximum frequency for the reading. The smaller frequency results in a smaller sensitivity. The units for sensitivity is charge per m/s**2. 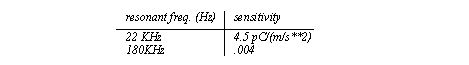
Figure 22.1 Piezoelectric Accelerometer Sensitivities The force sensor is often a small piece of piezoelectric material (discussed later in this chapter). The piezoelectic material can be used to measure the force in shear or compression. Piezoelectric based accelerometers typically have parameters such as, operate well below one forth of the natural frequency The accelerometer is mounted on the vibration source as shown in Figure 22.1 Mounting an Accelerometer. The accelerometer is electrically isolated from the vibration source so that the sensor may be grounded at the amplifier (to reduce electrical noise). Cables are fixed to the surface of the vibration source, close to the accelerometer, and are fixed to the surface as often as possible to prevent noise from the cable striking the surface. Background vibrations can be detected by attaching control electrodes to non-vibrating surfaces. Each accelerometer is different, but some general application guidelines are; • The control vibrations should be less than 1/3 of the signal for the error to be less than 12%). • Mass of the accelerometers should be less than a tenth of the measurement mass. • These devices can be calibrated with shakers, for example a 1g shaker will hit a peak velocity of 9.81 m/s**2. 
Figure 22.1 Mounting an Accelerometer Equipment normally used when doing vibration testing is shown in Figure 22.1 Typical Connection for Accelerometers. The sensor needs to be mounted on the equipment to be tested. A pre-amplifier normally converts the charge generated by the accelerometer to a voltage. The voltage can then be analyzed to determine the vibration frequencies. 
Figure 22.1 Typical Connection for Accelerometers Accelerometers are commonly used for control systems that adjust speeds to reduce vibration and noise. Computer Controlled Milling machines now use these sensors to actively eliminate chatter, and detect tool failure. The signal from accelerometers can be integrated to find velocity and acceleration. Currently accelerometers cost hundreds or thousands per channel. But, advances in micromachining are already beginning to provide integrated circuit accelerometers at a low cost. Their current use is for airbag deployment systems in automobiles. 22.1.4 Forces and Moments22.1.4.1 - Strain GagesStrain gages measure strain in materials using the change in resistance of a wire. The wire is glued to the surface of a part, so that it undergoes the same strain as the part (at the mount point). Figure 22.1 The Electrical Properties of a Wire shows the basic properties of the undeformed wire. Basically, the resistance of the wire is a function of the resistivity, length, and cross sectional area. 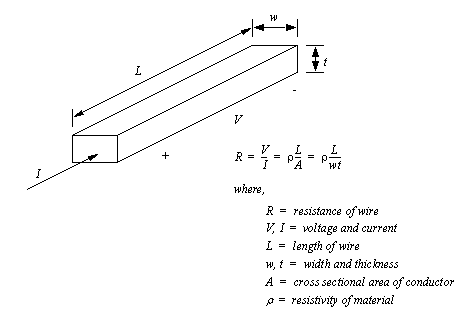
Figure 22.1 The Electrical Properties of a Wire After the wire in Figure 22.1 The Electrical Properties of a Wire has been deformed it will take on the new dimensions and resistance shown in Figure 22.1 The Electrical and Mechanical Properties of the Deformed Wire. If a force is applied as shown, the wire will become longer, as predicted by Young’s modulus. But, the cross sectional area will decrease, as predicted by Poison’s ratio. The new length and cross sectional area can then be used to find a new resistance. 
Figure 22.1 The Electrical and Mechanical Properties of the Deformed Wire 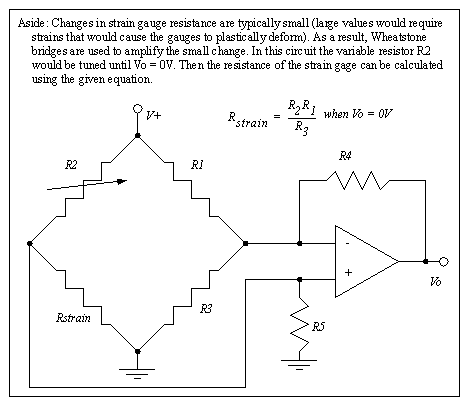
Figure 22.1 Measuring Strain with a Wheatstone Bridge A strain gage must be small for accurate readings, so the wire is actually wound in a uniaxial or rosette pattern, as shown in Figure 22.1 Wire Arrangements in Strain Gages. When using uniaxial gages the direction is important, it must be placed in the direction of the normal stress. (Note: the gages cannot read shear stress.) Rosette gages are less sensitive to direction, and if a shear force is present the gage will measure the resulting normal force at 45 degrees. These gauges are sold on thin films that are glued to the surface of a part. The process of mounting strain gages involves surface cleaning. application of adhesives, and soldering leads to the strain gages. 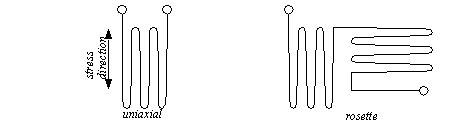
Figure 22.1 Wire Arrangements in Strain Gages A design techniques using strain gages is to design a part with a narrowed neck to mount the strain gage on, as shown in Figure 22.1 Using a Narrow to Increase Strain. In the narrow neck the strain is proportional to the load on the member, so it may be used to measure force. These parts are often called load cells. 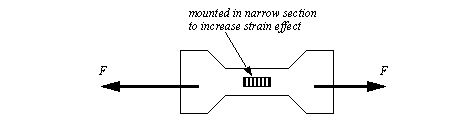
Figure 22.1 Using a Narrow to Increase Strain Strain gauges are inexpensive, and can be used to measure a wide range of stresses with accuracies under 1%. Gages require calibration before each use. This often involves making a reading with no load, or a known load applied. An example application includes using strain gages to measure die forces during stamping to estimate when maintenance is needed. 22.1.4.2 - PiezoelectricWhen a crystal undergoes strain it displaces a small amount of charge. In other words, when the distance between atoms in the crystal lattice changes some electrons are forced out or drawn in. This also changes the capacitance of the crystal. This is known as the Piezoelectric effect. Figure 22.1 The Piezoelectric Effect shows the relationships for a crystal undergoing a linear deformation. The charge generated is a function of the force applied, the strain in the material, and a constant specific to the material. The change in capacitance is proportional to the change in the thickness. 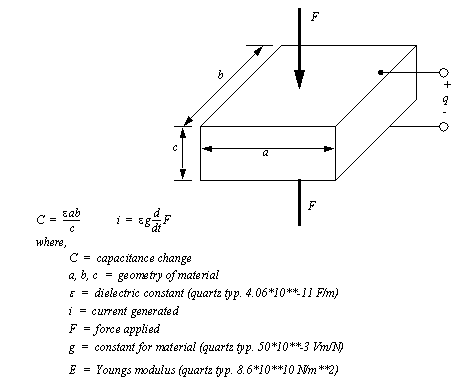
Figure 22.1 The Piezoelectric Effect These crystals are used for force sensors, but they are also used for applications such as microphones and pressure sensors. Applying an electrical charge can induce strain, allowing them to be used as actuators, such as audio speakers. When using piezoelectric sensors charge amplifiers are needed to convert the small amount of charge to a larger voltage. These sensors are best suited to dynamic measurements, when used for static measurements they tend to drift or slowly lose charge, and the signal value will change. 22.1.5 Liquids and GasesThere are a number of factors to be considered when examining liquids and gasses. There are a number of differences factors to be considered when dealing with fluids and gases. Normally a fluid is considered incompressible, while a gas normally follows the ideal gas law. Also, given sufficiently high enough temperatures, or low enough pressures a fluid can be come a gas. 
When flowing, the flow may be smooth, or laminar. In case of high flow rates or unrestricted flow, turbulence may result. The Reynold’s number is used to determine the transition to turbulence. The equation below is for calculation the Reynold’s number for fluid flow in a pipe. A value below 2000 will result in laminar flow. At a value of about 3000 the fluid flow will become uneven. At a value between 7000 and 8000 the flow will become turbulent. 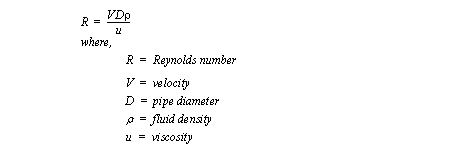
22.1.5.1 - PressureFigure 22.1 Pressure Transducers shows different two mechanisms for pressure measurement. The Bourdon tube uses a circular pressure tube. When the pressure inside is higher than the surrounding air pressure (14.7psi approx.) the tube will straighten. A position sensor, connected to the end of the tube, will be elongated when the pressure increases. 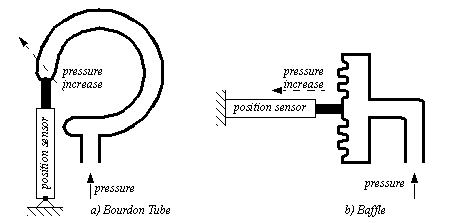
Figure 22.1 Pressure Transducers These sensors are very common and have typical accuracies of 0.5%. 22.1.5.2 - Venturi ValvesWhen a flowing fluid or gas passes through a narrow pipe section (neck) the pressure drops. If there is no flow the pressure before and after the neck will be the same. The faster the fluid flow, the greater the pressure difference before and after the neck. This is known as a Venturi valve. Figure 22.1 A Venturi Valve shows a Venturi valve being used to measure a fluid flow rate. The fluid flow rate will be proportional to the pressure difference before and at the neck (or after the neck) of the valve. 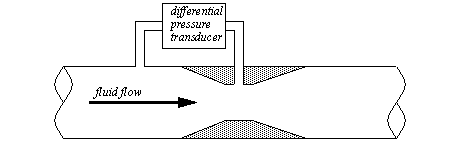

Figure 22.1 The Pressure Relationship for a Venturi Valve Venturi valves allow pressures to be read without moving parts, which makes them very reliable and durable. They work well for both fluids and gases. It is also common to use Venturi valves to generate vacuums for actuators, such as suction cups. 22.1.5.3 - Coriolis Flow MeterFluid passes through thin tubes, causing them to vibrate. As the fluid approaches the point of maximum vibration it accelerates. When leaving the point it decelerates. The result is a distributed force that causes a bending moment, and hence twisting of the pipe. The amount of bending is proportional to the velocity of the fluid flow. These devices typically have a large constriction on the flow, and result is significant loses. Some of the devices also use bent tubes to increase the sensitivity, but this also increases the flow resistance. The typical accuracy for a Coriolis flowmeter is 0.1%. 22.1.5.4 - Magnetic Flow MeterA magnetic sensor applies a magnetic field perpendicular to the flow of a conductive fluid. As the fluid moves, the electrons in the fluid experience an electromotive force. The result is that a potential (voltage) can be measured perpendicular to the direction of the flow and the magnetic field. The higher the flow rate, the greater the voltage. The typical accuracy for these sensors is 0.5%. These flowmeters don’t oppose fluid flow, and so they don’t result in pressure drops. 22.1.5.5 - Ultrasonic Flow MeterA transmitter emits a high frequency sound at point on a tube. The signal must then pass through the fluid to a detector where it is picked up. If the fluid is flowing in the same direction as the sound it will arrive sooner. If the sound is against the flow it will take longer to arrive. In a transit time flow meter two sounds are used, one traveling forward, and the other in the opposite direction. The difference in travel time for the sounds is used to determine the flow velocity. A doppler flowmeter bounces a soundwave off particle in a flow. If the particle is moving away from the emitter and detector pair, then the detected frequency will be lowered, if it is moving towards them the frequency will be higher. The transmitter and receiver have a minimal impact on the fluid flow, and therefore don’t result in pressure drops. 22.1.5.6 - Vortex Flow MeterFluid flowing past a large (typically flat) obstacle will shed vortices. The frequency of the vortices will be proportional to the flow rate. Measuring the frequency allows an estimate of the flow rate. These sensors tend be low cost and are popular for low accuracy applications. 22.1.5.7 - Positive Displacement MetersIn some cases more precise readings of flow rates and volumes may be required. These can be obtained by using a positive displacement meter. In effect these meters are like pumps run in reverse. As the fluid is pushed through the meter it produces a measurable output, normally on a rotating shaft. 22.1.5.8 - Pitot TubesGas flow rates can be measured using Pitot tubes, as shown in Figure 22.1 Pitot Tubes for Measuring Gas Flow Rates. These are small tubes that project into a flow. The diameter of the tube is small (typically less than 1/8") so that it doesn’t affect the flow. 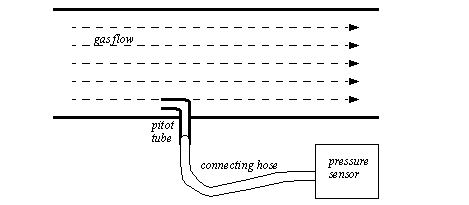
Figure 22.1 Pitot Tubes for Measuring Gas Flow Rates 22.1.6 TemperatureTemperature measurements are very common with control systems. The temperature ranges are normally described with the following classifications. very low temperatures <-60 deg C - e.g. superconductors in MRI units low temperature measurement -60 to 0 deg C - e.g. freezer controls fine temperature measurements 0 to 100 deg C - e.g. environmental controls high temperature measurements <3000 deg F - e.g. metal refining/processing 22.1.6.1 - Resistive Temperature Detectors (RTDs)When a metal wire is heated the resistance increases. So, a temperature can be measured using the resistance of a wire. Resistive Temperature Detectors (RTDs) normally use a wire or film of platinum, nickel, copper or nickel-iron alloys. The metals are wound or wrapped over an insulator, and covered for protection. The resistances of these alloys are shown in Figure 22.1 RTD Properties. 
These devices have positive temperature coefficients that cause resistance to increase linearly with temperature. A platinum RTD might have a resistance of 100 ohms at 0C, that will increase by 0.4 ohms/°C. The total resistance of an RTD might double over the temperature range. A current must be passed through the RTD to measure the resistance. (Note: a voltage divider can be used to convert the resistance to a voltage.) The current through the RTD should be kept to a minimum to prevent self heating. These devices are more linear than thermocouples, and can have accuracies of 0.05%. But, they can be expensive 22.1.6.2 - ThermocouplesEach metal has a natural potential level, and when two different metals touch there is a small potential difference, a voltage. (Note: when designing assemblies, dissimilar metals should not touch, this will lead to corrosion.) Thermocouples use a junction of dissimilar metals to generate a voltage proportional to temperature. This principle was discovered by T.J. Seebeck. The basic calculations for thermocouples are shown in Figure 22.1 Thermocouple Calculations. This calculation provides the measured voltage using a reference temperature and a constant specific to the device. The equation can also be rearranged to provide a temperature given a voltage. 
Figure 22.1 Thermocouple Calculations The list in Table 1 shows different junction types, and the normal temperature ranges. Both thermocouples, and signal conditioners are commonly available, and relatively inexpensive. For example, most PLC vendors sell thermocouple input cards that will allow multiple inputs into the PLC. 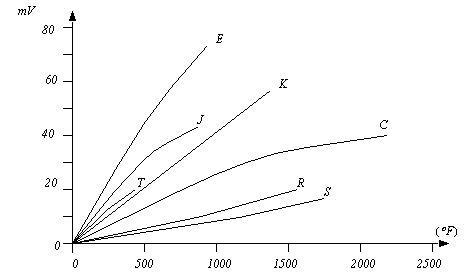
Figure 22.1 Thermocouple Temperature Voltage Relationships (Approximate) The junction where the thermocouple is connected to the measurement instrument is normally cooled to reduce the thermocouple effects at those junctions. When using a thermocouple for precision measurement, a second thermocouple can be kept at a known temperature for reference. A series of thermocouples connected together in series produces a higher voltage and is called a thermopile. Readings can approach an accuracy of 0.5%. 22.1.6.3 - ThermistorsThermistors are non-linear devices, their resistance will decrease with an increase in temperature. (Note: this is because the extra heat reduces electron mobility in the semiconductor.) The resistance can change by more than 1000 times. The basic calculation is shown in Figure 22.1 Thermistor Calculations. often metal oxide semiconductors The calculation uses a reference temperature and resistance, with a constant for the device, to predict the resistance at another temperature. The expression can be rearranged to calculate the temperature given the resistance. 
Figure 22.1 Thermistor Calculations 
Figure 22.1 Thermistor Signal Conditioning Circuit Thermistors are small, inexpensive devices that are often made as beads, or metallized surfaces. The devices respond quickly to temperature changes, and they have a higher resistance, so junction effects are not an issue. Typical accuracies are 1%, but the devices are not linear, have a limited temperature/resistance range and can be self heating. 22.1.6.4 - Other SensorsIC sensors are becoming more popular. They output a digital reading and can have accuracies better than 0.01%. But, they have limited temperature ranges, and require some knowledge of interfacing methods for serial or parallel data. Pyrometers are non-contact temperature measuring devices that use radiated heat. These are normally used for high temperature applications, or for production lines where it is not possible to mount other sensors to the material. 22.1.7 Light22.1.7.1 - Light Dependant Resistors (LDR)Light dependant resistors (LDRs) change from high resistance (>Mohms) in bright light to low resistance (<Kohms) in the dark. The change in resistance is non-linear, and is also relatively slow (ms). 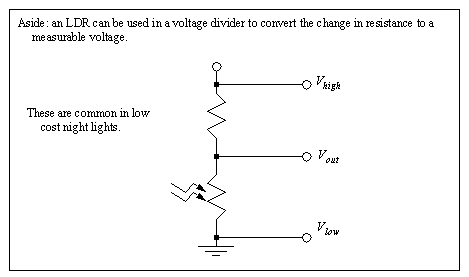
Figure 22.1 A Light Level Detector Circuit 22.1.8 Chemical22.1.8.1 - pHThe pH of an ionic fluid can be measured over the range from a strong base (alkaline) with pH=14, to a neutral value, pH=7, to a strong acid, pH=0. These measurements are normally made with electrodes that are in direct contact with the fluids. 22.1.8.2 - ConductivityConductivity of a material, often a liquid is often used to detect impurities. This can be measured directly be applying a voltage across two plates submerged in the liquid and measuring the current. High frequency inductive fields is another alternative. 22.1.9 OthersA number of other detectors/sensors are listed below, Combustion - gases such as CO2 can be an indicator of combustion |