When developing a complex system it is desirable to create additional function blocks. This can be done with other FBDs, or using other IEC 61131-3 program types. Figure 20.1 Function Block Equivalencies shows a divide function block created using ST. In this example the first statement declares it as a FUNCTION_BLOCK called divide. The input variables a and b, and the output variable c are declared. In the function the denominator is checked to make sure it is not 0. If not, the division will be performed, otherwise the output will be zero.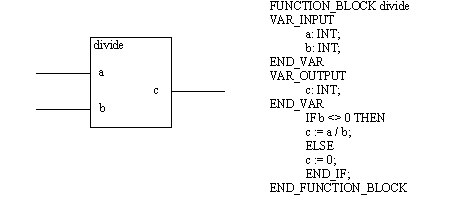