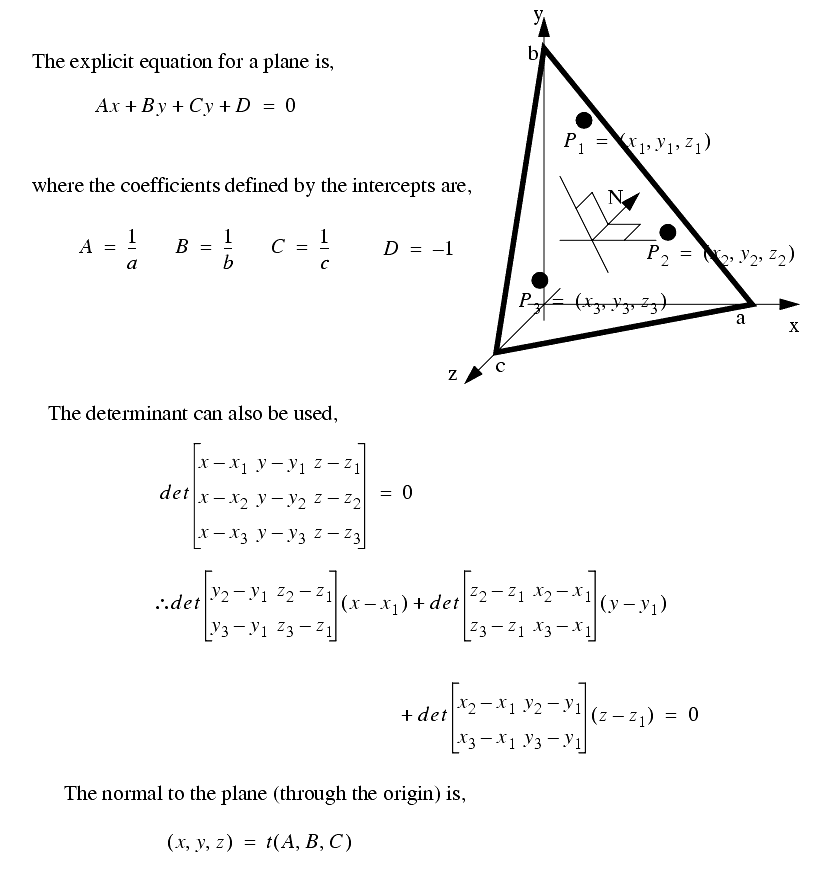2.3 SPATIAL RELATIONSHIPS

---

2.3.1 Trigonometry

The basic trigonometry functions are,

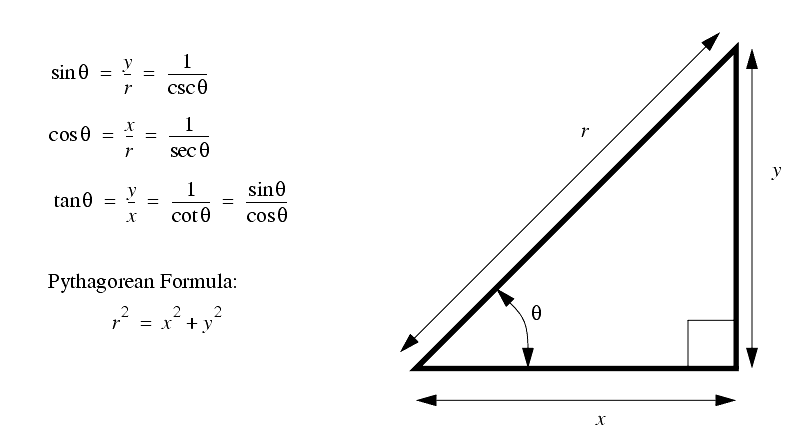
Graphs of these functions are given below,

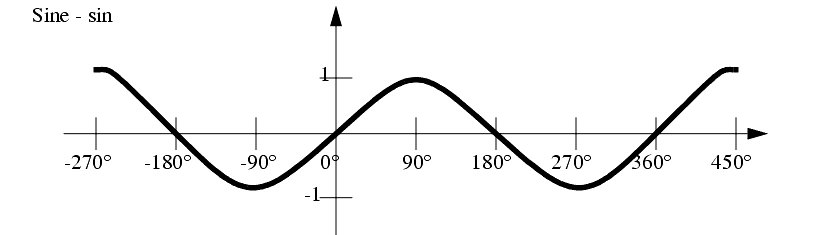
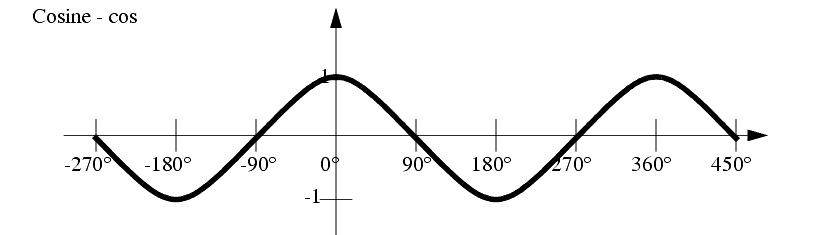
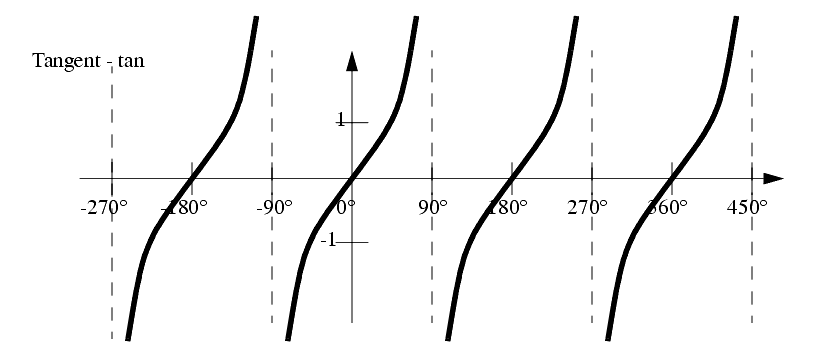
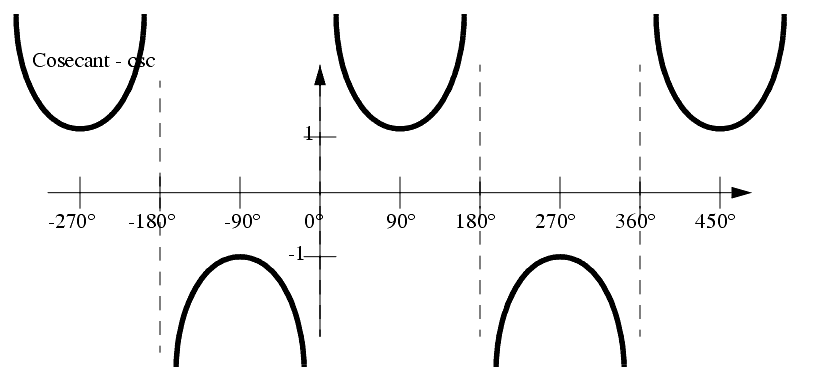
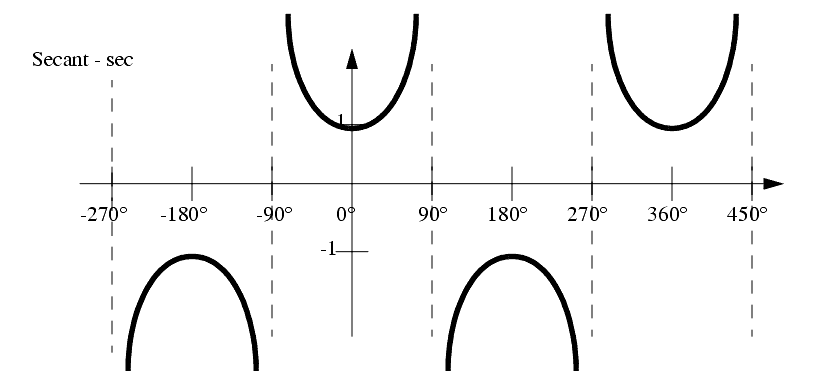
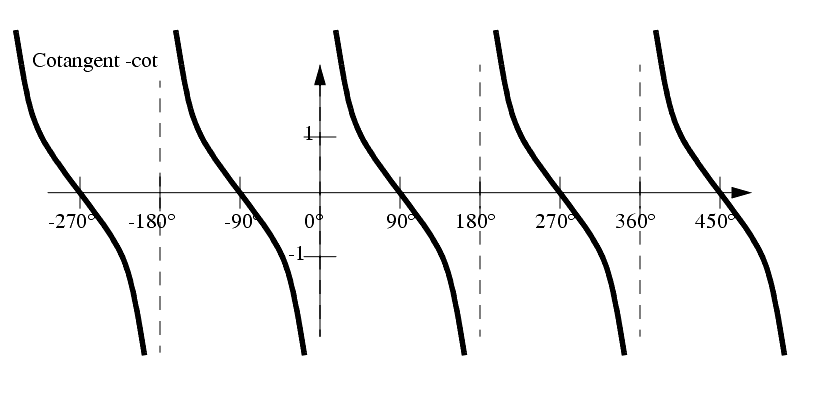
NOTE: Keep in mind when finding these trig values, that any value that does not lie in the right hand quadrants of cartesian space, may need additions of ±90° or ±180°.

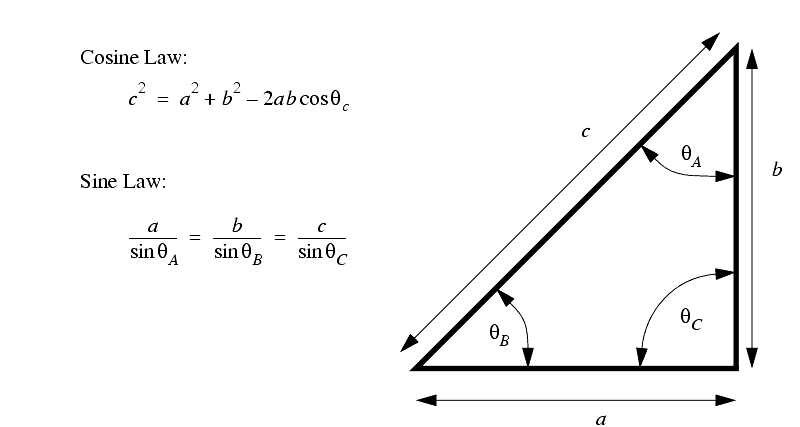
Now a group of trigonometric relationships will be given. These are often best used when attempting to manipulate equations.

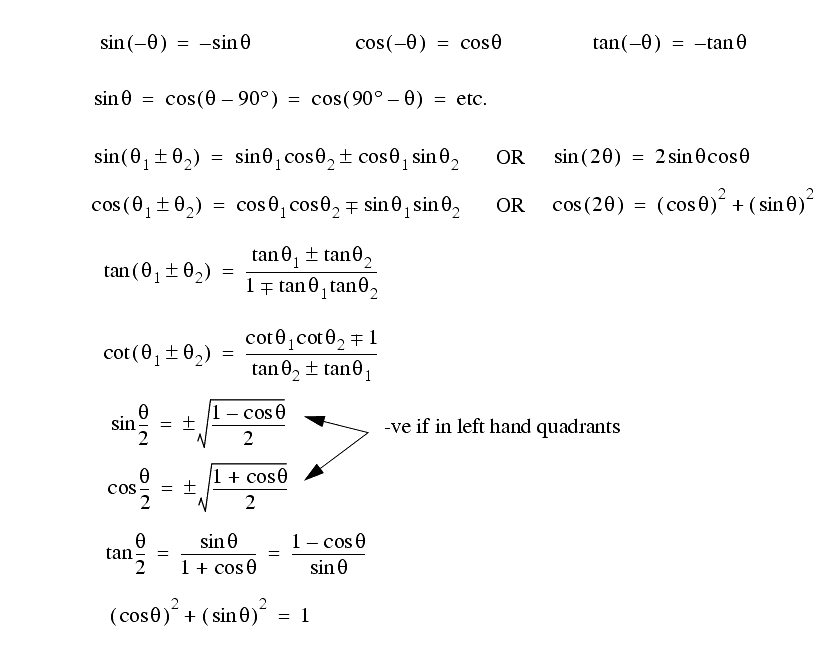
These can also be related to complex exponents,

2.3.2 Hyperbolic Functions

The basic definitions are given below,

some of the basic relationships are,

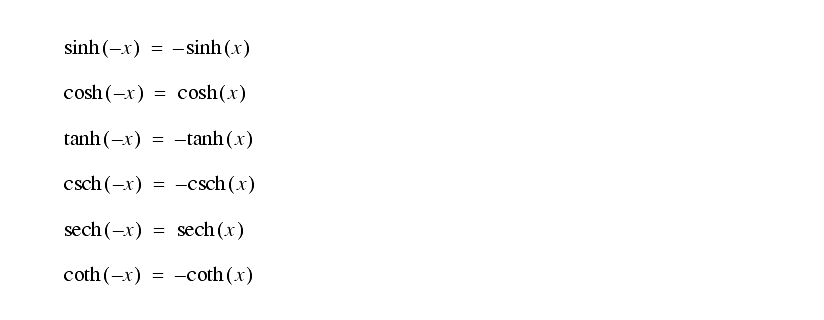
Some of the more advanced relationships are,

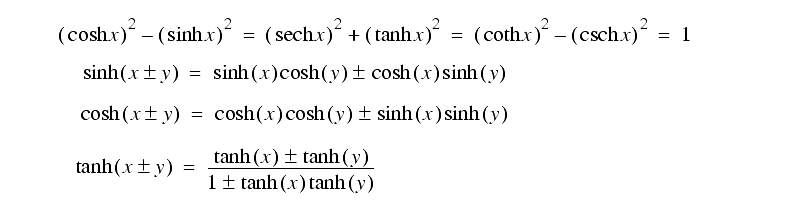
Some of the relationships between the hyperbolic, and normal trigonometry functions are,

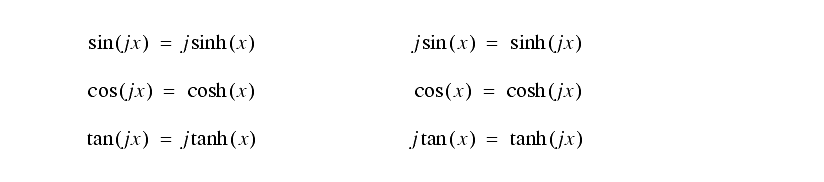
2.3.2.1 - Practice Problems

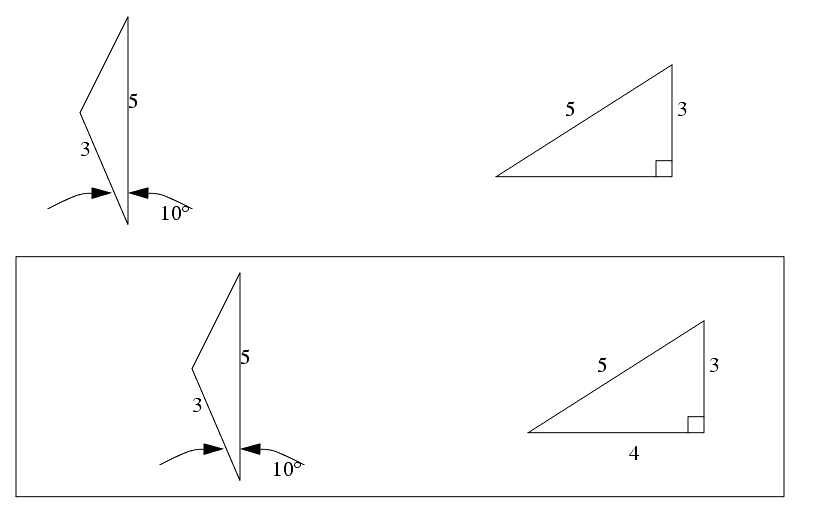
3. Find all of the missing side lengths and corner angles on the two triangles below,

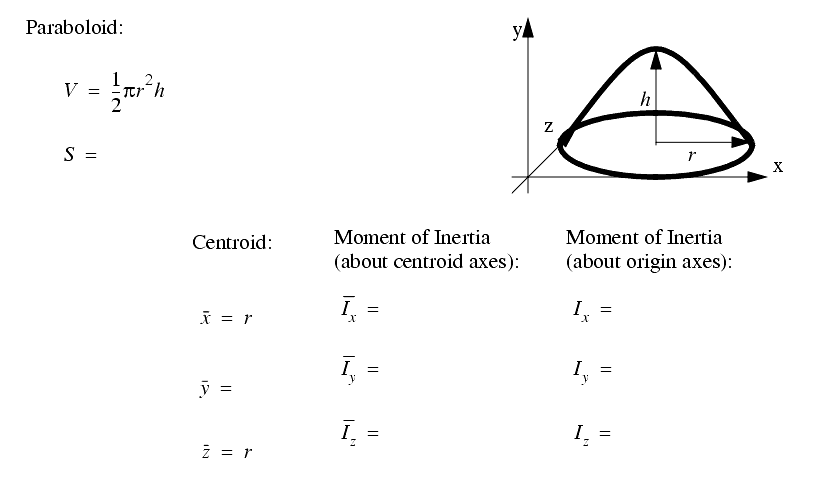
2.3.3 Geometry

****************** ADD IN MASS MOMENTS AND DESCRIPTIONS ************

A set of the basic 2D and 3D geometric primitives are given, and the notation used is described below,

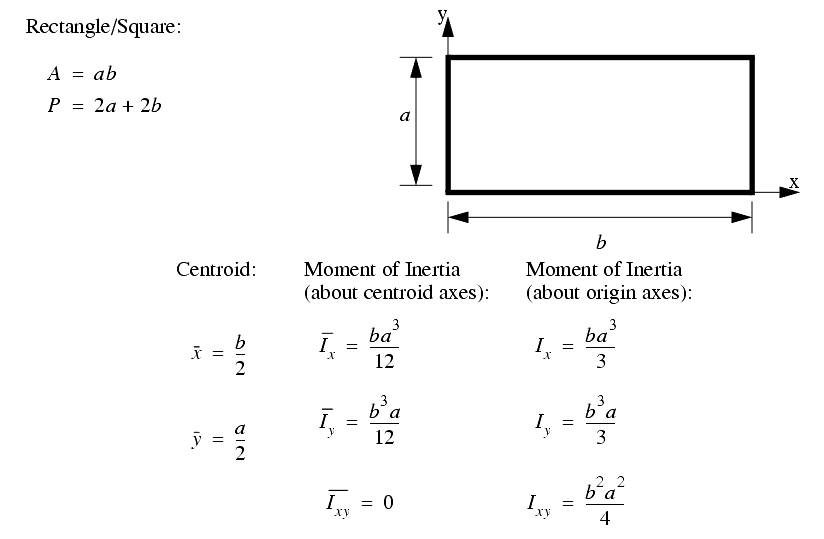
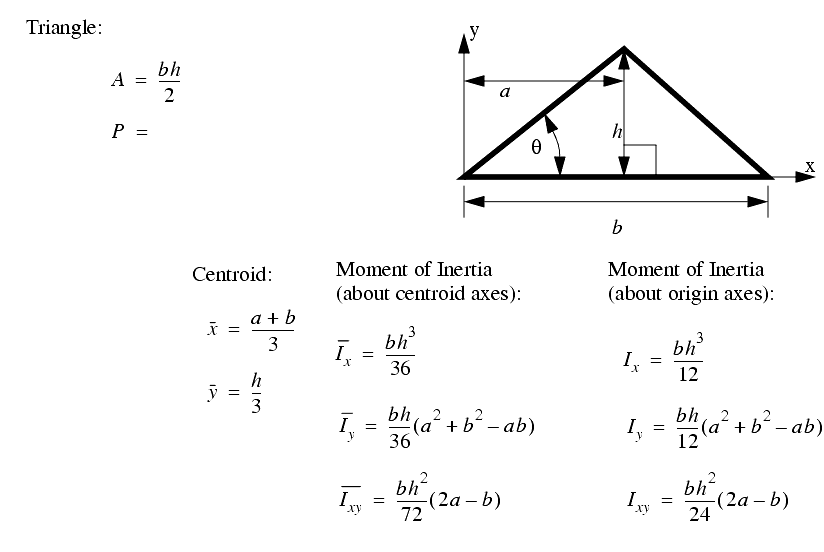
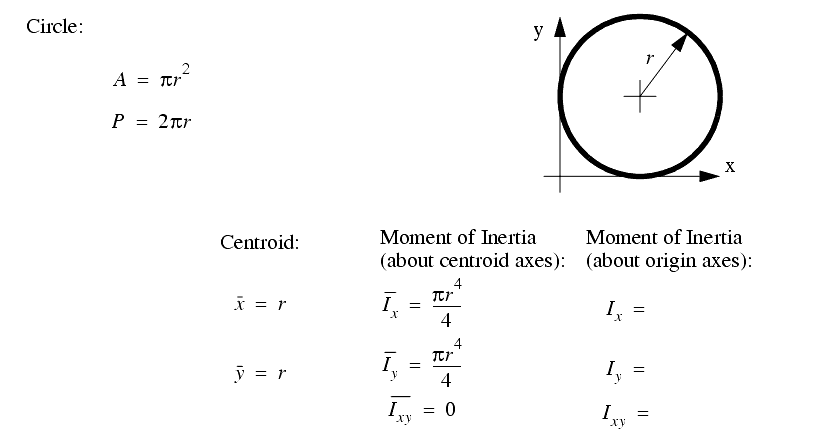
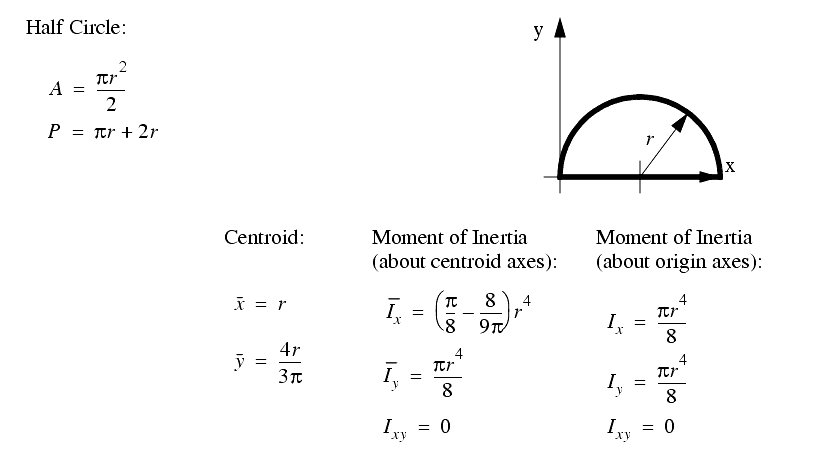
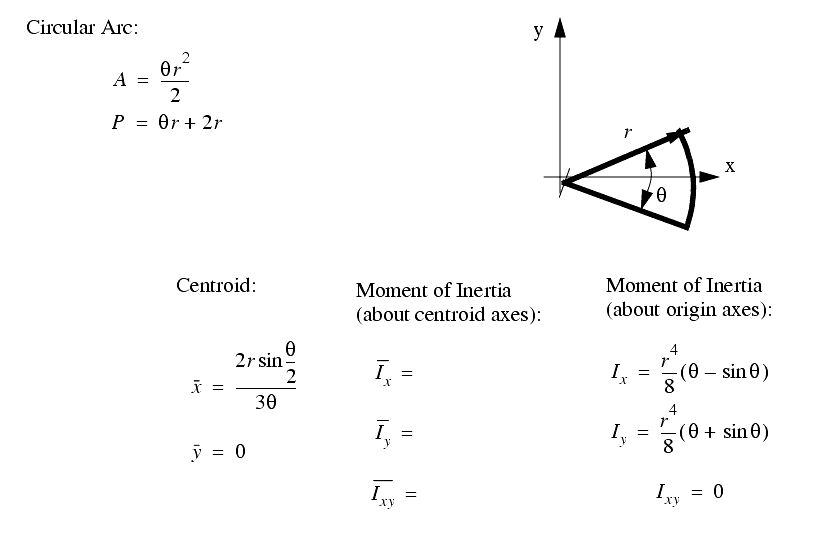
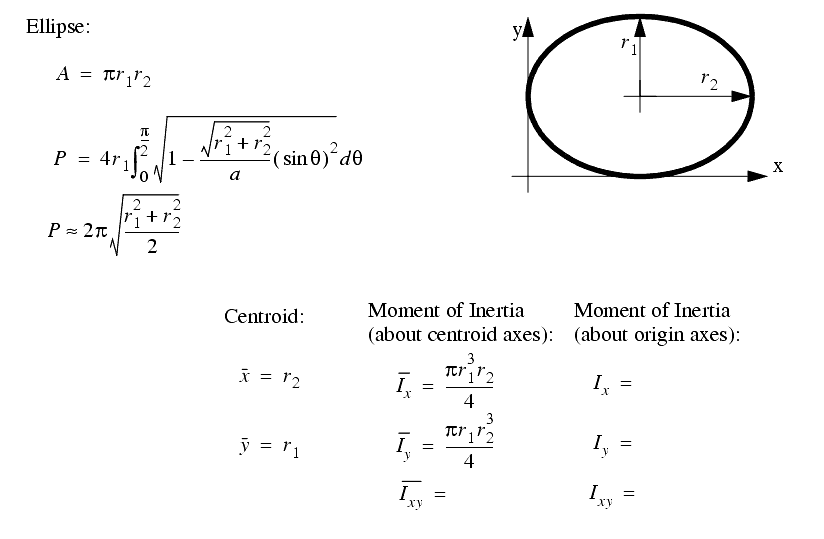
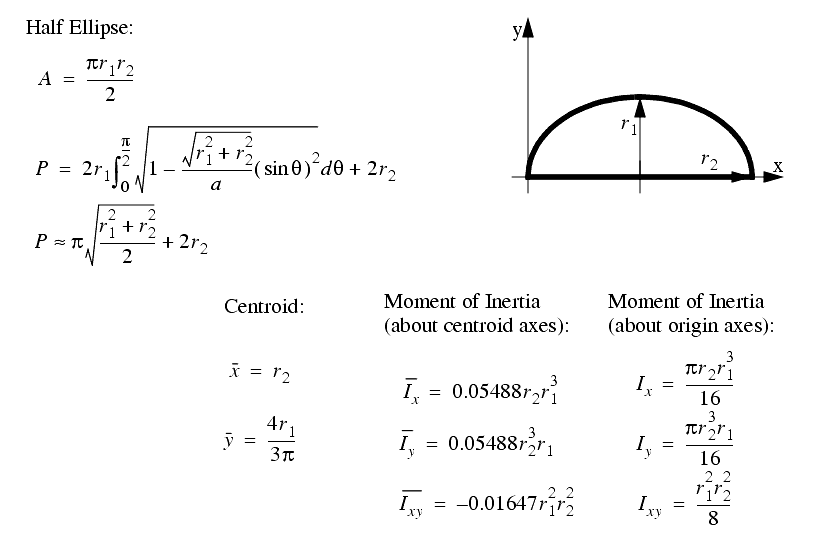
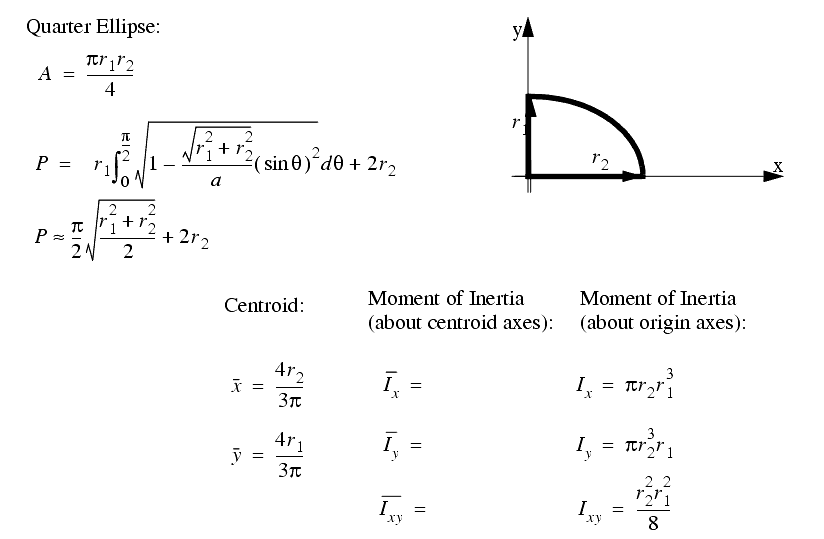
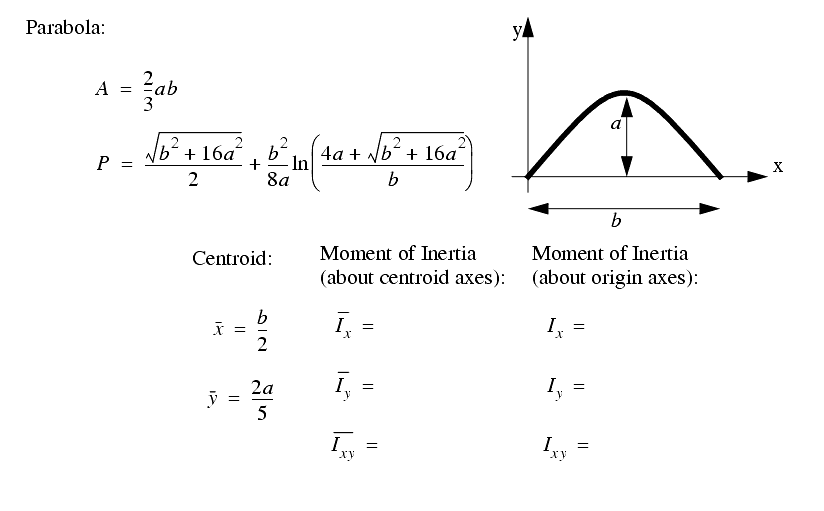
A general class of geometries are conics. This for is shown below, and can be used to represent many of the simple shapes represented by a polynomial.

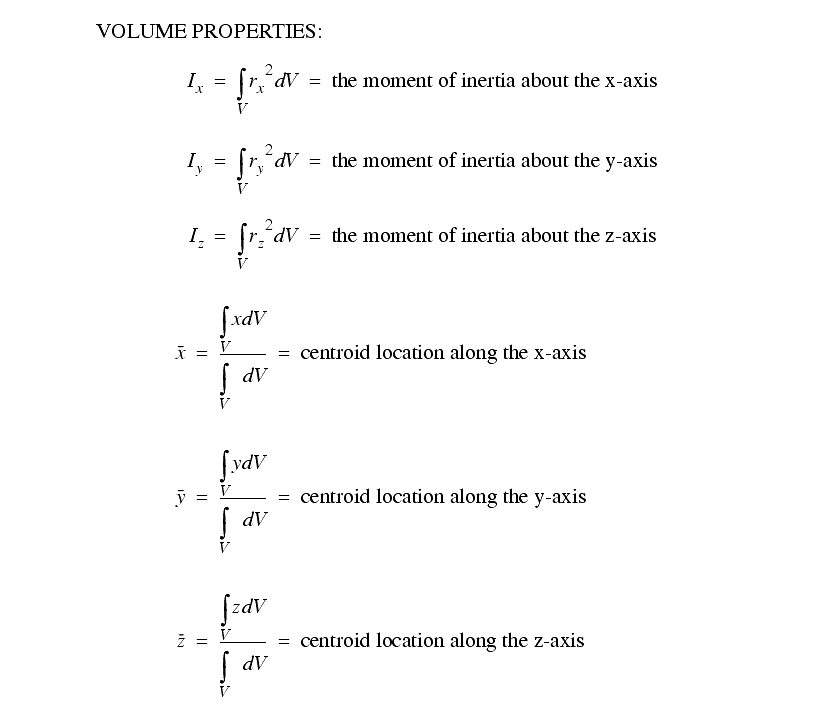
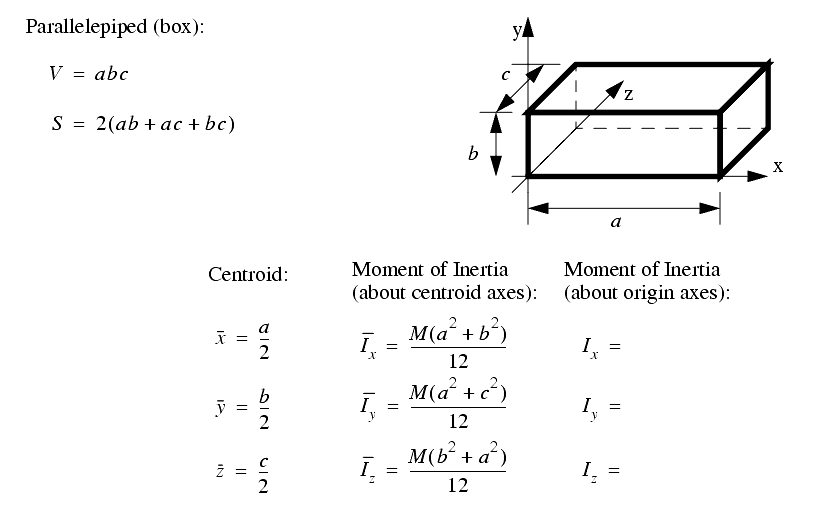
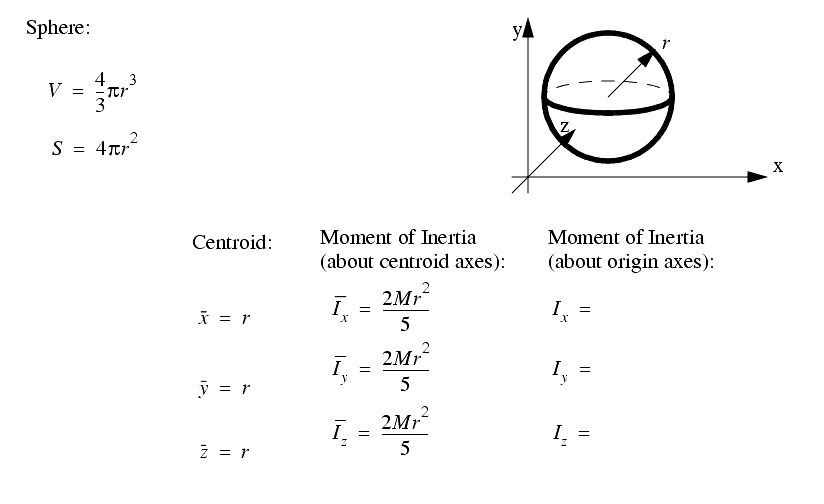
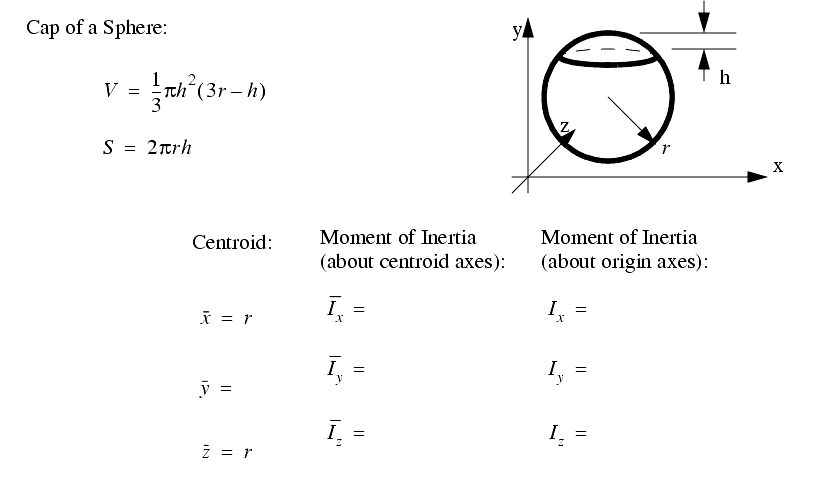
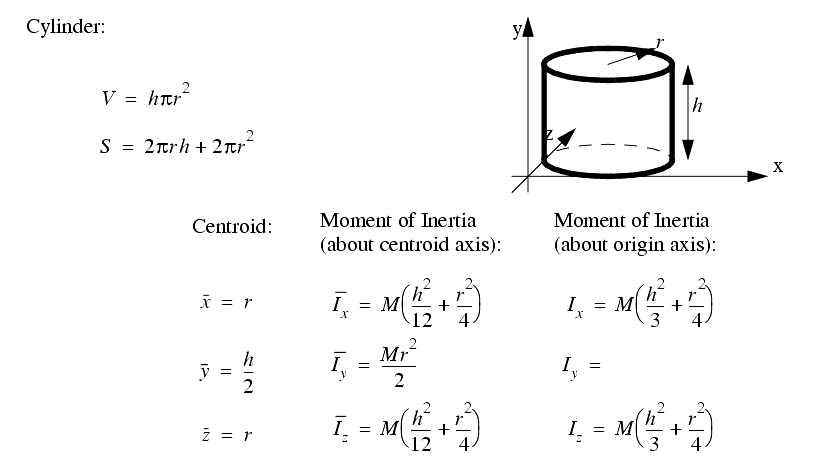
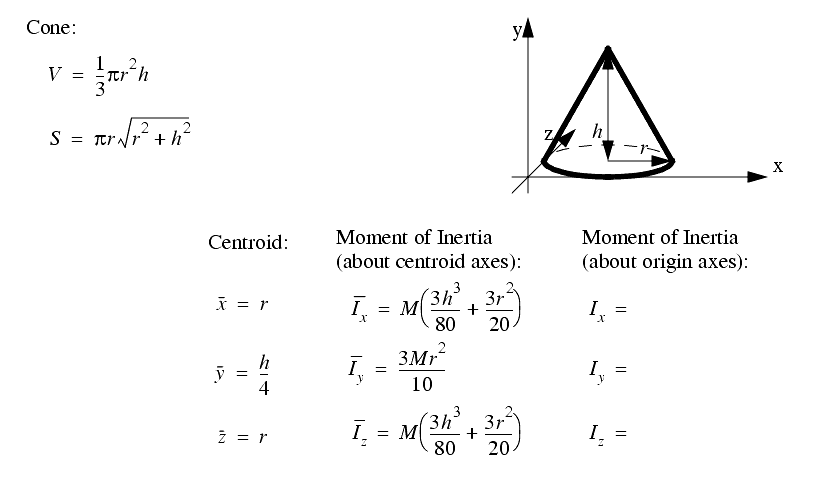
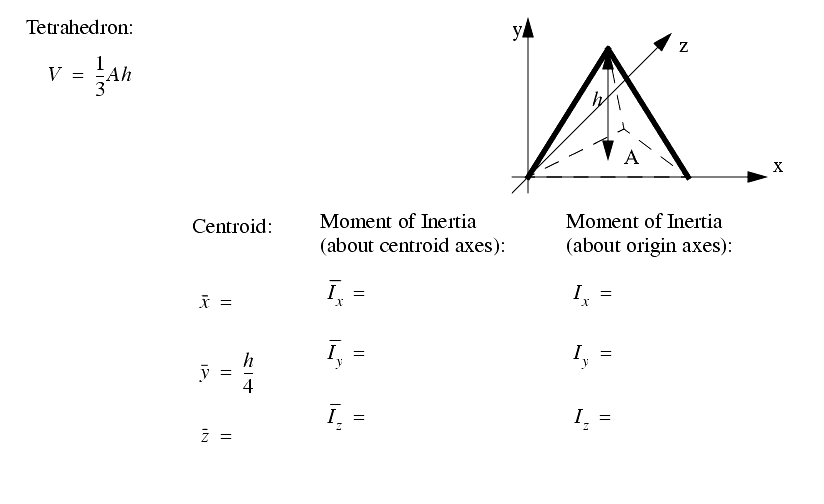
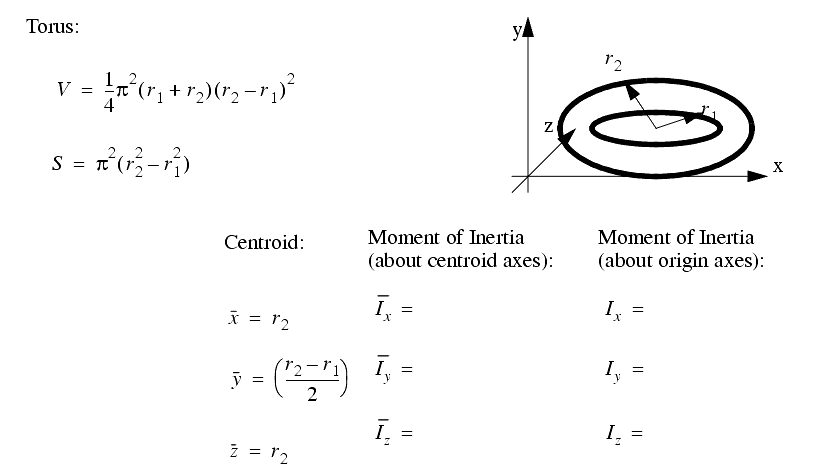
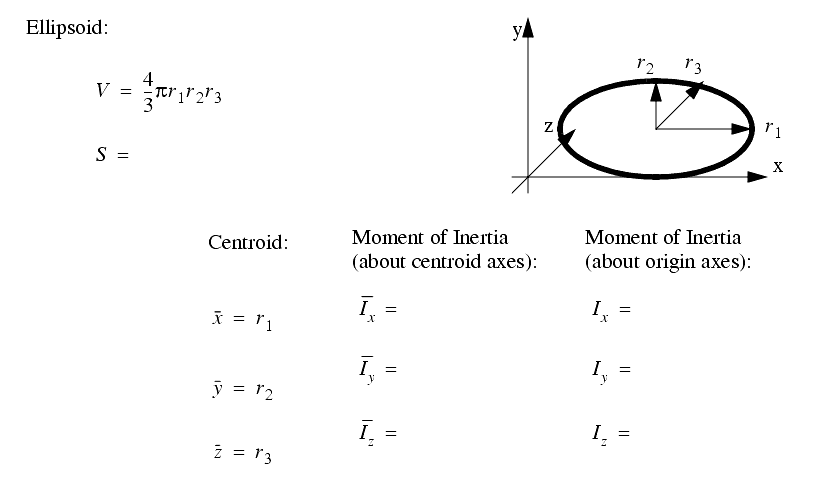
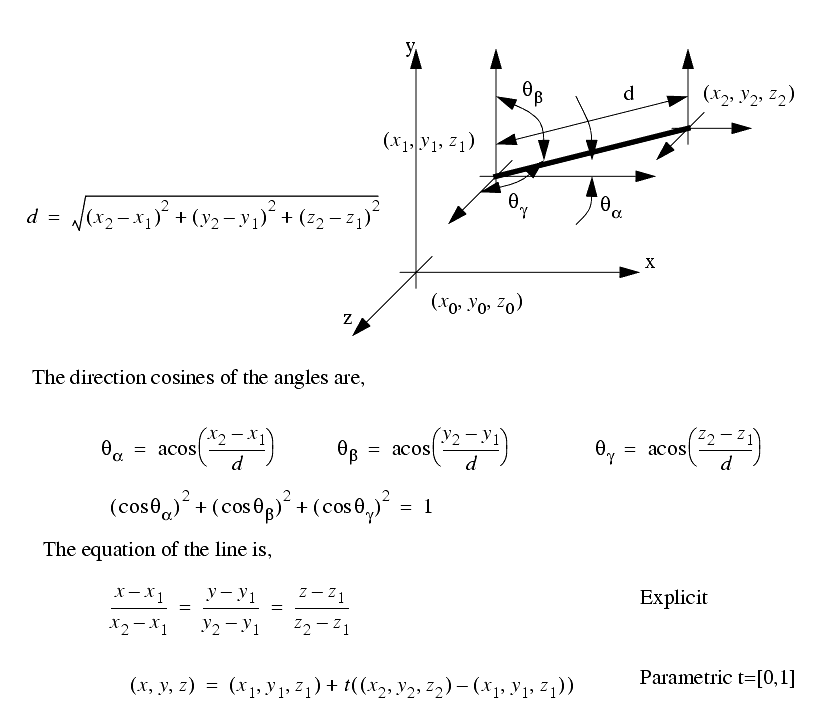
2.3.4 Planes, Lines, etc.

The most fundamental mathematical geometry is a line. The basic relationships are given below,

If we assume a line is between two points in space, and that at one end we have a local reference frame, there are some basic relationships that can be derived.

The relationships for a plane are,