17.1 SAMPLES AS IMPULSE FUNCTION

---

An impulse function is a very (infinitely) thin but has a weight of 1. We can approximate this function with a finite width pulse. In both figures the delta function has been shifted in time.

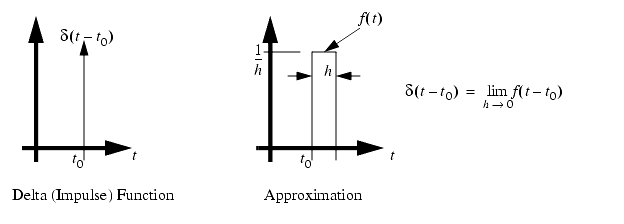
Some of these basic properties are,

Now consider a train of sample pulses with a regular interval T,

The form derived above will allow a z-transform later.

We can also recognize that if a function X(t) has a period less than the sample period `T' then X*(t) will not be a reasonable sample of X(t). We call this effect aliasing.