9.1 MATHEMATICAL ELEMENTS
There are a number of rotational elements that will create torques,
We can also consider the energy and power in a rotational system
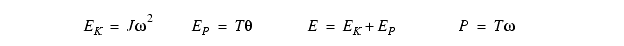

9.1.1 Inertia
Rotational inertia is a function of unbalanced torques, and the polar moment of inertia. This gives rise to another form of d'Alambert's equation.
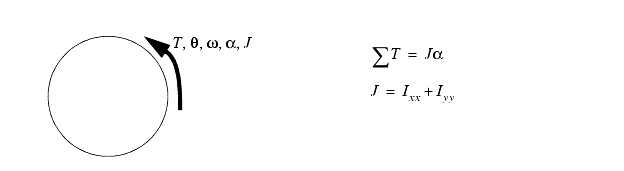
The rotational inertia is about the center of mass and will be oriented in the negative rotational direction. (Therefore it is on the opposite side of the sum of torques equation)

9.1.2 Springs
Rotational springs are commonly found in products like measuring tapes and children's toys.
Essentially springs behave like members under torsion.

We can use Hooke's law to deal with an engineered torsional spring.

Note: the angles used should be in radians.
As long as the spring is deforming elastically the results will be valid. When it deforms plastically the spring constant value will probably increase, and the undeformed position will change.
9.1.3 Viscous Friction
As before we can assume that some viscous liquid exists between two rotating shafts. The torque this viscous barrier will exert will become higher as the velocity increases.

If the viscous boundary is between two moving surfaces, then the difference between the two will determine the torque.

These calculations should be done using radians as the units.

9.1.4 Levers
A lever is a simple device used to balance moments in a system.
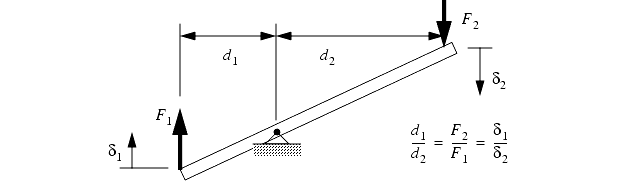
These are very common in engineered systems.
These are well behaved when the displacements are small.

9.1.5 Gears and Belts
Gears act as solid connections between mechanical components.
Gears come in a variety of shapes, but all of these transmit forces at a fixed radius.
The contact forces between the gears are always equal and opposite. The forces are also tangential to the pitch radius of the gear.
Gears will typically have different radii to create a mechanical advantage. This also results in a ratio between angular motion. The number of teeth on a gear is proportional to the diameter.

Quite often we will have a sequence of gears to give a significant gear ratio in a compact space. We will also have gears that can be engaged different ways to get multiple gear ratios, such as standard transmissions in cars.
If we have a rack and pinion gear set (a straight rack gear) then we convert rotational motion to translational motion.

When dealing with belts in system we use the same principles as with gears (except there are no teeth).
