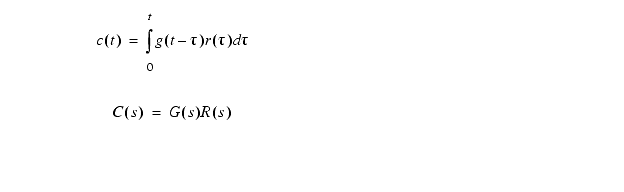16.1 THE LAPLACE TRANSFORM

---

The Laplace transform allows us to reverse time. And, as you recall from before the inverse of time is frequency. Because we are normally concerned with response, the Laplace transform is much more useful in system analysis.

The basic Laplace transform equations is shown below,

Consider the examples below,

16.1.1 A Few Transforms

The basic properties Laplace Transforms for are given below,

A set of useful functional Laplace transforms are given below. These are mainly used for converting to and from time 't' to the Laplace 's'.

16.1.2 Impulse Response (or Why Laplace Transforms Work)

Consider a system model. That model can be said to have an input (forcing function) and an output (resulting response function).

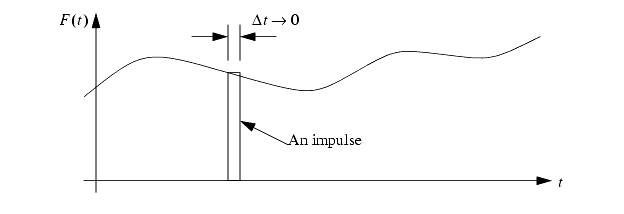
If we look at an input signal (force here) we can break it into very small segments in time. As the time becomes small we call it an impulse function.

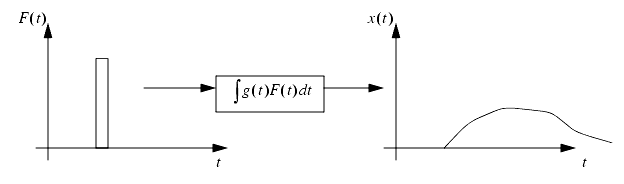
If we put an impulse into a system the output will be an impulse response.

If we add all of the impulse responses together we will get a total system response. This operation is called convolution.

The convolution integral can be difficult to deal with because of the time shift. But, the Laplace transform for the convolution integral turns it into a simple multiplication.