16.13 MORE PRACTICE PROBLEMS
1. Develop differential equations and then transfer functions for the mechanical and electrical systems below.
a) There is viscous damping between the block and the ground. A force is applied to cause the mass the accelerate.

2. The following differential equation is supplied, with initial conditions.
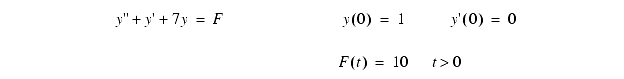
a) Write the equation in state variable form.
b) Convert the differential equation to the Laplace domain, including initial conditions. Solve to find the time response to the given input using Laplace transforms.
c) Solve the differential equation using calculus techniques.
d) Find the frequency response (gain and phase) for the transfer function using the Fourier transform. Roughly sketch the bode plots.
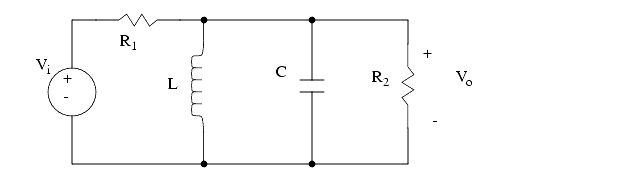
3. a) Write the differential equations for the system pictured below.
b) Put the equations in state variable form.
c) Use mathcad to find the ratio between input and output voltages for a range of frequencies. The general method is put in a voltage such as Vi=1sin(___t), and see what the magnitude of the output is. Divide the magnitude of the output sine wave by the input magnitude. Note: This should act as a high pass or low pass filter.
d) Plot a graph of gain against the frequency of the input.

4. Find the transfer functions for the systems below.
a) Vi is the input and Vo is the output.

b) Here the input is a torque, and the output is the angle of the second mass.
