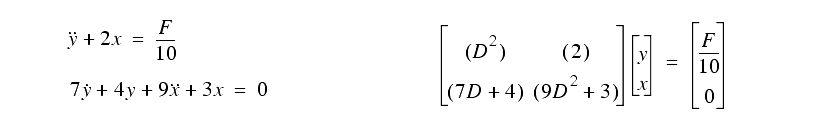6.7 PRACTICE PROBLEMS
������������
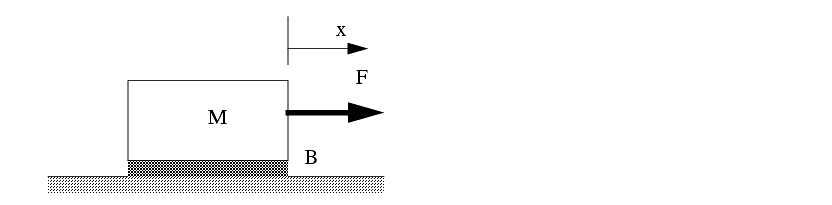
1. Develop the input-output equation and transfer function for the mechanical system below. There is viscous damping between the block and the ground. A force is applied to cause the mass to accelerate.
2. Find the input-output form for the following equations.
3. Find the transfer function for the systems below. Here the input is a torque, and the output is the angle of the second mass.
4. Find the input-output form for the following equations.
5. The following differential equations were converted to the matrix form shown. Use Cramer's rule to find an input-output equation for `y'.
6. Find the input output equation for y2. Ignore the effects of gravity.
7. Find the input-output equations for the systems below. Here the input is the torque on the left hand side.
8. Write the input-output equations for the mechanical system below. The input is force `F', and the output is `y' or the angle theta (give both equations). Include the inertia of both masses, and gravity for mass `M'.
9. The applied force `F' is the input to the system, and the output is the displacement `x'.
a) Find x(t), given F(t) = 10N for t >= 0 seconds.
b) Using numerical methods, find the steady-state response for an applied force of F(t) = 10cos(t + 1) N ?
c) Solve the differential equation to find the explicit response for an applied force of F(t) = 10cos(t + 1) N ?
d) Set the acceleration to zero and find an approximate solution for an applied force of F(t) = 10cos(t + 1) N. Compare the solution to the previous solutions.
10. Find the transfer function for the system below.
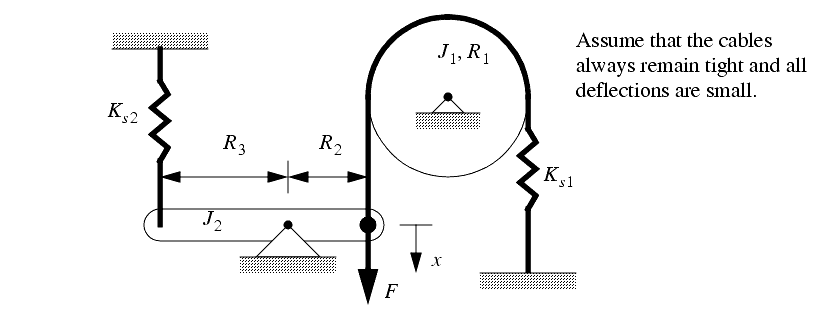
11. For the system below find the a) state and b) input-output equations. The cable always remains tight, and all deflections are small. Assume that the value of J2 is negligible. The input is the force F and the output is the angle `theta'.
12. Find the input-output equations for the differential equations below if both 'x' and 'y' are outputs.
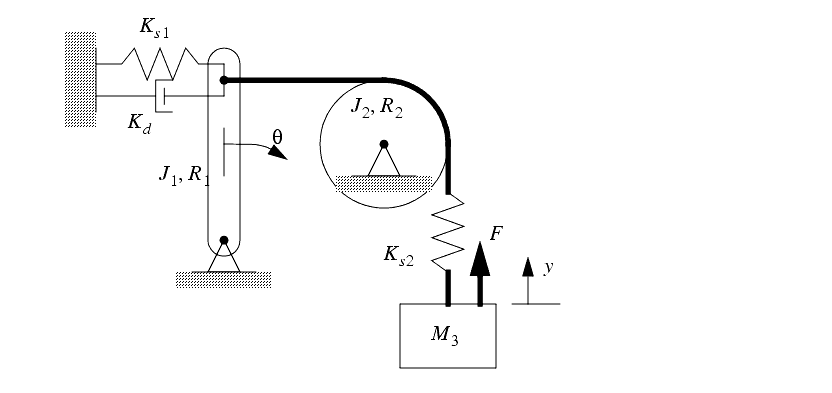
13. For the system pictured below find the input-output equation for y2.