20.2 OBSERVABILITY

---

- a system is observable iff the system state x(t) can be found by observing the input u and output y over a period of time from x(t) to x(t+h).

- If an input is to be observable it must be detectable in the output. For example consider the following state equations.

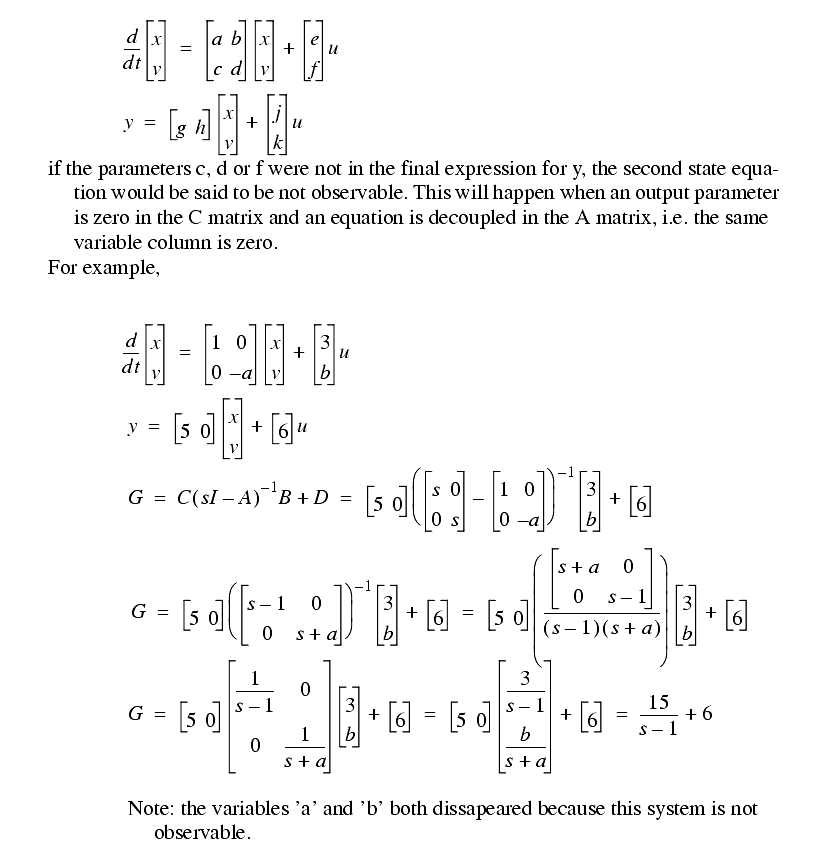
This often happens when a system has elements that are decoupled, or when a pole and zero cancel each other.

Observability can be verified formally for an LTI system with the following relationship.

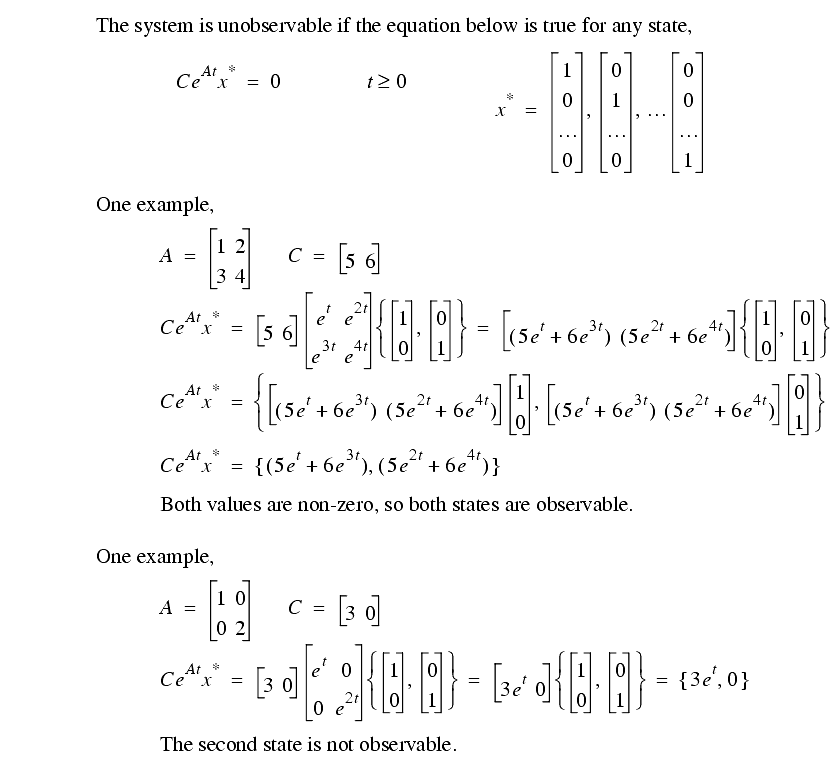
Another theorem for testing observability is given below. If any of the states satisfies the equation it is unobservable.

Yet another test for observability is,

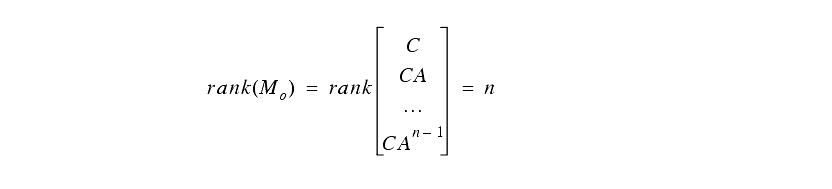
If a system in unobservable, it is possible to make it observable by changing the model.

A pole-zero cancellation is often the cause of the loss of observability.

If all unstable modes are observable, the system is detectable.