35.9 z-TRANSFORMS

---

For a discrete-time signal , the two-sided z-transform is defined by . The one-sided z-transform is defined by . In both cases, the z-transform is a polynomial in the complex variable .

The inverse z-transform is obtained by contour integration in the complex plane . This is usually avoided by partial fraction inversion techniques, similar to the Laplace transform.

Along with a z-transform we associate its region of convergence (or ROC). These are the values of for which is bounded (i.e., of finite magnitude).

Some common z-transforms are shown below.

Table 1: Common z-transforms

Signal	z-Transform	ROC
	1	All

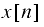
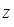
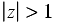
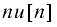
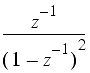
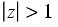
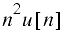
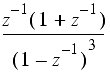
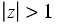
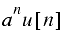
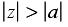
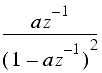
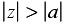
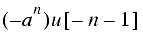
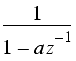
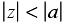
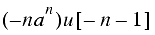
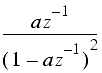
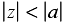
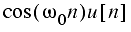
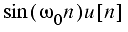
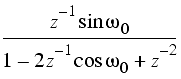
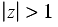
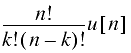
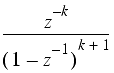
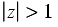
The z-transform also has various properties that are useful. The table below lists properties for the two-sided z-transform. The one-sided z-transform properties can be derived from the ones below by considering the signal instead of simply .

Table 2: Two-sided z-Transform Properties

Property	Time Domain	z-Domain	ROC
Notation
Linearity			At least the intersection of and
Time Shifting			That of , except if and if
z-Domain Scaling
Time Reversal
z-Domain Differentiation
Convolution			At least the intersection of and
Multiplication			At least
Initial value theorem	causal