
• an approximation for sound propagation is a sphere as a wavefront.

• an ideal sound wave travels as a uniform wave in a radial direction (thus having uniform distribution over the sphere). If we watch the pressure at point ‘P’ as a single sound wave (soliton) travels by, it will look like,

• The wave equation for sound in air is given below,

• If a sound is a pure tone, it will look like,

• For air the speed of sound can be approximated with,

• Velocities in other materials (at 21.1°C) are, [Source Irwin and Graf]

• Sound powers cover such a wide range that it makes sense for the values to be expressed in a logarithmic scale, a few values are given for reference. Note: this value measures the sound source itself, not what the listener hears. [source Irwin and Graf]

• The sound power level is useful when considering the source, but as we move farther away from the source the sound pressure our ears can detect will drops off. Another logarithmic scale can be used to express power levels we hear.

• recall that log (or dB) values can’t be added directly, they must be converted back to normal values first.


• Obviously averaging values must observe the same restrictions as addition,


• Previous discussions centered on simple sound measurements, but actual machines are more complicated.
• Sound levels are unequal in different directions.

• The unequal distribution of sound energy can be expressed with a directivity factor,

• A directivity Index can be helpful when the directivity factors have a wide range

• It is impossible to measure sound at all points around a source, so some points must be selected.
• One technique is to divide the surface of the sphere into a number of flat polygons.

• It is best to have an anechoic environment
anechoic: an environment that (effectively) eliminates reflected noise.

• In some cases only half of the measurement sphere can be used because of object size, or requirements.

1. Select number of points to measure
2. Get list of points by selecting measurement radius, and with point table (only the top half is a hemisphere)
3. Measure sound pressure at each point (Lp)
4. Correct for points on plane if half sphere
5. Find Lp (correct for -3dB if hemisphere)
6. Find Q or DI for each point is required
• The human ear does not hear all sounds as equal.
• One simple measure is the ‘phon’, it is based on experimental data. (Note that Lp = phon at 1KHz). [Source Irwin and Graf]


• Another measure that is adjusted for loudness is the ‘sone’. This compensates for what we would consider a perceptual loudness level.


• As we saw before, sound is made up of a variety of frequencies, so we must determine how all of the components are combined into a single value.


• The loudness index contours are given below. [Irwin and Graf]


• We can use a similar method for the perceived noise level using the ‘noys’ graph below, and use this in place of the graph in the previous method. [source Irwin and Graf]

• The previous measurement methods are suited to measuring for specific noise sources, but there is also ambient background noise.
• Noise Criteria Curves, use the given curves for Noise Criteria (NC) or Preferred Noise Criteria (PNC) [Source Irwin and Graf]


• To use the curves, plot on values, and the highest NC curve that is touched is the NC level

• There are some basic suggested levels for background noise indoors,

• Previous methods use graphical techniques to adjust sound response.
• We can also use an adjusted weighting [source Irwin and Graf]



• A simple measure to estimate interference with human speech is the Speech Interference Level (SIL) and more recently the Preferred Speech Interference Level (PSIL)

• The values can be correlated to speech levels and distances that they may be heard at, [Source Irwin and Graf]


• WHY? to give formal standards so that engineers can guarantee excessive limits are not exceeded. Without formal numbers, we could “bend-the-rules”
• The Occupational Safety and Health Act of 1970 (USA)
can be measured with device attached to worker for a period of time (these measure total sound exposure).
safe exposure levels [source Irwin and Graf]

When calculating, consider that noise levels change all day long,


• A table of international acceptable noise levels is given below (from [Hay, 1975])

• Typical requirements for exposure to noisy environments

• From the Noise Control Act of 1972 (USA) a basic procedure was developed for estimating noise exposure for the general public.
• Given a number of noise readings at the perimeter of a facility over a day, find the noise levels.



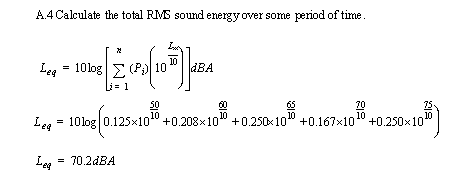







• The American EPA developed some suggested noise levels. A list (of one at this point) is,


• will be covered later, but for now we want to determine how much sound pressure they are creating at different frequencies.

• The measurements are done most often in imperfect environments (perfect environments discussed later)




• Convert sound pressure to electrical signals

• A microphone has a finite area to measure the sound with. As the diameter ‘d’ approaches the wavelength of sound, the sound becomes distorted.

• When wind blows across a microphone, it generates a low frequency turbulence noise. This is often corrected by using dBA measurements, and foam balls.
• Corrections must also be made for changes in temperature and altitude


• Signal spectrum is a fundamental concept, these machines allow us to measure this
• Some possible spectrums are,



• Filters can be designed using Bode Plots. These filters can reduce or increase the amplitudes of input frequencies in certain ranges.


• Octave band analyzers (and others) are mainly distinguished by the difference between the upper and lower cutoff frequencies.

• The narrower the bandwidth of the analyzer, the more expensive the instrument
• octave, 1/2 octave, and 1/3 octave analyzers are more common.
• The analyzers so far only look at specific frequencies but we can use them to look at a variety of frequencies.

• A typical mode of operation for older analyzers requires some interpretation. The graph is drawn by switching each channel on for a short period of time, the voltage from a certain frequency band is plotted (this allows variations at that frequency to be seen). After some period of time the center frequency is shifted to another value. This means the bands are wider for an octave analyzer, or the bands of the analyzer are narrower for a 1/3 octave bandwidth. The wider bands hide noise when using wider bandwidths. For example the peak near 200Hz is more obvious with the 1/3 octave analyzer. The noise appears to be a multiple of 60 (3 * 60 = 180), suggesting that it is the motor speed, driving a geared up impeller.
• Noise is generated by some common methods

• Estimation factor for noise generation [source Irwin and Graf]

• There are other sources that are noisy, but not suited to simple factors,
• A table of relationships for common equipment is given, [Irwin and Graf]


• Some general levels of sound power for industrial equipment are given below for frequency ranges from 500-4000Hz.


• Sound levels are given below that are typically generated by home appliances (500 to 4000Hz)

• The basic idea is to determine how sound energy is distributed, absorbed and reflected in a closed space.

• Sound is absorbed by walls, floors, etc.

• the ‘α’ absorption coefficients are determine experimentally, and can be found in the table below, [sources ??????]


• The absorption coefficient ‘α’ for a room can be calculated using the ‘α’ for each surface,

• ‘α’ can also be corrected for temperature and humidity using factors in the table below,

• previous assumptions were based on rooms with uniform power distribution, but this is not the case.

• Sound pressure is more useful than energy density, and happens to be quite similar in formulation.

Step 1: Measure sound on surrounding sphere,
over frequency ranges, e.g. octaves 31.5, 63, 125, 250, 500Hz
Step 2: Calculate R (via α) or experimentally with sound decay equation from before
Step 3: Calculate sound power level for each measurement position, and each frequency with,

Step 4: Calculate Lw for each frequency band.

• Estimation of R from sound decay is based on equations,

• When sound reflects off a flat surface it keeps the same spherical surface, but the center of propagation is mirrored across the reflecting surface. Like light the angle of incidence is equal to the angle of reflection.

• When the sound is incident on a narrow slit or edge, it regenerates, as if the slit is a new source.

• various other combinations of openings in wall, and half slits produce different sound propagation patterns.
• Previous notes concentrated on sound from local sources
• But, another class of problems involve walls, and barriers between sound sources, and listeners.
• The effects of walls are measured as a Transmission Loss (TL)

• Barrier Transmission Loss is a function of frequency

Wall stiffness region: hard to predict exactly, the stiffer the wall, the greater the TL. Resonances in this region are a function of structure.
Wall Mass Region: The mass of the wall controls sound transmission [source Irwin and Graf]

Coincidence Region: (not common) Sound waves hit wall at angle: effectively changing frequency. Because of the lowering of the high frequency to a lower value, the wall can now be excited.
• A table of TL values for walls are, [source ????????]

• Another list of transmission loss figures is given below for typical building materials, [source ???????]

• A table of typical NR values for walls are, [source ??????????]

• The Sound Transmission Class (STC) is the Transmission Loss (TL) at 500Hz
• We can use the transmission loss of the wall to estimate sounds heard in adjoining rooms.

• Sometimes wall are built up of layers to improve sound absorption

• Most walls have areas covered by different materials. When this is the case we can combine the coefficients

• Holes in the wall will increase the sound that is transmitted, but these are often needed for wires, airways, etc. Offsetting holes can help maintain sound isolation properties.

• Another problem with sound isolation is that other paths may be ignored. For example a barrier may be built between two rooms, but raised floor is ignored, and sound continues to travel through this route. Other well known sound paths are ventilation ducts.
• Hoods are a common method of dampening noises

• The NR and TL are for reduction of the new reverberant field Lp1, but we are concerned with the reduction of Lp0. This is the Insertion Loss (IL).

• The noise reduction for hoods is very good at higher frequencies Isolation pads can be used to reduce the noise at lower frequencies. When used together the total noise levels will be decreased.
• Sometimes barriers (or free standing walls) can be placed in the direct path of the sound.

• In effect we can increase absorption in a room by adding suspended additional surface area.
• suspended panels can flex, best absorption characteristics at low frequencies. typical values for alpha are .2 to .5 for 125Hz.
• These can be tuned for specific frequencies
• Locating these absorbers next to a wall with absorbing material will increase high frequency absorption.
• Typical materials are glass, plywood, metal.
• Noise Reduction Coefficient (NRC) for a material takes care of frequency dependence of absorption

• For reduction of reverberant noise we can use a Noise Reduction (NR) coefficient

• An addition to a sound pathway can reduce the sound levels that pass. These are commonly used with internal combustion engines to reduce sound, along with other devices. An example of muffler systems is given below,

• After the fan there is typically a length of 5 to 10 diameters to allow the flow to settle. This makes the fan more efficient, and reduces noise from fan turbulence. This length between elements will also help improve performance.
• Absorbs a portion of the sound
• The more material, the better these devices absorb sound. Typical materials include mineral wool, and may use a stainless steel or mylar cover to protect the materials from high velocities and corrosive gases.

• These are good at high frequencies.

• Typical duct liner sound absorption characteristics are given below,

• As sound must turn corners, it attenuates.

• For a 90° bend in a pipe we can expect attenuation as given below. These numbers assume that the bend section is round or rectangular with the diameter or widest dimension being that given. A lining is assumed with a thickness of 10% of D.

• For a 180° bend we can find the attenuation by looking at the absorption coefficient, diameter of duct, and length of bend section.

• An offset in a pipe of the right dimensions can reduce the sound well. The plenum itself is a large volume compared to the duct.
• The reduction is a function of both the absorption and reflection path.
• Typical attenuations are 10 to 20 dB.

• When a particular frequency of sound is to be muffled, a tuned cavity can be used.
• These use a change in impedance at the inlet and outlets.

• Another type of tuned resonator is a Helmholtz resonator.
• This is basically a cavity added onto the side of a pipe.
• The air inside the cavity acts as a spring. When the quantity of air is a specific volume, it will resonant with a specific frequency.
• These are typically best at low frequencies.
• The device can be used at higher frequencies, but it is typically lined with fiberglass or other porous materials.

• Thanks to John Lea for pointing out needed material the fist time I taught this course.
• Thanks to Paul Short for giving me feedback on these notes, and pointing out a number of errors.
Problem 20.1 What is the frequency of a wave with a wavelength in air of 0.026m at 10°C (in air)?
Problem 20.2 What is the sound power radiated by a machine with specified sound power level (Lw) of 130 dB?
Problem 20.3 Three machines of equal sound power are to be placed next to two existing machines each having sound power levels of 82dB. It has been determined that the combined sound power of all 5 machines must not exceed 63mW. What maximum sound power level must each of the new machines be limited to?
Problem 20.4 A cylindrical tube is to be used for sound propagation tests with a loudspeaker located at one end pointing down the tube. The range of test frequencies to be examined is from 300Hz to 3000Hz under temperature extremes of 5 degrees Celsius to 25 degrees Celsius. Determine the minimum tube length to ensure one full wavelength at the lowest frequency and the maximum diameter to limit the highest frequency transverse (across the tube) wave to one half wavelength. The above to hold for all temperature extremes.
Problem 20.6 The following data was recorded for a non-isotropic source. What would be the directivity factor (Q) in direction θ = 60° (use appropriate approximation for calculation of the average value).
Problem 20.7 You are given two loudspeakers to be mounted in the passenger section of a commercial aircraft. For testing, a speaker is mounted in a test setup, and powered with a 40 watt stereo. Measurements are taken at the points listed below. From the data, a) calculate dB pressure level for each measurement, b) calculate directivity for each point, c) calculate the total power, and d) select the speaker best suited to the application (or neither) and explain your choice.

Problem 20.8 What will be a) the total sound power level of 5 machines rated as follows 93dB, 91dB, 89dB, 92dB, 88dB. b) If the least noisy machine is turned off, by how much does the dB power level drop?
Problem 20.9 Three machines are individually measured against a background level of 78 dB. Sound pressure levels are 83dB, 81dB, 80dB. What would be the total sound pressure level with all three machines on at a new location where the background level was 80dB?
Problem 20.10 Calculate the average sound pressure levels for the following recorded values: 89dB, 93dB, 97dB, 85dB, 92dB.
Problem 20.11 Two identical sources have a combined amplitude (Lp) of 104dB. What would be the value of the root mean square pressure for just one of the sources?
Problem 20.12 The sound pressure level measured at a distance of 3m from a machine including background noise was recorded as 96dB. The ambient level was then measured with the machine off and found to be 93.4dB at the same location. If the ambient level was to be raised by 2dB what would the combined machine and background level at the same measurement location?
Problem 20.13 Given a set of three sound pressure measurements (.05Pa, .03Pa, .04Pa) taken at 1/2 Octave intervals, starting at 200 Hz, find the total loudness in sones.
Problem 20.14 A machine has a loudness rating of 35 sones, what will be the loudness level (phons): give approximate (graphical) and exact (calculated) answers.
Problem 20.15 Based on a limited one octave (1/1) analysis calculate the loudness in sones for the following noise and loudness level

Problem 20.16 You have been approached by a business that has just signed a 5 year lease for office space. But, they want to cancel the lease because they claim the background noise is too great for an office. You enter the building and take some readings at every octave from 100Hz. The values you get are 35dB, 42dB, 48dB, 42dB, 35dB, 31dB. Is the sound level suitable for office space?
Problem 20.17 For the same spectrum as in #S15, calculate the NC rating (use the graph).
Problem 20.18 Using the graph to calculate the total level in dBA for the same spectrum. Use fig 2.8 (A-weighted curve) to find dBA levels then add.
Problem 20.19 You have decided to quit engineering, and go into the restaurant business. And, your new concept is to design an environment where the patrons don’t have to shout. You are using 5 foot round tables throughout the room, with a 1000W sound system that gives even music throughout your establishment. a) Calculate the general range of pressure levels from 500Hz to 2000Hz that would interfere with shouting. b) Calculate the general range of pressure levels from 500Hz to 1000Hz that would interfere with normal speech.
Problem 20.20 The sound pressure readings below were taken at 1/3 octave intervals beginning at 500 Hz; 54, 72, 89, 87, 92, 94, 95, 104, 88, and 74 dB. These readings were taken in the same room that houses 3 workers. We must determine if the room sound levels are safe.

a) Calculate the loudness index.
c) Calculate the total pressure Lt.
e) What is the farthest distance apart and two workers may be to hear each other shouting using PSIL and background dBA?
f) What is the maximum safe exposure time allowed in this environment each day?
Problem 20.21 The Shoutalot Sound Measurement Company was hired to determine if an assembly shop was safe for the workers at the Rustyheap Car Company. To do this they took sound measurements and found that the workers were right at the safety limit (i.e. D = 1). But before the report was completed, Mr. I.M. Kluzt, P.E., lost the sheets of paper that the measurement data was on. But he remembered that 3 hours of the 7 hour shift are at 95 dBA. You must estimate what the sound level was for the other 4 hours of the shift (the additional 4 hours were all at the same level).
Problem 20.22 At the perimeter of a local fast food restaurant you find the noise levels are 60dBA from 2am to 8am, from 8am to 8pm the noise level goes up to 75dBA, and from 8pm to 2am the noise level goes down to 70dBA. Assuming this has a 10 dBA night-time noise penalty from 10pm to 7am, calculate the noise pollution level.
Problem 20.23 a) A worker has been exposed to noise levels over a period of 5 hours as listed below. For what remaining portion of his 8 hour shift could he be exposed to a level of 90 dBA.

b) Based on a daytime Leq of 60dBA and a nighttime level of 45dBA, what would be the Ldn index for the entire day? (ans. 58.7dBA)
Problem 20.24 The sound spectrum below is known to exist for an industrial machine. Keeping in mind the proximity of some of the peaks, what bandwidth would our sound instrumentation require to tell them apart?

Problem 20.25 For a 1/12 octave band pass frequency analyzer what would be the percentage (B.W./f0) and the upper and lower cutoff frequencies at f0=12000Hz.
Problem 20.26 A 1/10 octave bandpass filter has a center frequency of 5000Hz. Calculate the half power bandwidth cutoff frequencies (f1, f2) and the local attenuation of a pure tone signal at 6000Hz by this filter.
Problem 20.27 The Bouncy Rubber company uses a 100 horsepower air compressor and an exhaust fan when making vulcanized rubber balls. The axial fan creates a flow of 5 m3/sec at a pressure of 200 mmHg. The (10’ by 10’ by 10’) room they are housed in has walls of concrete blocks painted red.
a) Calculate the acoustic power generated by both machines.
b) Calculate the absorption coefficient of the room.
c) Find the sound energy density of the room and compare the direct and reverberant components.
d) Calculate the longest duration a worker may stay in the room.
e) Suggest a new room coating to reduce the sound levels to allow 8 hour work days.
Problem 20.28 A generator room contains an average 500 h.p. diesel motor (the sound is about 1000Hz). The ceiling and walls of the (3m by 3m by 3m) room are covered in plaster and the floor is concrete. On one wall there is a 2m by 2m window. If the generator is in one corner of the room, and you are in the other corner, what sound pressure will you hear (in Pascals)?
Problem 20.29 Acoustic Ohm’s law for freely propagating states that,

a) Derive the equation which specifies

b) evaluate the unknown (?) expression given,

Problem 20.30 A machine is located at position A and radiates 0.6W of sound power in the octave band centered at 1000Hz with a directivity of 1.6 in the direction of an observer at location B. The machine is operated for each 8 hour shift. There is a second machine located at position C which is used infrequently. It radiates a sound power of 0.2W with a directivity of 1.0 in the same frequency range.

a) calculate the total direct sound pressure level at position B with both machines on (i.e., ignoring the reverberant field effects).
b) calculate the average absorption coefficient and the room constant in this frequency range (use the table in the notes for component values).
c) calculate the sound pressure level at position B with only machine A on taking room effects into consideration.
Problem 20.31 The company would like to reduce the sound pressure level at the operator location and is considering laying foam backed carpet (α = 0.69) on 75% of the floor surface. What would be the new sound pressure level at position B, machine A on under these conditions.
Problem 20.32 Predict the expected sound pressure level at a location 3m from a source radiating 100dB of sound power, assume isotropic radiation (spherical) and in a sound absorbing room. If the actual reading at this location was 83dB, what would be the Directivity Factor (Q) be?
Note: the equation you use in the first part of this question is derived from the relationship (i) the directivity of the source modifies the numerator of this expression (ii).

Problem 20.33 Under free field conditions the sound pressure level of a noise source was measured and found to be 88dB at a distance of 4m. Assuming isotropic radiation what would be the sound power level (Lw) of the source?
Problem 20.34 a) If an enclosure was made from 3/4” thick plywood to fit over the noise source in S30, what internal treatment would be required to ensure an insertion loss of 21dB.
b) For the room described in S30 assume acoustic treatment is applied to raise the average absorption coefficient to 0.40. What time would be required for the sound energy density to reach 60% of it’s steady state value after the machine was switched on?
c) A noise source is located in anechoic free space and emits 1.5W of sound power. A sound level meter is located 3m from the source and the directivity factor in this direction is 4. Calculate the expected sound pressure level and derive the average sound pressure level at a radius of 3m from the machine.
Problem 20.35 The Boris and Natasha Detective Agency has hired you to build soundproof walls between their interrogation rooms. The dimensions and location of the two rooms are shown below. The loudest voice in either room will be 80dB, and a listener can hear voices at pressure levels above 20dB. What materials should be used for the wall?

Problem 20.36 In another study the company decides to investigate the benefit of making a separate room to contain machine A and program machine B to run unattended after hours. A door between the two rooms would not be necessary, however a 1m by 2m window is considered essential (this would be heavy plate glass to reduce transmission losses α=0.03 and TL=40dB at 100Hz). The broken line shows the intended separation line which would be a 2” by 4” stud wall with 0.5” (6 lbs/ft) gypsum panels on both sides (α = 0.05 and TL = 40dB at 1000Hz). What would be the new sound pressure level at position B with the machine on and the wall in place. Assume reverberant field conditions (Lp3).
Problem 20.37 The room pictured below is made from standard construction materials as noted. The machine radiates 2W of acoustic power isotropically in the octave band centered at 500Hz.

a) calculate the steady state space average sound energy density for the room.
b) what will be the sound pressure level at position #1?
c) without doing the actual calculations, explain how you would go about determining the sound pressure level at point #2, just outside the exterior west wall.
Problem 20.38 (See figure below) The elevation and plan views of a room are shown. A barrier is to be installed. The location and height have been determined. The required insertion loss considering diffraction paths only is to be 5dB. The absorption coefficients in the octave band centered at 500Hz are .70, .30, .05 for the ceiling, walls and floor respectively. The printer generates a sound power level of 110 dB and in the direction of the worker location has a directivity factor of 1.9. Calculate the barrier length necessary to ensure the required insertion loss

Problem 20.39 You think that a bend in a narrow hallway of your house reduces noise levels. This “plenum” has the dimensions below. Determine the Transmission Loss for 500 Hz.

Problem 20.40 For the same noise in #S15 calculate the total perceived noise (PN) and perceived noise level (PNL)

Problem 20.41 The S.Butts Manufacturing company produces large castings. Seymour, the division director has asked that the Engineering department take sound readings about a large machine. The engineers make the following measurements with the machine turned off, then on.

a) Correct for the machine on/off.
d) Find the directivity values.
e) What level of our perception would we say this is equivalent to? (e.g. whisper)
Problem 20.42 A large incinerator is located in the center of a residential neighborhood. Inside the facility the measurements are made of general background noise, these are listed below. Measurements are also made outside over a 24 hour period at the perimeter of the facility.

a) Find the inside values in phons and sones, and find the total loudness.
b) Find the A weighted values and calculate the total pressure.
c) How far apart would two employees have to stand to hear each other shouting?
d) How many hours a day could a worker safely be in the work area?
e) If the local municipality has an 11pm to 6am noise penalty of 15dB, what is the noise pollution level, and the Ldn?
Problem 20.43 A room, 8’ high by 10’ by 20’ has painted concrete floors, painted concrete walls, and an unpainted concrete ceiling. If a 100hp electric motor (1200rpm) is in one end of the room,
a) What is the general sound level in the room?
b) Design a wall to divide the room so that on the side without the motor the sound is 20dB lower.
c) Instead of a wall as in b), design a hood to sit over the motor.
Problem 20.44 We take measurements about a sound source and get the following table (except the missing value). Using the following relationship, and the table of values, find the missing value.

Problem 20.45 A sound is measured in octave intervals starting at 115 Hz. The pressure level values measured (in order of frequency) are given below. Find the total loudness in noys. (for octaves K= 0.3)
Problem 20.46 A recent observation has revealed that an older type of beverage, commonly known as a ‘shooter’, has become popular in an previously unexplored market. As a result you decide to cash in on the trendy new happening and cater to this niche market. To keep the patrons drinking, you plan to play the music loud, but if it is too loud the waiting staff will not be able to hear the somewhat intricate orders. You have decided that in the worst case the patron will have to shout over a maximum distance of 3 feet. Tests on the music system reveal that the sound has a fairly constant level, except near 1000 Hz, where it always seems to be 20dB above all of the other frequencies. If we set the volume level of the music system using a sound pressure meter that is set to 500Hz, what is the ideal reading on the sound meter?
Problem 20.47 A design is specified so that it should have a maximum preferred noise criteria value of 35. When tested, the sound values measured at half octaves from 63Hz are,
41dB, 43dB, 46dB, 51dB, 48dB, 48dB, 35dB, 33dB
At what frequencies are the sounds measured above tolerance, and which sound frequency is the worst violator. Use the graph and clearly indicate how you arrived at your solution.
Problem 20.48 The S.Butts Manufacturing company produces large castings. Seymour, the division director has asked that the Engineering department take sound readings about a large machine. The engineers make the following measurements with the machine turned off, then on.

a) Correct for the machine on/off.
d) Find the directivity values.
e) What level of our perception would we say this is equivalent to? (e.g. whisper)
Problem 20.49 A large incinerator is located in the center of a residential neighborhood. Inside the facility the measurements are made of general background noise, these are listed below. Measurements are also made outside over a 24 hour period at the perimeter of the facility.

a) Find the inside values in phons and sones, and find the total loudness.
b) Find the A weighted values and calculate the total pressure.
c) How far apart would two employees have to stand to hear each other shouting?
d) How many hours a day could a worker safely be in the work area?
e) If the local municipality has an 11pm to 6am noise penalty of 15dB, what is the noise pollution level, and the Ldn?
Problem 20.50 A room, 8’ high by 10’ by 20’ has an unpainted concrete floor, painted concrete block walls, and an unpainted concrete ceiling. If a 100hp electric motor (1200rpm) is in one end of the room and whines at 990Hz,
a) What is the general sound level in the room?
b) Design a wall to divide the room so that on the side without the motor the sound is 20dB lower.