
• In addition to basic statics this topic will lead in to estimating strengths of beams, dynamic behavior, mass, etc.

• A simple way to illustrate the moment arm effect of gravity about a centroid is by considering an exaggerated T shape that is supported by two cables, one at either end.



• A note of interest, when the object is symmetrical the center of mass and centroids will be the same. Another term of significance is the center of gravity, but unless we have a part with a significant gravity gradient across it, this will be the same as the center of mass. Unless dealing with very sensitive equipment, or astronomically significantly distances, the center of gravity, and center of mass can be considered equivalent.
• This property is simply the point at which the mass on one side of the point is equal to the mass on the other side of the point.
• This property can be found with a summation of mass, weighted by distance.


• A simple example can illustrate the calculation of this property. A 2D example is given, but extension to 3D is trivial.

• Consider the example of the T-shape from before,

Problem 7.1 The 500 Kg plate below is to be used in an industrial machine. The basic shape is rectangular, but there is an angled arch cut in the bottom. Considering the centroid, and the applied force, determine the magnitude of the force (P) that is required to pull out the wedge if the both sides of the wedge have a coefficient of friction of 0.2.

• This is also known as the geometric center, or first moment of area.
• The fundamental definition for Centroids is given below, although a more efficient method for problems with simple geometries is discussed later.

• When finding centroids, look for symmetry, the centroids will be in the center of symmetrical sections.

• A simple example of application for these relationships is given below,

• Lets try a more practical problem using the centroid, ([Hibbeler, 1992], prob. 9-16, pg. )


Problem 7.2 We want to design two similar supports for a new sculpture. This means that the supports should be positioned to carry the same load. Find the distance of the second support from the first, and indicate the loads to be supported by each if the plate weights 1000kg per square meter.
• This method basically uses tables, or obvious centroids for basic shapes in a complex shape. By using a summation of centroids, weighted by areas/volumes divided by total area.

• A simple example for a two dimensional problem is given below, ([Hibbeler, 1992], prob. 9-48, pg. )

• Next, lets consider a problem using the composite method in 3D volumes, ([Hibbeler, 1992], prob 9-68, pg. )

Problem 7.3 An object is perched on the far end of a lever and we want to determine if it will tip, or slip off, or remain in place if the coefficient of friction is 0.2. (Note: the 2m distance to the right is to the centroid of the block)


• We will often encounter distributed forces in real problems. For the convenience of calculation we want to simplify these to point forces.

Problem 7.4 Find the reactions at the supports of the beam below if iron rods are piled as shown. Each 1” dia. rod weighs 30 lbs. The beam that the rods sit on weighs 2000 kg.

• An example of a roughly distributed load can be seen below,
• If we take some curve and rotate it about some axis, it will sweep out a shell of some volume. We refer to this as a Volume of Revolution.
• We can calculate the surface area of these shapes using the centroid and the arc length of the curve,

• We can easily calculate the volume of these shapes using the centroid and the area under the curve,

• These methods can be of particular interest when the shapes are difficult to integrate in three dimensions, or when we start with a profile of a shape. One example of this would be a program to drive a CNC lathe.
Problem 7.5 Find the volume of the toroid to the right if the minor radius is 3”, and the major radius is 5”

Problem 7.6 The plate below has a triangular hole. We are asked to select a base width ‘b’ for the triangle so that the reaction at roller B is 200N. The plate material weighs 1Kg per square meter.

Problem 7.7 The 500 Kg plate below is to be used in an industrial machine. The basic shape is rectangular, but there is an arch cut in the bottom. Considering the centroid, and the applied force, determine the magnitude of the force (P) that is required to pull out the wedge if both sides of the wedge have a coefficient of friction of 0.2.

Problem 7.8 A thin flat plate is suspended by means of a screw eye and 2 cords, AC and BC, as depicted in the diagram below. Given that the plate has a mass of 30kg per square meter of surface area, determine the reaction force at point O and the tension forces in the cords.

Problem 7.9 Find the x-y centroid of the shape below which is essentially rectangular, except for the shape cut out of the bottom (the function is given).

Problem 7.10 What is the x-y centroid of the shape below if the plate is homogeneous?

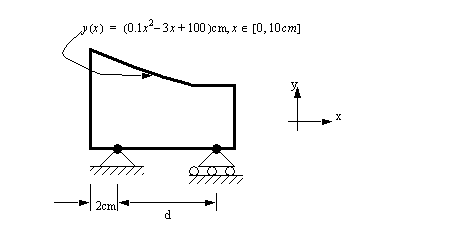
Problem 7.11 The mass below (a rectangle with a parabola cut out) is suspended by two cables with a diameter of 2mm. The cables have an undeflected length of 2m.

a) Find the x centroid for the plate and the force of gravity on the plate if the material weighs 50 kg per square meter.
b) Determine the new lengths of the cables at A and at B. Assume that the cables have E = 20GPa.
c) Based on the elongated cables, what angle does the plate sit at after it is released and deflects?