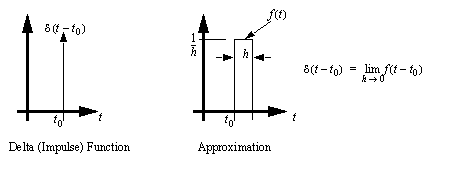
• An impulse function is a very (infinitely) thin but has a weight of 1. We can approximate this function with a finite width pulse. In both figures the delta function has been shifted in time.

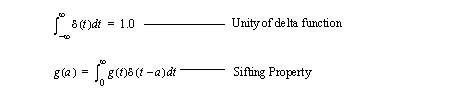
• Some of these basic properties are,
• Now consider a train of sample pulses with a regular interval T,

• The form derived above will allow a z-transform later.
• We can also recognize that if a function X(t) has a period less than the sample period ‘T’ then X*(t) will not be a reasonable sample of X(t). We call this effect aliasing.

• The basic definition for z-transforms is given below. And, like most transform methods, we assume that the initial values in the system are zero,

• Consider the z-transform shown below,
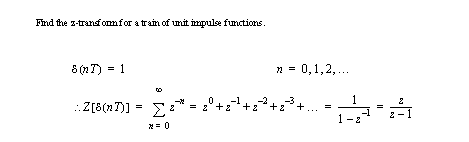
• We can do inverse transforms, much like we do inverse Laplace transforms,
