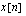 , the two-sided z-transform is defined by
, the two-sided z-transform is defined by 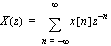 . The one-sided z-transform is defined by
. The one-sided z-transform is defined by 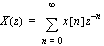 . In both cases, the z-transform is a polynomial in the complex variable
. In both cases, the z-transform is a polynomial in the complex variable 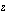 .
.
• For a discrete-time signal 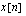 , the two-sided z-transform is defined by
, the two-sided z-transform is defined by 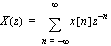 . The one-sided z-transform is defined by
. The one-sided z-transform is defined by 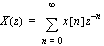 . In both cases, the z-transform is a polynomial in the complex variable
. In both cases, the z-transform is a polynomial in the complex variable 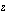 .
.
• The inverse z-transform is obtained by contour integration in the complex plane 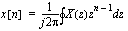 . This is usually avoided by partial fraction inversion techniques, similar to the Laplace transform.
. This is usually avoided by partial fraction inversion techniques, similar to the Laplace transform.
• Along with a z-transform we associate its region of convergence (or ROC). These are the values of  for which
for which  is bounded (i.e., of finite magnitude).
is bounded (i.e., of finite magnitude).
• Some common z-transforms are shown below.
• The z-transform also has various properties that are useful. The table below lists properties for the two-sided z-transform. The one-sided z-transform properties can be derived from the ones below by considering the signal  instead of simply
instead of simply  .
.