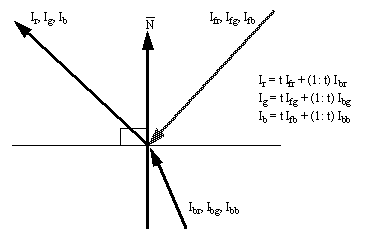Jack, H., Farmer-Haywood, M., "CS 488/533 Final Report on the Rubiks Cube Visualizer", University of Western Ontario, 1992
Rubik’s Cube Ray Tracing Software
1.0 Executive Summary:
This report involves the discussion of a user interface and ray tracing package for the display of a Rubiks Cube. The package was produced using only low level graphics calls. All high level functions, from transformations to ray tracing were written into customized algorithms. The final package comes in four modules: the User Interface; the Ray Tracer; and the Quantizer and Display Utilities.
The user interface performs real time animation of the Rubiks cube in three dimensions, and prepares the data format required by the Ray Tracer. It has been constructed with a control loop which recognizes flags and toggles. This loop is constantly executed, so that the user may make input without stopping execution of the animation graphics.
The Ray Tracer has been constructed to run in batch mode. The scene is read from a file, and the image is processed, and written to another file. This allows the user interface to be used while the graphics are being processed. The ray tracer incorporates both reflection and refraction. A checkerboard floor is also included for increasing the visual impact of the image. All of the Ray Tracing properties may be set from the User Interface program.
The image output from the Ray Tracer produces RGB intensities for each pixel. This must be converted to a limited color map for most machines. Thus a program to quantize the colors in the file has been written. The results from this process are also written to a file, and a Program has been devised to load the image and display it on a Sunview based display.
2.0 Specifications:
The objective of this project is to produce a package to aid in the visualization of a Rubiks cube. The program is to be easy to use, and provide both perspective views and ray traced images.
2.1 Hardware Requirements:
• The User Interface, and the Display programs both require a Color Sun Computer
2.2 Software Requirements:
• The User Interface, and the Display programs both require Sunview.
2.3 User Interface Features:
• Displays a Rubiks Cube in 3D perspective,
• Allows variations to all viewing parameters on-screen, or with controls,
• Allows point and click control of face rotation (clockwise and anti-clockwise),
• Mouse cursor indicates current action of interest,
• Randomly scrambles cube,
• Can make permanent, or temporary rotations to any slice,
• On-screen control of perspective, scale, and position,
• Motions may be frozen, and restarted,
• A Fast/Rough and Slow/Smooth rotations are available for the cube slices,
• Animation may be turned off (cube face is rotated a full 90 degrees in one step),
• The user can edit all colors displayed,
• A complete user interface for the Ray Tracer parameters is provided.
2.4 Ray Tracer Features:
• Operates in batch mode,
• Models the Rubiks cube with a set of spheres,
• Uses a checkerboard floor under the cube (i.e., pattern mapping is used),
• A point light source is used,
• All optical coefficients of the objects may be changed,
• The ray depth is variable,
• Uses the same parameters used to view the Rubiks cube in the user interface (i.e., the images are almost identical),
• Image size is variable,
• The optical properties considered are,
i) Diffuse Reflection of ambient light,
ii) Diffuse Reflection of point light,
iii) Specular Reflection of point light,
iv) Reflection of light ray,
v) Refraction of light ray,
• Uses Phong shading.
2.5 Quantization Features:
• Will deal with an unlimited number of input colors,
• Outputs a colormap limited by 256 colors,
• Uses variable image sizes,
• File input/output formats are ASCII for portability,
• Fully automatic operation.
2.6 Display Features:
• Reads an ASCII file,
• Displays color file,
• Uses variable image sizes.
3.0 User Interface Review:
The user interface pictured in Figure 1 incorporates all of the functions described under the specifications. (See Appendix A for a copy of the first report). The screen is divided into two major sections, Control at the top and Display at the bottom. The controls are slightly different from the first report, but the operation is almost identical.
i) The mouse control options in the upper right hand side decide how cursor motions in the display window (with the left button depressed) will affect the view. This is a click and drag arrangement.
ii) The cube control options (also on the right hand side are almost the same as before, except the rotation may be set to coarser increments for faster rotation. Also, the erase of the cube before redrawing can be turned off, but this seems to have little effect on the speed.
iii) In the centre of the control window is the side selector. This will allow different sides to be selected. If the user points to select a face of the cube (described later) this menu will update to the last choice.
iv) The left hand side has basic buttons for the control of the cube. Most are identical to previous options, but in review, we will give a quick summary. The reset button will reset all viewing, cube and color parameters. It does not reset the ray tracing parameters. The scramble cube button will begin scrambling the cube and change to say “stop scramble”, hitting this button again will stop the scrambling. The two buttons for rotating the side are the same as before. The change colors button will bring up a color edit window. The edit view button will bring up a menu for directly altering viewing parameters. The ray tracing button will bring up the ray tracing settings window. There is the necessary quit button, and finally a freeze button. When the freeze button is pressed, it will suspend all animation on the screen. The button will also change to say continue. Pressing the button again will resume action.
Figure 1: The Main User Interface Window
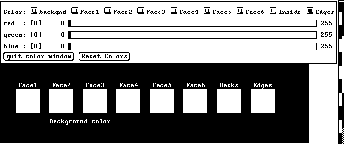
The color Window appears as in Figure 2. This window is essentially identical to the one presented in Appendix A. Basically the user will select the color of interest at the top of the window. The three sliders below will then show the color value for the item. The sliders may be used to alter the color. The bottom most window actually displays the colors. Two other buttons are available for quitting and resetting the colors. All color changes are made immediately.
Figure 2: The Color Edit Window
View parameters may be adjusted with the sliders shown in Figure 3 (this figure is incomplete) to alter any of the drawing parameters. The use of the sliders should result in immediate update of the display screen. The window may be dismissed with the view window off button.
Figure 3: The View Edit Window
Finally, the ray tracer window (in Figure 4) is used for generating the ray tracing parameter file. The use of the different variables will be explained later, but most variables are controlled via sliders. The only things not slider controlled are the revolving menus for image size and maximum number of rays. At the very top of the window is a button for saving the image to a file. The file name is specified in the line below. The extension ‘.scene’ will be added to the file name. There is also a quit button at the top of the screen.
Figure 4: Ray Tracer Parameter Window
3.1 General Notes:
The data structures described in the first report (Appendix A) are still used, and the discussion in that report is valid for almost all aspects of the graphics. There are two major revisions which supercede the previous report. These are the addition of an animation control structure, and the introduction of buffer swapping.
The buffer swapping was done by:
i) Swapping the screen with a memory block,
ii) Erasing the previous image (within a bounding box),
iii) Redrawing the image,
iv) Repeat the loop.
This gave smooth looking graphics without a redraw flicker. All utilities used were available through Sunview.
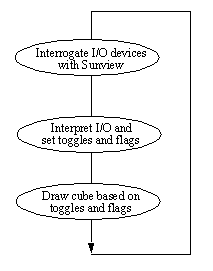
A sophisticated approach has been developed to permit the control loop to perform stop/start animation. This involves a two tiered approach. The first tier will examine inputs and user requests (from mouse and keyboard) which are then used to set and clear internal control flags. The second tier uses these control flags to decide how to redraw the object. During execution, the program loops through these operations, and thus provides a separation between simultaneous control, and display motion. As a result the user may start scrambling the cube, then look at it from different angles while the cube is rotating, and be able to freeze the motion at any time. With this architecture it is also easy to add more ‘real time’ control functions.
Figure 5: Basic Control Flow Structure
The use of hierarchical data definition and storage begins with abstraction of the sub cubes, from the cube data structure, and the cube data structure from the real world coordinate, and finally the real world coordinates from the transformed screen display. This hierarchy is also demonstrated by the ability to use the cube display to derive a data set to drive the Ray Tracer.
4.0 Ray Tracer:
The Ray tracer has a number of various features which are worthy of discussion. This section will attempt to cover each of the issues in enough depth to clarify the structure of the software. This section will begin first with a review of the models used. The section will then progress into discussion of advanced issues also to be handled within the software. The section will continue on to discuss the algorithms used.
4.1 Basic Ray Tracing Theory:
The theory of Ray tracing has two basic concerns. Firstly the light path is of interest, secondly the light transmitted is also of interest. These both involve interactions with real objects, thus light-object interaction must also be covered in this section. Note that in most models discussed the geometric relations are not given. Almost all of these relations are given, derived from other sources, or easily obtained with dot products.
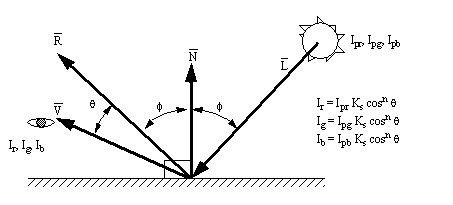
4.1.1 A Model for Diffuse Reflection of Ambient Light:
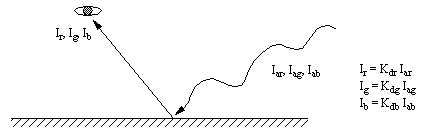
Ambient light is assumed to be evenly distributed over the entire volume of space. This naturally occurring light will provide a basic level of illumination for all objects.
Figure 6: Diffuse Ambient Lighting of A Surface
4.1.2 A Model for Diffuse Reflection of Point Light:
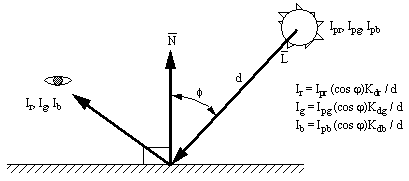
Point lighting is somewhat more sophisticated than Ambient lighting. In this case the direct light will illuminate the surface. The effect is approximated using the angle to the light source, and some constants (based on material properties) to estimate the ‘brightness’. Please note that this calculation is not done if the collision point lies in a shadow.
Figure 7: Diffuse Lighting of a Surface with a Point Light Source
4.1.3 A Model for Specular Reflection of Point Light:
The highlights which often appear on an illuminated object can be estimated also. In this case the Phong model is used. This model includes an estimate of how ‘fuzzy’ the light patch appears. This is not done if the collision point lies in a shadow.
Figure 8: Specular Reflection of Light
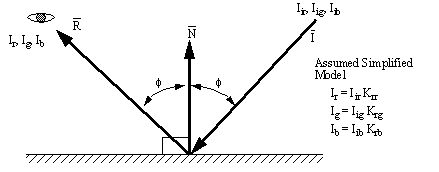
4.1.4 A Model for Light Ray Reflection:
When light strikes a surface it is often reflected. The reflection model is quite simple. In this case a simple fraction of the incoming light will be used. More sophisticated models may be constructed using information about particular materials.
Figure 9: Reflection of an Incident Light Beam
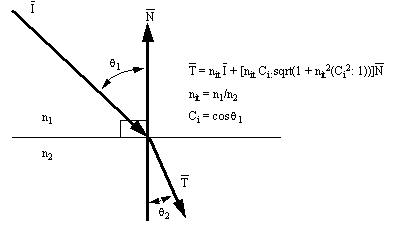
4.1.5 A Model for Light Ray Refraction:
When light enters or exits material, its path changes. There are also optical adjustments based on the transparency of the specific material. The path change is determined by Snell’s law, and the change in optical properties are considered by a simplified formula.
Figure 10: Refraction of an Incident Light Beam
After the collision vector has been calculated, the object’s transparency must be taken into account. This is done by using a transparency coefficient ‘t’. When ‘t’ has a value of 1 the object is opaque, and all light originates from the surface. If the object has a ‘t’ value of 0, then all light is from refraction.
Figure 11: Light Transmission in the Presence of Transparency
4.1.6 Collision of a Ray with a Sphere:
The method for finding the intersection between a ray and a sphere has been covered in “An Introduction to Ray Tracing” by Glassner [1989]. Therefore, the method will only be reviewed briefly. The method is quite simple because the relationship may be explained explicitly. To state the description in the book:
i) Find distance squared between ray origin and centre,
ii) Calculate ray distance which is closest to centre,
iii) Test if ray is outside and points away from sphere,
iv) Find square of half chord intersection distance,
v) Test if square is negative,
vi) Calculate intersection distance,
vii) Find intersection point,
viii) Calculate normal at point.
This algorithm gives at worst 16 additions, 13 multiples, 1 root, and 3 compares.
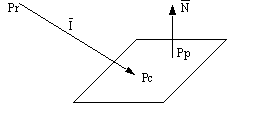
4.1.7 Collision of a Ray With a Plane:
A method for ray plane intersection was used to find collisions with the checkerboard. This method was devised from scratch. The proof will not be given, but it involves a parametric representation of the line, which is substituted into the plane equation. The parameter value was then found, and the collision point calculated. The algorithm for Line: Plane intersection is given below:
Figure 12: A Ray Colliding with a Plane
i) The dot product between I and N is found,
ii) If the dot product is greater than, or equal to, zero then the line does not intersect the plane,
iii) The line-plane intersection parameter is calculated (the dot product may be used here),
iv) The intersection point is calculated.
This algorithm is also based on an explicit relationship, therefore it is quite fast. In the best case there are 3 multiplies, 2 adds and 1 compare. In the worst case there are 12 multiplies, 1 divide, 10 adds/subtracts.
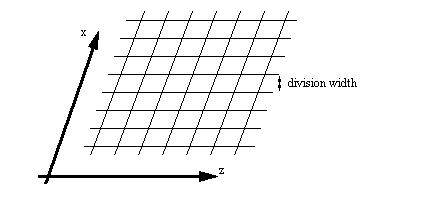
4.1.8 Mapping a Pattern Onto The CheckerBoard
This function was simplified by aligning the checkerboard along the x-z plane. This avoided the problem of having to transform the point on the plane (thus speeding calculations). The only problem to be considered was how to map alternating squares onto the floor. This involved a calculation of a remainder value when dividing the x-z location by the grid spacing.
.
Figure 13: A Surface with a CheckerBoard Pattern
The remainder function will find the offset from an integer number of divisions. This value will be up to plus/minus half a division. Thus,
4.2 Ray Tracer Algorithms:
This ray tracer will backtrack rays, and follow their paths through space. This involves a basic set of functions. First the general algorithm description is given for ray tracing, in general,
Figure 14: Basic Order of Higher Level Ray Tracer Features
This structure involves performing as many calculations as possible before execution begins. Although not all calculations are done before, some tricks will be described below which greatly improve the speed of ray tracing.
The process of filling up the image has multiple approaches. If a simple image is needed, then a simple scan of all the pixels can be made. An anti-aliasing technique requires oversampling of the pixels. When a pixel is chosen, the pixel must be mapped to a ray in space. This ray may be considered on a purely geometrical basis.
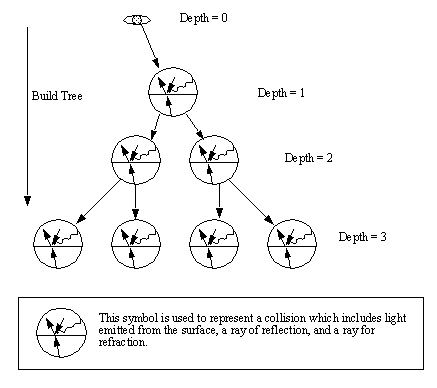
When backtracking rays in space, they will either hit an object, or take on the background color. If an object has been hit by a light ray, it can either reflect or refract, and it will take on the optical properties of the surface. This leads to a tree data structure for the collisions.
Figure 15: The Basic Concept of Back Tracing Rays
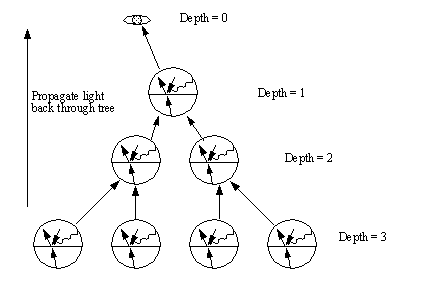
As seen in Figure 15, the light rays may be followed, but the only colors (color explanation follows later) attached to any nodes in this tree are the diffuse lighting from ambient and point sources, and also the specular reflection. After the tree has been fully expanded, the light may be traced forward to the eye. Figure 16 shows the light being propagated back up the tree to the eye (screen pixel).
Figure 16: The Basic Concept of Back Tracing Light Values in a Ray Tree
This structure gives rise to a tree based on a linked list. Each node in the linked list has:
Forward and back pointers,
Surface Normals, and optical properties for refraction (used for backtracking),
The lighting from diffuse and specular sources,
Vectors for before and after Reflection and Refraction,
Positions for ray origins and collision points,
The depth in the search tree,
The identification of which object the ray has come from and has hit.
All of these properties are used in a dynamic fashion, and the list may be grown until all branches have been terminate (i.e. hit background) or are at the maximum search depth.
This Ray tree structure is constructed with the data stored in a second structure. The second structure for scene data contains geometric information:
Objects for each ball including centres, radii, and ordered lists of the closest ball,
An object for the floor, eye, and light, including positions, orientations, and a list of balls, ordered from closest to farthest,
Transformation matrices,
he same perspective parameters used in the user interface,
list of picture areas only filled with background light,
Optical properties for balls, and floor: index of refraction, and shininess, transparency, diffuse, Phong, and specular constants,
The maximum ray tree depth,
Precalculated values for use in the program.
Both of these groups of data items have been ‘lumped’ together in separate data structures. As mentioned before the rays are organized as a linked list. The geometric information is stored in a second structure. By using this approach it makes it very easy to pass the various classes of information around the system, without pushing large numbers of variables on the stack.
4.3 Implementation Concerns:
There are a number of various implementation concerns. Most of these can be described as separate problems, which makes the implementation much simpler. Some interesting ideas arose in the development of efficiency improvement techniques. These were not only recalculation of values, but the pre-ordering, and pre-screening of processes.
4.3.1 Color Representation:
Colors were all represented with a normalized scale in the program. This approach allows continuous color representation to grow and decrease, and be scaled at the end of the image processing. One drawback to this is the cost on increased accuracy in calculations and has likewise lead to an increase in calculation time (i.e. doubles instead of ints). Before the unquantized image is saved to an ASCII file the colors are converted to a 0 to 255 scale. It was decided to clip all color values outside the 0 to 255 range. If afterwards it was found that the maximum color was less than 95% of the maximum, the colors were scaled to make the most use of the display capabilities. Note: the problem of color quantization is covered in the next section
4.3.2 Sorting Distances:
In an effort to speed computation, some tricks were devised, based on the geometry of the problem. In particular all of the balls were sorted by distance from an object. This was considered a good way to avoid checking all balls by ensuring that the closest balls are checked first. There are three cases of interest which are based on the object the light ray has come from:
Eye: The cube is assumed to be on the eye side of the floor, therefore the balls should all be checked first, starting from the closest and working towards the farthest. If no collisions have occurred, check for collisions with the floor, and quit if none found, the background has been hit.
Floor: The balls should be checked in order from closest to farthest, If none are hit, the background is hit.
A Ball: Each ball will have a list of its neighbors (closest to farthest) and each ball should be considered first, then the floor. If nothing is hit the color becomes the background.
The reader should note that the cases are based on a few geometrical properties. Firstly, if the balls are not touching the floor (and are visible) then any ray which hits them will not hit the floor. Also, because the balls do not overlap, they may be checked for collisions in order of depth. If one ball has a closer centre, it will never be overlapped by a ball further away. Thus, for each of the three cases listed above, all balls are sorted in order of depth from various targets, and when checking collisions, the above cases are applied (this seems to provide a great time efficiency by checking collisions in a random order).
4.3.3 Bounding Test Volumes
Bounding test volumes were set up, but these have proven to be ineffective in most cases where the scene is filled, their only benefit is in a nearly empty scene, where they save a ray calculation for every pixel. There are two main bounding volumes. The first volume is constructed around the set of balls. The second is constructed to represent the half of the screen which the floor will be displayed in (this could be all or none).
4.3.4 Shadows
Within the image there are certain objects which will be in shadows. In these cases there is a reduction in the amount of light. To detect this case a ray is traced between the light, and the point of interest (the only objects which will be hit here are spheres). If the light hits any spheres, the shadow is confirmed. When a shadow is confirmed, the specular reflection, and diffuse lighting from a point source are ignored.
To speed the checking process, the balls have been ordered by their distance from the light. The balls are checked in order, until one is hit, or the distance from the ball is greater than the distance between the point and the light.
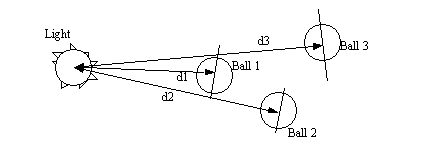
Figure 17: Depth Ordered Balls
In Figure 17 there are a set of balls ordered by depth from the light source. If we are looking for a shadow on any point of Ball 2, we first find a vector from the point to the light. The search then begins backward from the light. If the light strikes Ball 1, then Ball 2 is in its shadow. If the light misses it then Ball 2 is not in a shadow. Say we are finding a shadow on the floor, and the floor is known to be some distance (from the light) between Ball 1 (d1) and Ball 2 (d2). The algorithm would check for collisions with Balls 1 and 2. A check would reveal that the distance for d2 is greater than the distance to the floor, and since, no balls will have been hit, it may be concluded that the floor is not in a shadow, and the search is discontinued. This can save a great deal of search time when the light is close to the floor.
4.3.5 Aliasing:
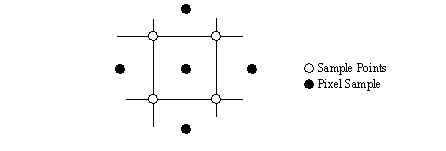
A problem with ray tracing is that features smaller than a pixel can be missed. Another problem is that features not aligned to the pixel grid become choppy. A method for solving this problem is Supersampling Anti-aliasing. This uses an approach where the pixel map is sampled normally, as well as between pixels, and the pixel values are combined.
Figure 18: Sample Points for Anti-aliasing
The black points in Figure 18 are sampled, the four points around it are used to adjust the value. This will tend to give a local averaging effect which overcomes sudden discontinuities in image space.
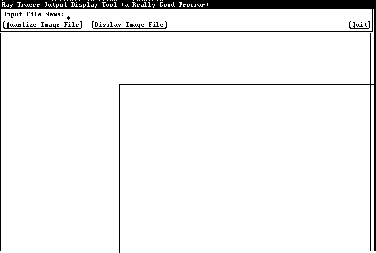
5.0 Display of Ray Tracer Image:
Figure 19: The Display Program Window
The display window shown below allows the user to enter the file name of an image to be displayed. If the file contains the raw image from the Ray Tracer, the user must first process it by selecting Quantize Image File. The color quantization program produces an ASCII file with raster format headings. If the image is stored as (an ASCII) raster file, the user may select Display Image File and display the image directly to the screen.
5.1 File Formats Used in Color Quantization
The input file to the quantizer is an ASCII file with information on the image produced by the ray tracer rendering module. The first two numbers represent the width and the height of the image. The remaining width*height entries represent the RGB intensities for each pixel in the image. An RGB vector representing each of these intensities is stored in the array, pict[]. The color vectors are used to set the colormap and to obtain the indices into the colormap for the image colors. The ASCII file used in processing the RGB values is portable.
The output raster file from the quantizer is also an ASCII file for portability. It contains raster file headers which is needed for reading the file by Sunview to display the image. The header information is as follows:
ras_magic = RAS_MAGIC 0x59a66a95 identifies file as a raster file
ras_width = x width of image in bytes
ras_height = y height of image in bytes
ras_depth = 8 number of bits per pixel
ras_length = x * y number of bytes in image
ras_type = RT_STANDARD = 1 standard raster file format
ras_maptype = RMT_EQUAL_RGB = 1 identifies colomap as RGB
ras_maplength = 3 * number of colors in colormap
Sunview expects the colormap to be stored with all the values for red intensities listed first, then the values for green, and then the values for blue.
The remaining values in the raster file are the indices into the colormap for each pixel in the image.
5.2 Input Raster File for Displaying the Ray Tracer Image
The output file from the quantizer is used as the input file for the ray display unit. As the raster header information is read, it is checked to verify that the input file is indeed a raster file and to determine its type, and the type of colormap used: in this case, RGB.
After the header information has been read and checked, the colormap is set up. Values for the red intensities are read in first, then the green, and the blue. The remaining information in the file holds the indices into the colormap for each pixel in the image.
Rather than using the binary read and write file commands, which are extremely fast, we have used the text file commands which are slower. The binary file is compact but unreadable, whereas the ASCII file is readable and portable.
6.0 Color Quantization:
The algorithm used for color quantization is the octree quantization method given in Graphic Gems by Andrew Glassner. In this method the RGB color information is read sequentially from an input data file. The first k different colors are used as initial entries to the color table. If another color is added so that there are now k+1 colors, some very closely related colors are merged into one and their mean is used as the entry in the colormap. This procedure is repeated for each additional color.
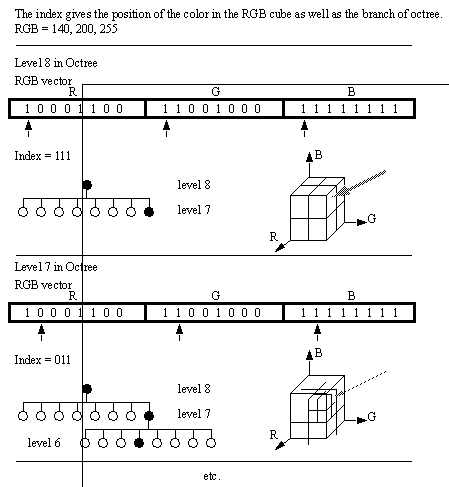
6.1 Representation of the RGB Cube
The RGB cube can be represented by an octree of depth eight by recursive subdivision of the RGB cube. The RGB values (0: 255) are coordinates into the RGB cube. The bit pattern, corresponding to the same level in the octree as the bit position, can be used as the index for the branch into the octree.
Figure 20: Mapping an RGB Value into the RGB Cube/Octree
6.2 Algorithm and Implementation
The algorithm has the following three phases:
6.2.1 Phase 1. Evaluation of Representative Colors
The first step to read the input data and insert colors into leaves of the octree.
InsertTree(Tree: Octree; RGB: Color);
begin
if Tree = NIL
then Make_and_Initialize_New_Node;
if Leaf
then
begin
{Update the number of represented pixels}
inc(Tree^.ColorCount);
{Sum the color values}
AddColors(Tree^.RGB,RGB)
end
else
InsertTree(Next[Branch(RGB)],RGB);
end
The next step is to combine successors of an intermediate node to one leaf node if there are more than the number of colors permitted in the colormap. Closest neighbors are found by putting the position of each leaf node in the octree into a linear list in sorted order and then finding leaves belonging to the same parent node. This is done by masking out the bits below a given parent node level and then finding a parent node with two or more children.
ReduceTree(Tree);
begin
{Find a reducible node}
GetReducible(Tree);
Sum := (0,0,0);
Children := 0;
for i : integer := 0,7 do
if Next[i] <> NIL
{There is an ith successor}
then
begin
Children := Children + 1;
AddColors(Sum,Tree^.Next[i],RGB);
end;
Tree^.Leaf := True;
{Cut the tree at this level}
Tree^.RGB := Sum;
{The node represents the sum of all color values of its children}
Size := Size: Children + 1;
end
6.2.2 Phase 2. Filling the color table
The k leaves of the octree contain the colors for the color table (RGB/Color Count). The colors are written to the table by recursively examining the octree and the index to the colormap is
stored in the node.
6.2.3Phase 3. Mapping the original colors onto the representatives
The image is read a second time using the RGB values stored in an array. For each color in the input, the representative color in the octree is found and its index to the color table is returned.
Quant(Tree: Octree; Original_Color: Color): index;
begin
if Leaf
then
return Tree^.ColorIndex
else
Quant(Tree^.Next[Branch(Orignial_Color)],Original_color);
end
6.3 Color Quantization Data Structures
The following structure for an octnode is the basic structure used for mapping RGB values into the octree:
structure octnode{
int leaf,
colorcnt,
colorindex,
level,
sumR,
sumG,
sumB;
struct octnode *next[8];
}
level is the level of the node in the octree,
leaf indicates whether the node is an interior node in the octree or a leaf node,
If the node is a leaf node,
colorcnt counts the number of input colors that have been mapped to the node,
sumR, sumG, and sumB are the sums of the color components of the colors that have been mapped to the node,
colorindex is the index assigned to the color in the node when the colormap is made.
Each node holds pointers to eight children. If the node is a leaf node, these pointers must be NULL pointers.
A list is used to hold octree positions for the representative colors in the colormap. The list is sorted in ascending order to facilitate finding the most closely related colors when it becomes necessary to reduce the number of colors to the maximum size allowed in the colormap.
list[256]
The colormap is a 3 by 256 array to hold the red, green, and blue color intensities.
colormap[3][256]
When colors are to be displayed, the color intensities for the pixels are obtained with an index into the colormap. The module which displays the ray tracer image also uses this data structure.
The RGB color vectors formed when reading the color intensities from the input file into the color quantizer are stored in an array:
pict[]
The color vectors are used initially as representative colors to establish the colormap and a second time to obtain the indices for the original colors.
7.0 Conclusion and Discussion:
This assignment was an excellent conclusion to the course. It allowed an opportunity to work with almost all of the major topics in the last half of the course, from shading to pattern mapping. As can be seen the ray tracer has been nicely blended into the software package, using external routines to make the entire package much more friendly.
Unfortunately the color nature of the images makes it impossible to include a high quality picture, but a few grey scale images have been included for the reader.
7.1 General issues
The entire package was produced in ‘C’. This was advantageous because of the tools available on the workstations for the graphics development. Sunview provided a number of tools for constructing high quality user interfaces. One drawback to Sunview is that under unix it cannot be allocated a time slice, therefore the animation may become choppy. Also, the slow nature of the processors hinders the speed of the ray tracer, although this is not a small problem.
7.2 Future Work
This work was done in a versatile manner that should allow easy extension to a more flexible ray tracer. As for the project itself, it is very good, but I suggest including polyhedra. These would add another interesting dimension to the image. The possibility of doing simple ray traced images with the same package is also exciting. Some other possible additions to the ray tracer could be,
Advance pattern and texture mapping,
Fog and lighting effects,
Multiple light sources,
Splines as primitives,
Estimates of non-point light sources,
New primitives,
Animation!
Trying optimization, or iterative numerical techniques on color quantization.
References:
7.1 Foley, J., Van Dam, A., “Fundamentals of Interactive Computer Graphics”, Addison Wesley, 1984.
7.2 Glassner, A.S., “An Introduction to Ray Tracing”, Academic Press, 1989.
7.3 Glassner, A.S., “Graphics Gems”, Academic Press, 1990.
7.4 Harrington, S., “Computer Graphics: A Programming Approach”, McGraw Hill, 1983.
7.5 Rogers, D.F., Adams, J.A., “Mathematical Elements for Computer Graphics”, McGraw Hill, 1990.
7.6 Wu, X., Course Notes for CS488/533 at the University of Western Ontario, 1991.
Appendix B: Program Listings
These will be made available by request.