Jack, H., “Backward Planning Based on a Boolean Equation”, University of Western Ontario, 1993.

Abstract:

Boolean representations can be used to describe physical models. In manufacturing these models must be interpreted into manufacturing operations. Computer Aided Process Planning (CAPP) systems are intended to map design features (geometry) into manufacturing features (operations/processes).

A planning system has been developed to examine Boolean equations, and select manufacturing operations. It does this by examining an equation for known patterns. A set of rules are used to alter the design equation and add steps to the process plan. As planning continues the equation is eventually reduced to a NULL state, at which time the process plan is complete.

This paper describes the planning approach, the rules, and the planning algorithms. A simple example is presented.

1.0 Introduction

Boolean equations are a very powerful form of representation. This representation is often used for the design of digital switching circuits and construction of solid models. While the equation will describe the final geometry or function of a design, it does not provide a process plan (a process plan directs the manufacture of the design), but, this representation can be used to derive a process plan.

We can think of manufacturing as starting with a product that does not exist. Well defined operations add and remove material to slowly transform a workpiece into a final product. At each stage we may stop and examine the part. And, at each stage this part will have a geometry that can be defined with a Boolean equation. If all of the operations from beginning to end are written in a list we would have a list with a NULL state at the top, and through incremental changes to the design equation we would arrive at the final, more complicated design equation. To take the concept one step further, if we look at the process plan in a tree form, we would see the root as the final design equation. Each arc would transform the equation, and add a sequence to the process plan. Each node would represent a design state, and the terminal nodes would be null equations. In addition the arcs leading from the nodes could be AND/OR in form. The AND branches would represent separate parts of the design that are produced separately, or are fully independent features on the design, and are both required. The OR branching is required because every manufacturing operation has alternates. A complete process plan would be the result of a complete subtree where there is a complete subtree with all nodes expanded, and a null term at the terminal leaves.

This form allows a planner to search design space [42]. A search begins at the root node where various equation components are undone or transformed. This leads to a number of AND/OR arcs. These are all kept, and based on cost estimates, one of the subnodes is expanded. This underlying search is best characterized as depth first. Each node is expanded to provide alternative operations in the case that a process plan step fails. The alternatives also provide the opportunity for backtracking when a dead-end is reached.

The planning algorithm also uses a number of other strategies, such as altering the form of the Boolean equation. Another paper in these proceedings describes tools for altering the structure of a Boolean equation [43]. This method has been successfully used to produce process plans for mechanical parts, as well as digital circuits [21].

It has been stated that Boolean algebra designs are prone to problems because of equation non-uniqueness [41]. This method begins to answer the problem of non-uniqueness by using it to seed the planning routine.

This paper will describe the reasoning system, and then conclude with a brief example that illustrates the method. The author intends to make the reasoning software available, as described in Appendix B. The paper begins with a discussion of process planning systems. Planning systems were used as the target for the work described in this paper, and serve as a good domain for exploring planning with Boolean equations.

1.1 Computer Aided Process Planning (CAPP)

Computer Aided Process Planning (CAPP) has had a number of distinct approaches. First, the Variant approach identifies standard part families to derive a set of standard process plans that are filed in a computer [11]. A classification scheme compares new parts with the standard parts to find the best match, the standard process plan for the standard part is recalled and changed to suit the new part [27]. This approach is suited to factories that have distinct part families, and when used has reduced the reinvention of similar process plans. This approach relies on human decision makers to select and update plans but does not use knowledge about process planning. Newer Generative CAPP systems attempted to bring knowledge of the factory into process planning. While this automates decision making, it requires a large scale effort to formalize the knowledge into a set of rules [27]. These systems may be dichotomized as: Variant systems store old plans, and Generative systems do not [8]. Importantly, both of these strategies are required for a planner that will be able to efficiently reuse successful plans when possible, but be able to generate required steps as required. To date there have been well over a hundred CAPP systems documented [1][9][13][16].

The notable successes for generative CAPP systems all limit planning to a specific manufacturing domain. For example, AUTAP [12] focuses on turned parts, CUTTECH [4] is a commercial system that generates process descriptions for machine operations, TOM [19] deals with holes, etc. All of these planners deal with the low level details of specific process domains, but what is required is a high level process representation that is not as closely tied to a specific manufacturing domain.

Modern CAD design systems use solid (geometric) modeling to create geometrical descriptions of parts. Generally the solid representation makes it possible to create a non-ambiguous model [18]. This has long been recognized in CAPP research as well. One of the earliest developments in the area [39] used feature recognition based on the relationship of solid primitives. This approach included a part design that was represented as an equation. More recent work continued with attempts to examine the Constructive Solid Geometry (CSG)/Boolean equations to recognize features [24][32][33]. Most of this work uses assumption of machined features extracted from base stock. One of the main criticisms of the use of CSG/Boolean equations is the non-uniqueness of the representation [40]. (NOTE: CSG representations use primitive shapes that are joined, or used to cut each other to form new shapes. These operations and primitives can be represented in tree or equation forms.) This non-uniqueness has two forms. First, the distribution of terms in the design tree/equation can vary. To overcome this, many authors have considered rearranging the representation as CSG trees or in equation form [10][14][20][21][23][24][28][34][35][37]. Second, non-uniqueness can result from different sets of defining primitives. To overcome this the approach would only examine the final geometry [36]. It has also been suggested that the equation primitives could be altered to generate the alternative geometries [20][21][23]. If the non-uniqueness problem of the solid CSG/Boolean method is to be overcome, a solid modeler will have to be incorporated to include geometrical reasoning [22]. Solid Modeling has many approaches. The most common types in use are CSG and Boundary Representation (B-Rep) (Note: B-Rep models the part faces and their interconnections). The B-Rep models can be derived from the CSG model, while the inverse operation is very difficult [6], thus CSG is a more general form. In fact most commercial modelers use the CSG operators (union, intersection and subtraction) to create B-Rep models [26][29]. As the CSG operators are used, the B-Rep model is constructed, and the operators are discarded. When these operators are kept they provide clues as to the construction of the specified part.

A solid modeler for manufacturing has special requirements. As mentioned before, the CSG information is often discarded, but it can be stored concurrently in a Hybrid modeler [17]. In addition the modeler must also consider non-homogenous materials [2][7][31], tolerance information [15], and attributes not directly related to geometry [3][5].

2.0 Undoing a Boolean Equation

The basic form of equations used in this planner are nested [43]. This means that brackets are used for each operator to explicitly define the scope. In addition each set in the equation, as well as terms, can have additional sets appended. These have been added to allow modifications to reused sets. In addition each of the sets mentioned refers to a list of properties. An example is given below

 

Figure 1: Various Algebraic Forms for Representing Designs

For the example above, the process plan can be found by looking at the final form. Each term will suggest a manufacturing operation. These possible operations can then be verified or eliminated by looking at the properties of the sets. If an operation is identified, it may be undone, and the new equation may be used for reasoning. This will continue until the plan is complete. The next section gives and example of this.

2.1 A Simple Example

Consider a design for a square part that has two tapped holes (internal thread), and is painted red. The design equation and sets are given below,

 

Figure 2: A Definition of the Part in Figure 1

Examining the equation in general, it would be recognized that ‘tapped_hole’ is a more complex part of the equation, therefore this would be a good place to begin planning. The ‘tapped_hole’ refers to a another equation twice, therefore the planner should reuse the results. At this point we will focus on planning for ‘tapped_hole’. The ‘EQUATION’ refers to a primitive type of set (in fact this is a feature based representation, not a geometry). Seeing that the operation is a ‘~’ NOT operation would lead us to question what is being removed. We would then compare the properties of ‘thread’ against known rule conditions. The only rule that would fire is for the internal thread. This would find that the form is a ‘3/4-10-UNC’ thread. The rule would then replace the sets, and modify the equation to replace the thread with a hole, suitable for tapping. The following form represents the modified components only,

 

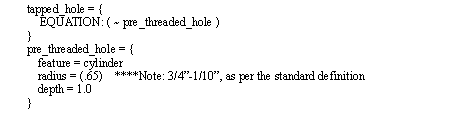
The same pattern as before would be used for this method, and it would be recognized that a cavity is still being cut from the base material. But, this time a rule would fire that recognizes that the hole can be drilled. This leads to the addition of a drilling operation to the process plan steps, and removal of the feature from the design representation. The resulting form would be,

 

At this point we would recognized that the equation is now somewhat irrational, containing NULL terms. Therefore the main equation will be examined, and it is found that two of the sets used ‘tapped_hole’ and thus refer to completed process plans. These would be added to the main process plan. These two steps would be modified by the addition of the appended sets. Both of the appended sets would specify rotations that would modify both of the ‘tapped_hole’ plans. At this point the design would be modified to compensate for the now completed, and removed tapped holes,

 

Now, we examine the equation, and find only a single term. This term is examined for other features. We recognize the color attribute as being significant, and decide to deal with it. To do this a painting operation is added to the process plan, and the paint set is deleted from the main equation. At this point the equation now looks like,

 

Looking at the equation we realize that all that is left is a small block of material. A cutting operation from stock is used to get the basic dimensions, and the stock is called from inventory. The square primitive is removed from the process plan, and equation reverts to a NULL, at this point planning is complete. A process plan for the completed part would be listed in reverse order from the order of planning, as is seen below,

 

While there was a fair quantity of ‘hand-waving’ in this example, the planning system basically performs tasks in the same manner. The following sections describe the mechanisms of the approach.

3.0 Finding Known Patterns in the Equation

When examining equations we tend to find common forms. These are part of a two step recognition process to identify possible rules. For example, we can look at the equation for ‘( & A B ....( ~ X )....’ and know that X is some form of geometry removed from ‘( & A B ...’. This is markedly different from ‘( + A B .... ( ~ X ) ...’ which could suggest that ‘( + A B ...’ be joined to everything outside ‘X’. It is not the intent of the author to classify these, but instead to provide tools to allow knowledge engineers to classify operations for specific domains. A list of common template elements are given below,

( X Start of a term, where ‘X’ is ‘?’ for any operator, or ‘+, &, :, ~’

for a specific operator.

) End of a term.

VAR:name:i Refers to a variable list of all sets within a term (not including sets).

VAR:name:x As above, but where the variable is ‘x’ position from the start.

(> This refers to the start of the expression only.

...( Allows a list of variables to be ignored before the start of a term.

...) Allows a list of variables to be ignored before the end of the term.

):LABEL:X Allow a variable ‘X’ name to be bound to a term.

):VAR:X Assigns all of the properties of a term to be given a variable name.

VAR:name:i:prop Same as above, but now it must have properties.

The list can be seen to deal with terms, operators, symbols, and appended symbols. When these are used in the rule set, they locate all possible matches, and then the variables in the template are matched to the variables in the equation. This allows rules to refer to sets in the equation.

An example of a template matched against an equation is,

 

The result of the comparison is that the template would match once, and for that case ‘V0 = D’. Say we had a more general template,

 

This template would result in three matches. In the first match we would catch the ‘&’ term and get the equalities ‘V0 = A, V1 = B, V2 = C’. The second match would be for the ‘~’ operator, and the equalities would be ‘V0 = D’. The final match would be for the ‘+’ operator, and the equalities would be ‘V0 = E, V1 = F’. The equation templates can be built up in this manner to get fairly complex forms of results.

It should be recognized that templates are quite rigid in the forms they will consider, but future work will examine a more flexible method, probably based on constraint propagation.

4.0 Condition Checking

After the templates above have been matched to the equation, they will then suggest rules that are possible matches. The rules have sets of logical conditions that must be satisfied, and actions that will result. Here we will examine the conditions.

The conditions for the rules are expressed in a Boolean equation (also reusing previous data structures) that will refer to the truth of conditions. Each condition has its own form. These are stored as a list of comparisons or operations that must all be satisfied concurrently for the condition to hold true. The conditions refer to variable names such as ‘V0’ from the template matching. A list of common condition statements/comparisons are,

COMPARE This instructs a comparison of the arguments. If the

comparison is false a false is returned.

MATH This performs a math operation. Obviously this is false if

the operation cannot be performed.

ASSIGN This will create a variable, and assign a value. There are

no cases at present that make this false.

FIND This will do a complicated lookup from a database or do

some geometrical calculations. This will also act as a catch-

all for all complicated algorithmic calculations. This will

be false if the required ‘FIND’ is not valid, or cannot be done.

The comparison elements are obvious in intent, but if any of the other operations fail, the condition is ruled negative. For example if the mathematical operation ‘PROERTY_FUNCTION_NUMBER ( DRILL_HOLE height / 20.0 )’ could not find the property ‘height’ in a set ‘DRILL_HOLE’, then the operation would fail, otherwise ‘height’ would take on the new divided result, and the line would be true in the condition.

5.0 Consequents

If a rule has matched, then the results (consequents) will be applied. This is basically a list of instructions that will alter the Boolean equation, add/change sets, and add lines to a process plan. A list of basic operators is given below that will alter the Boolean equation.

EQUATION_INSERT_SYMBOL

This will insert a symbol (a set name) at a specified position in an

active expression.

EQUATION_DELETE_SYMBOL

This function will delete a set name that is at a specified location.

EQUATION_DELETE_TERM

A term at a specified location will be deleted.

EQUATION_DELETE_VARIABLE_TERM

This will delete a term that has been given a label using the

‘LABEL’ operator in the template matching string.

EQUATION_INSERT_TERM

A given term will be inserted at the given position in the current

expression.

The operators that change the equation will affect a new copy of the equation. This is stored as a process planning state. In other words the changes that are made by the rule are for the new design state. Typical changes used are to eliminate terms, or replace them with updated sets. When referring to the location of terms, the rule acts as if the template matched term is the base, and from there the equation addressing scheme described is used.

Operators that affect the process plan, and general planning are,

PLAN_PUSH_TEXT

Adds a line of test to the process plan.

PLAN_PUSH_FORMAT

Adds a line of text to the process plan, but using a formatted

output. This allows the use of variables in plan output.

DECLARE_COST

A numerical cost is passed declared, so that the system may

perform some process selection based upon the cost of operations.

PROPERTY_FUNCTION_VARIABLE

Perform a math function based upon two variable names.

PROPERTY_FUNCTION_NUMBER

Perform a math function on a variable with a number.

FIND

This function allows complicated operations to be performed,

such as the lookup of the cost of a material, or a geometric

property. Many complex functions can be added through this

device.

Lines can be added to the process plan. In addition, the basic costs for the operation can be estimated. When used this will help reduce the search space with economic constraints.

Basic functions for manipulating the sets are,

COPY_SET

This simply copies one set to a new set.

ADD_SET

This function creates a new set.

ADD_PROPERTY

This function will add a property to a set.

PROPERTY_FUNCTION_VARIABLE

Performs a mathematical operation based on set members.

PROPERTY_FUNCTION_NUMBER

Performs a mathematical operation based on a set member, and a

number.

DELETE_PROPERTY

A specified property in a specified will be deleted.

The sets can be copied, and properties in them may be replaced/deleted/added, to the satisfaction of the new design state. In all cases, so that rules may be reused, each new set created is given a unique name (by appending a number) to prevent conflicts when it is used multiple times. This unique name is used in the design representation, but hidden from the rule.

6.0 The Planner

The planner basically works in two stages. First, the high level planner looks at the main equation, and finds all of the sub-terms, and possibly reused components. It then starts looking at the lowest level components, and tries to find process plans for them. In general terms the high level planner deals with the process plan tree. As each state in design space is to be expanded, the Low Level planner is used to match templates, and check rules. If the low level planner is not able to successfully expand a node, it informs the high level planner. The high level planner will try expanding the next lowest cost node. If the planner become frustrated, and cannot expand a node, it will try changing the form of the Boolean equation. This can seed the planner, and allow it to continue again. One significant note is that this only changes the equation, future work will examine changing the primitives that are used in the equation.

6.1 Low Level Planning

The Low level planner is pictured below.

 

Figure 3: The Low Level Planner

Here we see the basic steps of trying to find a matching equation template, checking the conditions of suggested rules, and performing the results if successful. The planner will continue until it has some minimum number of satisfactory solutions. If no solutions are found the planner becomes frustrated with that design state and returns to the high level planner.

6.2 High Level Planning

The high level planner is pictured below.

 

Figure 4: The High Level Planning Algorithm

The high level planner shown here utilizes backtracking, economy based search and rearranging the Boolean equation. The planner can also indicate when it is unable to plan for a design.

7.0 Conclusion

A planning system based on Boolean equations was described. It showed reasoning based on the form of the Boolean equation, followed by examination of the sets referred to in the Boolean equation. The effects of the application of the rules was also discussed.

The simple example provided shows the ability of the method to find process plans. Even more, the intuitive terms used to describe the process suggest that it models the human approach well (a commonly accepted intelligent system).

References

[1] Alting, L., and Zhang, H., “Computer Aided Process Planning: The State-of-the-Art Survey”, IIE Integrated Systems Conf. Proceedings, St. Louis, Missouri, 1988. Also appears in the International Journal of Production Research, Vol.27, 1989, pp. 533-85.

[2] Arbab, F., “Set Models and Boolean Operations for Solids and Assemblies”, IEEE Computer Graphics and Applications, November 1990, pp. 76-86.

[3] Arikan, M.A.S., and Totuk, O.H., “Design by Using Machining Operations”, Annals of the CIRP, Vol. 41, 1992, pp. 185-188.

[4] Barkocy, B. E., and Zdeblick, W.J., “A Knowledge-Based System for Machining Operation Processing”, Autofact 6 Conf. Proceedings, Anaheim, CA, 1984, pp. 2-11 to 2-25.

[5] Braid, I. C., “From Geometric to Product Modelling”, in Software for Discrete Manufacturing, editors J. P. Crestin, J. F. McWaters, Elsevier Science Publishers, 1986, pp. 123-133.

[6] Brun, J. M., “B-Rep to CSG Conversion as a Feature Recognition Process”, in Advanced Geometric Modelling for Engineering Applications, editors, F.-L. Krause, H. Jansen, International GI-IFIP Symposium 89, 1989, pp. 201-214.

[7] Casale, M.S., and Stanton, E.L., "An Overview of Analytic Solid Modeling", IEEE Computer Graphics and Applications, February 1985, pp. 45-56.

[8] Chang, T-C, Expert Process Planning for Manufacturing, Addison-Wesley Publishing Co., 1990.

[9] ElMaraghy, H.A., “Evolution and Future Perspectives of CAPP”, Keynote paper in the Annals of the CIRP, Vol. 42, No. 2, 1993.

[10] ElMaraghy, W.H., and Jack, H., "Facilitating Rapid Product Realization with an Intelligent CAPP System", Proceedings of IFIP Conference on World Class Manufacturing, Phoenix, Arizona, September, 1993.

[11] Emerson, C., and Ham, I., “An Automated Coding and Process Planning System Using a DEC PDP-10”, Computing and Industrial Engineering, Vol. 6, No. 2, 1982, pp. 159-168.

[12] Eversheim, W., Fuchs, H., and Zons, J.H., “Automatic Process Planning with Regard to Production by Application of the System AUTAP for Control Problems”, Proceedings of the 12th CIRP International Seminar on Manufacturing Systems, Belgrade, 1980.

[13] Eversheim, W., and Schulz, J.C., “Survey of Computer Aided Process Planning Systems”, Proc. of the 1st CIRP Workshop on CAPP, Vol.34, No. 2, 1985.

[14] Goldfeather, J., Hultquist, J.P.M., and Fuchs, H., “Fast Constructive Solid Geometry Display in the Pixel-Powers Graphics System”, Computer Graphics, Vol. 20, No. 4, Aug. 1986, pp. 107-116.

[15] Gupta, S., Turner, J.U., "Variational Solid Modeling for Tolerance Analysis", IEEE Computer Graphics and Applications, May 1993, pp. 64-74.

[16] Ham, I., and Lu, S., “New Developments of CAPP in U.S.A. and Japan”, CIRP Int’l Workshop on Computer Aided Process Planning, Hanover, FRG, 1989, pp. 1-23.

[17] Hardwick, M., and Spooner, D.L., "Comparison of Some Data Models for Engineering Objects", IEEE Computer Graphics and Applications, March 1987. pp. 56-66.

[18] Hoffman, C. M., Geometric & Solid Modeling, Morgan Kaufmann Publishers Inc., 1989.

[19] Iwata, K., and Sugimura, N., “A Knowledge Based Computer Aided Process Planning System for Machine Parts”, 16th CIRP Int’l Seminar on Manufacturing Systems, Tokyo, Japan, 1984, pp. 83-92.

[20] Jack, H., and ElMaraghy, W.H., "Computer Aided Process Planning With Boolean Algebra", CSME Forum-McGill University, Montreal, June 27-29, 1994.

[21] Jack, H., A Boolean Algebra Approach to High Level Process Planning, Ph.D. Thesis, at the University of Western Ontario, January 1994.

[22] Jared, G.E.M., Limage, M.G., Sherrin, I.J., and Swift, K.G., "Geometric reasoning and design for manufacture", Computer-Aided Design, Volume 26, Number 7, Jully 1994. pp. 528-536.

[23] Karinthi, R., and Nau, D., "Geometric Reasoning Using a Feature Algebra", in Artificial Intelligence Applications in Manufacturing, AAAI/The MIT Press, 1992. pp. 41-59.

[24] Lee, Y., and Jea, K., “A New CSG Tree Construction Algorithm for Feature Representation”, ASME Int’l Conf. on Computers in Engineering, San Francisco, CA, 1988, pp. 521-528.

[25] Mantyla, M., An Introduction to Solid Modeling, Computer Science Press, Rockville, Maryland, 1988.

[26] Miller, J.R., "Architectural Issues in Solid Modelers", IEEE Computer Graphics and Applications, September 1989, pp. 72-87.

[27] Nolen, J. Computer-Automated Process Planning for World-Class Manufacturing, Marcel Dekker Inc., New York, 1989.

[28] Okino, N., Kakazu, Y., and Kubo, H., “TIPS-1: Technical Information Processing System, for Computer-Aided Design, Drawing and Manufacturing”, in Computer Languages for Numerical Control, North-Holland, 1973, pp. 141-150.

[29] Requicha, A.A.G., and Rossignac, J.R., "Solid Modeling and Beyond", IEEE Computer Graphics and Applications, September 1992, pp. 31-44.

[30] Rivest, L., Fortin, C., and Morel, C., "Tolerancing a Solid Model with a Kinematic Formulation", Computer-Aided Design, Vol. 26, No. 6, June 1994, pp. 465-476.

[31] Rossignac, J.R., and Requicha, A.A.G., “Constructive Non-Regularized Geometry”, Computer-Aided Design, Vol.23, No. 1, February 1991, pp. 21-32.

[32] Ruf, T., and Jablonski, S., “Flexible and Reactive Integration of CIM Systems: A Feature-Based Approach”, CSME Mechanical Engineering Forum, Toronto, Ont., 1990, pp. 31-36.

[33] Sakurai, H., and Gossard, D.C., "Recognizing Shape Features in Solid Models", IEEE Computer Graphics and Applications, September 1990. pp. 22-32.

[34] Shapiro, V., and Vossler, D.L., “Construction and Optimization of CSG Representations”, Computer-Aided Design, Vol.23, No. 1, February 1991, pp. 5-20.

[35] Shpitalni, M, and Fischer, A., "separation of disconnected machining regions on the basis of a CSG model", Computer-Aided Design, Volume 26, Number 1, January 1994. pp. 47-58.

[36] Tang, K., and Woo, T., “Algorithmic Aspects of Alternating Sum of Volumes. Part 2: Nonconvergence and its Remedy”, Computer-Aided Design, Vol 23, No. 6, August 1991, pp. 435-443.

[37] Tilove, R.B., “A Null-Object Detection Algorithm for Constructive Solid Geometry”, Communications of the ACM, Vol. 27, No. 7, July 1984, pp. 684-694.

[38] Toriya, H., and Chiyokura, H., 3D CAD Principles and Applications, Springer-Verlag, Tokyo, 1991.

[39] Woo, T.C., “Computer Aided Recognition of Volumetric Designs”, in Advances in Computer-Aided Manufacture, edited by D. McPherson, North-Holland Publishing Co., 1977, pp. 121-1.

[40] Woodwark, J.R., “Some Speculations on Feature Recognition”, Computer-Aided Design, Vol.20, No. 4, May 1988, pp. 189-196.

[41] Yee, Y. C., and Fu, K. S., "Machine Understanding of CSG: Extraction and Unification of Manufacturing Features", IEEE Computer Graphics and Applications, January 1987, pp. 20-32.

[42] Korf, R.E., “Planning as Search: A Quantitative Approach”, Artificial Intelligence, 1987, pp. 65-88.

[43] Jack, H., “NB: A Library for Storage and Manipulation of Nested Boolean Equations”, to be presented at Solid Modelling ‘95, Salt Lake City, Utah, 1995

Appendix A: A Sample of a Rule File

This is a sample taken from a complete rule file. Only selected sections have been taken to reduce space usage, but there are enough sections here to perform a drilling operation.

equation_form EQN_1 {

EQUATION: ( & ...( ~ VAR:V:0 ):LABEL:REF

RULE: drill_hole

RULE: chamfer_drill

}

equation_form EQN_9 {

EQUATION: (> : VAR:V:0 VAR:V:1 ...)

RULE: assemble_parts

}

rule assemble_parts {

EQUATION: ( & PART_0_EXISTS PART_1_EXISTS )

RESULT: ASSEMBLE_PARTS

}

rule drill_hole {

EQUATION: ( & CYLINDER_SHAPE DRILL_SIZE )

RESULT: DRILL_HOLE

}

rule chamfer_drill {

EQUATION: ( & CONE_SHAPE DRILL_SIZE )

RESULT: DRILL_CHAMFER

}

condition PART_0_EXISTS {

COMPARE ( V0.form $ )

}

condition PART_1_EXISTS {

COMPARE ( V1.form $ )

}

condition CYLINDER_SHAPE {

COMPARE ( V0.form == CYLINDER )

}

condition CONE_SHAPE {

COMPARE ( V0.form == CONE )

}

condition DRILL_SIZE {

MATH ( V0.ratio = V0.height / V0.radius )

ASSIGN ( V0.minimum = 0.5 )

COMPARE ( V0.ratio > V0.minimum )

COMPARE ( V0.ratio < 20 )

COMPARE ( V0.radius > 0.05 )

COMPARE ( V0.radius < 2.5 )

COMPARE ( V0.height > 0.1 )

COMPARE ( V0.height < 15.0 )

}

result DRILL_HOLE {

EQUATION_DELETE_VARIABLE_TERM ( REF )

ADD_SET ( DRILL_HOLE )

ADD_PROPERTY ( DRILL_HOLE a1 = 0.5 )

ADD_PROPERTY ( DRILL_HOLE a2 = 1.0 )

ADD_PROPERTY ( DRILL_HOLE height = 0.0 )

PROPERTY_FUNCTION_VARIABLE ( DRILL_HOLE height + V0 height )

PROPERTY_FUNCTION_NUMBER ( DRILL_HOLE height / 20.0 )

FIND ( DRILL_HOLE name SET_NAME V0 )

PLAN_PUSH_FORMAT ( ‘ DESCRIPTION ( drill hole : ‘

DRILL_HOLE.name ‘ ) ‘ )

DELETE_PROPERTY ( DRILL_HOLE name )

PLAN_PUSH_TEXT ( ‘ CUTTING ( FEATURE single diameter hole ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( MACHINE qa1000 ) ‘ )

PLAN_PUSH_TEXT ( ‘ CUTTING ( MATERIAL t-7075 ) ‘ )

PLAN_PUSH_FORMAT ( ‘ CUTTING ( PARAMETERS ‘ DRILL_HOLE.height

DRILL_HOLE.a1 DRILL_HOLE.a2 ‘ ) ‘ )

// A costing section is added here for a trial run

ADD_PROPERTY ( DRILL_HOLE cost = 0.0 )

PROPERTY_FUNCTION_VARIABLE ( DRILL_HOLE cost + V0 height )

PROPERTY_FUNCTION_VARIABLE ( DRILL_HOLE cost * V0 radius )

PROPERTY_FUNCTION_NUMBER ( DRILL_HOLE cost * 1250.25 )

PROPERTY_FUNCTION_NUMBER ( DRILL_HOLE cost + 0.25 )

DECLARE_COST ( DRILL_HOLE cost )

}

Appendix B: Getting the Software

An ftp site is being set up, and should be available by early 1995. The basic procedure is to ftp to cobra.megan.ryerson.ca, and look in the directory ‘/pub/software/tools/BCAPP’. The contents will be a copy of this paper, as well as more complete function descriptions, examples, and the source code. If the software is desired before this time please send email to ‘hjack@megan.ryerson.ca’.