2. The Controller
The controller the students analyze and build is based upon a transistor which switches power to the motor. To allow the effective voltage to be varied, a pulse width modulation method is used, as shown in Figure 1. The power is switched fast enough so that the dynamic effects of the motor filter out the effects of the rapid switching. Typically this can be a frequency as low as 100Hz, although a higher frequency is better, and above 20KHz puts it above the audible range. This method does require some sophistication to generate the PWM signal, but the result is a much simpler and more efficient power amplifier.
Figure 1: PWM (Pulse Width Modulation)
The motor control system is connected as shown in Figure 2. The counter output from the computer drives a TIP-120 (Darlington coupled NPN) transistor that switches the voltage from a high current (>1amp) voltage supply. When the counter output is on (+5V) the transistor turns on and allows current to flow. In this configuration the voltage across the transistor is about Vce = 2V (the Vce value is available in the transistor datasheets). This means the maximum voltage delivered to the motor is Vs = Vp: Vce. Multiplying this by the duty cycle gives the effective (RMS) voltage delivered to the motor. The shaft of the motor is coupled to the tachometer. The tachometer can be any permanent magnet DC motor. When the shaft of the motor is turned, it acts as a generator and delivers a voltage that is proportional to angular velocity. The voltage from the tachometer is read as an analog input (Vt) to the computer.
Figure 2: The schematic for the DC motor controller
Part of the setup procedure requires that the speed-voltage ratio for the tachometer be established experimentally. This is done by supplying a voltage to the motor, and measuring the motor speed (ω) and tachometer voltage (Vt). We normally measure the angular velocity with a strobe light tachometer. Multiple readings are taken by changing the motor voltage and then repeating the previous readings. Graphing the data should yield a straight line and show a linear relationship. The data can be used to determine the coefficient ‘Kt’ in the equation Vt = Kt(ω).
The computer is interfaced to the process through a National Instruments PCI-1200 DAQ card [3]. It is used to read the analog voltage input from the tachometer and generate the PWM motor output with a counter. The PWM output is characterized with a frequency for the output pulses, and a delay for the on/off transition as shown in equation 1. In this application the frequency remains fixed, but the counter value is changed to vary the duty cycle. When using the counter the upper and lower limits must not be exceeded. At best this will make the system non-linear, at worst it may make the motor output unpredictable.
A Labview program, similar to that shown in Figures 3 and 4 is written by the students to handle inputs and outputs, and do calculations. The front panel is shown in Figure 3. It has a knob so that a desired speed can be set, and a chart that displays the tachometer speed reading as a function of time.
Figure 3: Labview front panel for the control system
The wiring diagram in Figure 4 shows the basic system setup. Variables have been labeled so that they correspond to the equations in this paper. Outside the while loop there is a calculation that only needs to be done once, and the “PULSE CONFIG” function to setup the counter on the PCI-1200 DAQ board. Inside the while loop are the functions that should be repeated each scan. On the left hand side the analog voltage is read in using the “AI ONE PT” function block. The voltage is converted to a speed and subtracted from the desired voltage. It is then multiplied by the controller gain constant to obtain the desired motor voltage. This is then converted to a counter value that will produce a corresponding PWM output with the “ICTR Control” function block. This program does not include functions to limit the values to the counter. The scan time is notably absent in this program because the proportional control equation is not a function of time.
Figure 4: Labview wiring diagram for the proportional feedback controller
The equations for the control system are given below. Equation 2 was obtained by manipulating equation 1 to isolate the desired value for the counter as a function of the desired motor voltage. Equation 3 is the proportional feedback controller. Equation 4 is the speed-voltage relationship for the tachometer. Equation 5 is a simplified differential equation for a permanent magnet brushed DC motor, relating the speed of the motor to the supplied voltage. In the equation the ‘K’ and ‘R’ values are fixed, but the ‘J’ value is a function of the inertia in the system. This equation obviously ignores friction and viscosity effects.
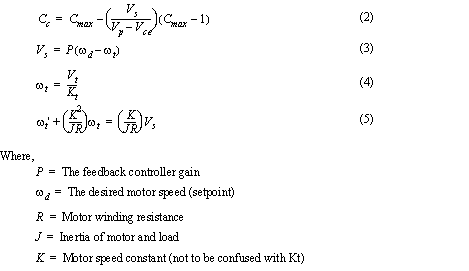
The coefficients for the motor equation can be found using the method shown in Figure 5, although other methods are available. In this case the resistance of the motor windings is measured directly. The motor speed constant and the second moment of inertia are determined by applying a voltage step input to the motor and observing the first order response. The steady state speed is used to determine the motor speed constant. The second moment of inertia is determined by finding the time constant of the response and relating it to the coefficient in the first order differential equation for the motor. This method is not perfect, but from a pedagogical perspective it strongly reinforces many important principles of first order differential equations.
Figure 5: A sample calculation for determining motor constants experimentally
Once armed with the constant values for the motor and the tachometer, the system response can be modeled theoretically. The equations for the feedback controller and the motor can be combined and simplified to obtain equation 6.
Please note that the solution shown uses an abbreviated method. Other methods may also be used, but will result in an equivalent solution.
The laboratories were structured to distribute the laboratory over a three laboratory sequence, as listed below. In the first week students connect a simple motor controller. This establishes a level of comfort with the concepts of pulse width modulation and using transistors for power switching. The second week builds upon the first including the use of motors as tachometers and motor modeling. The third week integrates the components into a feedback control system.
Lab 1: PWM Control Tutorial: Students are shown how to develop a Labview program to use a DAQ card counter to generate a PWM output from the computer. They then connect this through a transistor to control the speed of a motor.
Lab 2: Motor Modelling: The constants for a motor are calculated using the technique described earlier. Students are introduced to using a motor as a tachometer.
Lab 3: Feedback Control: The full feedback system is built and tested. The results are compared to theory.
The results of the experiments are documented in formal laboratory reports. In addition to expected elements, these ultimately include a comparison between theoretical and actual responses of the feedback systems. Through this lab students find the common problem with the proportional controller, particularly the significant steady state error. This supports the lectures by providing a basis for discussion of the Integral and Derivative components of a PID controller.