• A model is used to mathematically capture some aspect of the real world so that it may be manipulated, studied, tested, etc.
• To computerize a design we will capture a very explicit model of a part in a computer program.
• Geometry is by far, the most important part of any design. It is used as a reference for tolerances, processes, functions, materials, assemblies, etc.

• Three major functions in geometric modeling,
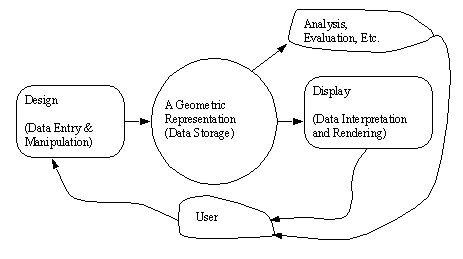
• The Geometric Representation determines what a system can do.
• There are a number of methods of representing geometry, 1D, 2D, 2.5D, 3D
2D: All in one dimension, such as a side view of a part
2.5D: Points have an x, y coordinate, and height. This is a special case which can describe raised surfaces like buildings.
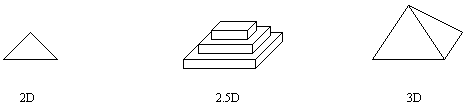
• 2D models are quickly becoming obsolete, 2.5D models were an early compromise, but 3D models are quickly becoming the standard.
• There are many ways to model a part, the major categories are,
Elemental (using lines and points like drafting)
Surfaces (such as polygons used in ES 206)
• If describing a block with a hole in it, each of the methods above will result in different descriptions


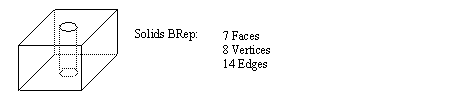
• Which is best???? all of them in the right situations.
• Each method has its particular advantages, and disadvantages.
• The best software and hardware supports a combination of all methods.
• It is assumed that other information is used to describe the geometries above, like,
• The geometries can also be used to associate other information,
• Depicted with the simplest of details (lines, points arcs, etc.)
well suited to line based problems
does not require a powerful computer
easy to perform traditional drafting
not capable of carrying complex information
complex items require long time to model
very hard to connect to programs for FEM, etc.
• Typically used in older CAD systems like AUTOCAD, CADKEY, etc.
• A classic demonstration of the arbitrary nature is shown below,

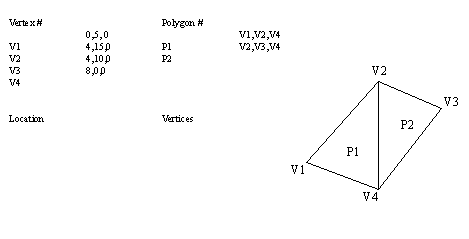
• The geometry is described with polygons which should represent an entire surface of an object.
• Generally these polygons do not indicate which side a volume lies on, but inside/outside is defined with tricks like defining polygon vertexes so that counter-clockwise is out.
• STL is a good example of an engineering use of this surface representation.
• This method is also used in computer games where speed is important, and the overhead of the full solid information is not desired.
well known, and fast software and hardware for drawing.
because objects are not solid, they may be subject to ambiguities
hard to pass data to other systems, like FEA
polygon selection is problematic
• Commonly used in graphics packages like HOOPS, PHIGS, CORE, etc. Also acts as the basis for the SGI computer graphics.
• An example of the polygon meshes is given below.
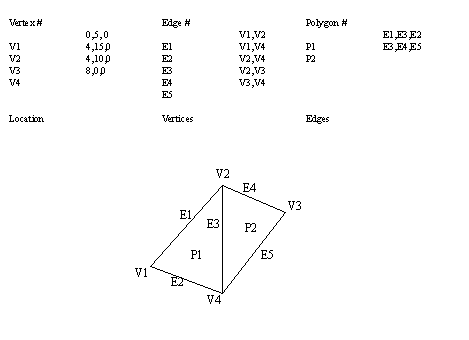
• We can also define these geometries using edge meshes.
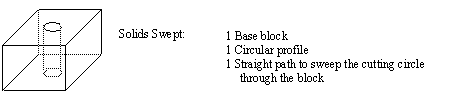
• A profile is created in 2D, and then swept along a path to create a volume, or to cut a volume.
• The path may be straight, rotating about an axis, rotation along a helix, following a curved twisting path.
Can make very complex parts quickly
• This still bears a remote resemblance to Surface Modeling.
inside/outside is defined for each surface
the edges, and vertices of touching faces are defined
can store very complex geometries
easy to propagate changes to faces, edges and vertices
can easily generate and store complex surfaces
many systems support this method, such as PARASOLIDS, ACIS, etc.
high Level information is still not present in model
hard to recognize some simple features like a block
• A BRep object is pictured below,
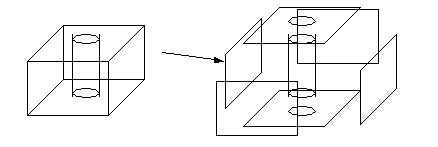
• Each feature in a B-Rep object can be varied independently
• Geometry is kept in parallel with the object topology. One example of a data structure is seen below.
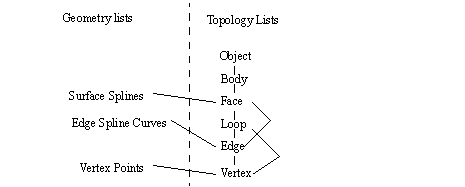
• A common data focus uses the edges of an object to define the shape (vertices and faces can also be used)
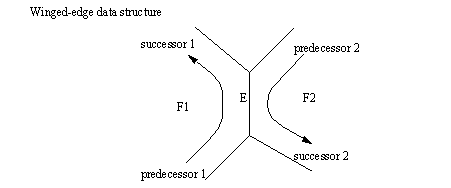
• Euler operations can be used to build an object.
• We can check to see if the solid model is valid using the basic Euler equation, or the more involved Euler-Poincare topological equation. These equations must be satisfied for the models to be valid.

• When developing solid modelers we can use the Euler operations to ensure that the model stays topographically valid at all times.
• Does not calculate lines/vertices/faces when storing part geometries
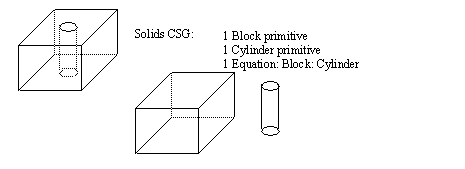
• Uses primitive shapes such as planes, blocks, spheres, cylinders, wedges, torii, etc. to model shapes
• The primitives can be rescaled to meet requirements
• Uses a basic set of operators to combine or cut with the primitives,
Union: Both primitives are joined into one (boolean OR)
Intersection: The part of the primitives which overlaps (boolean AND)
Assemble: Parts may overlap without being joined
Difference: The area of one primitive is removed from another
• Basic common primitives are,
Primitive shapes match human though processes
Very fast when creating parts with standard geometrical features
Slow because all interpretation is done at once
may be difficult to incorporate irregular surfaces
• Used in systems like PADL2, Romulus, Build, etc.
• CSG designs can be stored in trees
• Various types of CSG operators are possible based on closure of sets. In particular we can consider two boxes that touch, but don’t overlap.
• Halfspaces can be used for defining boundaries of an object.
• Space is broken down as a regular/irregular grid.
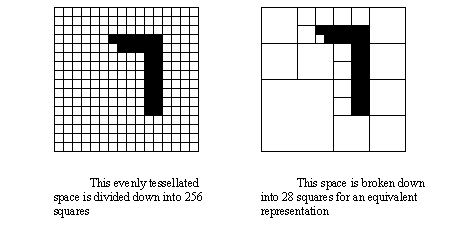
• locations in space are marked as occupied/empty/partially filled.
• this method is most common when using scanners such as CAT and MRI that collect data in voxels (these are small rectangular volumes)
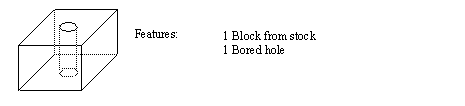
• The designer would simply define a part in terms of fundamental manufacturing features, such as chamfers, through slots, blind slots, etc.
• Very high level, but can complicate additions of unanticipated features, like a ridge in a car hood.
very intuitive and easy to use
can simplify other aspects of CIM (eg. If a standard feature is used there will be a standard process plan to make that feature).
emphasizes the use of standard components.
restrictive when dealing with nonstandard features
interaction of features can be hard to estimate
a complete set of all possible features would be very large
• There are two levels of features commonly used in these systems,
• A set of standard features for rotational parts might be,
• A Numerical integration may be done on the geometry of a part by examining its components. From this mass, Polar and Cartesian moments of inertia, and centre of mass may be determined.
• An approximate division of space is often used called oct-trees. In this case the volume of the object is recursively broken down into finite parts. Other methods use an even division of space.

• Is most successful with solids models.
• A manifold part makes sense mathematically. A non-manifold part may be interpreted in a number of ways, when dealing with general cases.
• Some examples below show manifold/non-manifold shapes

vertices with less than 3 adjoining faces
edges with more or less than two adjoining faces
• Non-manifold parts are required for,
composite material modeling in a single part
assembly modeling where parts touch or overlap (press fit)
other Future Applications ????
• Many CAD systems experience numerical problems based upon the nature of floating point arithmetic.
• This can result in points, and surfaces being distorted, and this may cause errors during comparison.
• To overcome the problem, most systems will allow a “point tolerance” value to be used to numerically compare, and join separated point.

Problem 16.1 Discuss the statement “Line trimming can be essential when constructing solid models”.
Problem 16.2 a) For the part below, describe how it would be represented with a winged edge B-Rep data structure. Draw the winged edges, then create data arrays.

b) For the model in part a) suggest how tolerances could be added to the arrays.
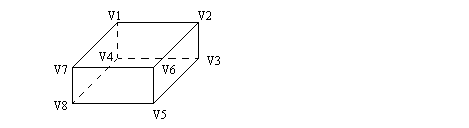
Problem 16.3 Draw a B-rep solid model representation for the box below. Vertices have been drawn, you will need to add the other data elements to complete the model.