3. EGR 345 - Dynamic Systems Modeling and Control - Older Laboratories

3.1 Laboratory Writing Assignment

• Background: Laboratory work is something that all engineers need to ensure that theoretical estimations match practical reality. In a factory, the "laboratory" might be the a machine where tests are conducted and the metrology room where final dimensions are checked. When doing experiments there are some critical components i) clear purpose and expectations, ii) good methodology and iii) thorough analysis and reporting of the results. In school students learn to formulate questions, and when working these will arise naturally, satisfying step i). Step ii) is practiced in school and this will develop over time. Step iii) requires the most maturity and effort. A high quality analysis and report of results will often sway million dollar decisions.

• Objective: To extend a standard laboratory report so the writing and theory are now presented at a professional level. This should be at the level of a report generated by a consultant.

• Subject: The laboratory to be analyzed will be announced in class.

• Audience: The level of the writing should allow one of your fellow students to read it with all the knowledge they have. Avoid being didactic: don’t try to lecture them.

• Required Sections: The report should be approximately 2000: 3000 words, and include equations, figures, tables, graphs and other exhibits, as required. All of the contents should be prepared as indicated in the course note set on writing. The report structure will have the main section headings below, but may also have subsections.

Executive Summary/Abstract: A brief overview that describes the contents of the report and the results. This should include numerical results and accuracies.

Introduction: A section that prepares the reader with relevant information to read the rest of the report.

Theoretical Models: This section should detail the relevant theory to predict system behavior.

Experimental Methods and Results: This section should describe the experimental equipment, how it was used to make measurements, and the data measured. For this report do not use numbered procedure steps.

Analysis and Discussion: This section should compare the accuracy of the theoretical models to the experimental data collected. Numerical comparison of values is expected.

Conclusions: This section will briefly review the important points of the report. This is a good place to make statements about the results (refer to numbers), but avoid statements such as "this was a wonderful experience".

• Tentative Schedule (This may change):

September 20th: the normal lab is conducted and a standard lab report is submitted.

September 27th: the graded reports are returned, and work on the full report begins.

October 10th: the first draft of the full report is due.

October 17th: the graded reports are returned.

November 4th: the deadline for the final draft.

November 8/10th: oral presentation during lab time.

• Marking of the final report will be done with a form that looks something like the one below,

 

3.2 A Special Project

• Background: Many of us recognize that the internet does not have enough quality content. To help raise the overall standard of information on the net, we should create some content in the form that would be most useful to us.

• Objective: To create a multipart document that discusses technical topics in detail.

• Method: To make the document more complete, the work will be split into topics. Each student will research and write a chapter on a different topic. These will be tied together through a common table of contents. Each chapter will be self complete. The files will be completely in HTML so that anybody else will be able to view the final results.

• The Audience: The intended reader will be other engineering students looking for information on various topics. The chapters will include equations, figures, tables, graphs, etc. as required. This might be viewed as similar to a technical encyclopedia.

• Possible topics might include,

dampers

coil springs

op-amps

filters

belts

chains

nuts/bolts

ball joints

valves

hydraulic cylinders

vacuum pumps

fluid pumps

pin joints

sliders

cables

pulleys

aerodynamic drag

pressure hoses

common hydraulic fittings

common pneumatic fittings

gears

latches

flanges

brackets

elastomers

3.3 Lab 3b: Estimation of Capacitor Values

• Objective: To estimate the value of a capacitor using measured values.

• Theory:

 

 

• Prelab:

1. Read the theory section, and set up a Mathcad document to calculate capacitance using measured voltages and times.

• Procedure

1. Set up the circuit shown in the theory section using R=1M, C=100uF. Put in a switch so that you can add/remove a voltage (hence we can get a d/dt V). Use a computer with LabVIEW to measure values needed to find the needed values. Use Mathcad to calculate the capacitor value.

• Post-lab:

None.

• Submit:

1. The Mathcad document used to estimate capacitor values, and the final estimate.

2. A summary discussion of the lab results.

3.3.0.1 - Lab 4b: Electrical Components

• Objective:

This lab will study a simple electrical system consisting of resistors and a capacitor using instrumentation and Labview.

• Theory:

Recall the basic circuit equations for electrical systems.

 

 

• Prelab:

1. Determine a method to find the value of an inductor.

2. Create Mathcad sheets to support calculation of capacitor and inductor values.

• Procedure

1. Measure the values of the resistors.

2. Find the value of the supplied capacitor using a computer running LabVIEW.

• Post-lab:

1. Compare the estimated values of the components to those found on the device labels.

• Submit:

1. Mathcad sheets prepared in the prelab.

2. Estimated values of the capacitors and inductors.

3. A laboratory report posted to the web.

• Objective:

To review methods for technical writing.

• Theory:

Before starting to write you need to make some clear decisions. These include,

Who are you writing for? Who is your audience?

What does the reader want to know?

What is the objective for the written work?

After answering these basic questions you can plan the layout for the paper.

What are the general divisions for the topics?

Is there a conventional forum for the topics?

What is a logical flow for the work?

What can you tell the reader that they need to know?

What is a reasonable depth or level for the writing?

At this point personal styles will drive writing techniques. For technical work it’s best to follow this general sequence:

1. Determine major questions that need to be researched (lay out what you know in point form)

2. Do research as required (add point form notes and add references for things that aren’t obvious, or may be useful to others interested in the area. It is very helpful to add equations and figures at this point.

3. Review, rearrange, and edit the point form notes. Check to see that they match your writing objectives.

4. Group and divide the notes into sections. Check to see if the sections flow.

5. Go through and convert the point form to sentences, etc.

6. Proof read and fix obvious problems.

7. Give to somebody else to proofread. It is best to use a technical reader.

8. Proof read again, and then format.

9. Skim to check that the general appearance is good.

• Prelab:

1. Develop an idea(s) for a research report that is related to the modeling or control of dynamic systems. Your instructor may assign an idea or topic to you.

2. Answer the questions in the theory section in the context of your idea(s) for a research report.

• Procedure:

1. The lab will begin with a discussion of writing skills and writing techniques.

2. The pre-lab ideas will be developed into point form notes.

3. Research areas will be identified.

• Post-lab:

1. Develop a brief synopsis that is one page or less that outlines the paper topic and approach. Also note major problems that must be overcome.

• Submit:

1. The prelab work.

2. The synopsis.

3.4 Lab 6b: Resonant Oscillations in Electrical Systems

• Objective:

To study frequency response in resonant electrical systems.

• Theory:

In mechanical systems we typically get oscillations with masses and springs at their resonant frequencies. These components are similar to capacitors and inductors in electrical circuits since they all can store energy. There are two common types of resonant electrical systems: series and parallel LC pairs.

 

Finding differential equations that relate the input to output voltages (across the resistor) will result in second order differential equations.

• Prelab:

1. Develop the differential equations for the two circuits above.

2. Use Mathcad to estimate the response of each circuit using a numerical method. Use the circuit component values given below.

• Procedure

1. Review the tutorial for reading scope data into LabVIEW.

2. Set up the series LC circuit with the values R=10K (?), C=1uF, L=1uH.

3. Connect a signal generator to the input, this will also be connected to LabVIEW.

4. Use the vi program provided to sweep the sinusoidal frequency of the signal generator. Record the input and output magnitudes. Ensure that the values show the transition region in adequate detail.

5. Repeat the process for the parallel LC circuit.

• Post-lab:

1. Graph values of the gain of the two circuits using Bode plots in Mathcad.

2. Compare the theoretical and experimental responses.

• Submit:

1. Submit all work by posting to a web page.

3.5 Lab 7a: Magnetic Damping (Button Magnet Drop)

Caution: Neodymium magnets used in the lab are small but their magnetic fields are very strong. Keep them away from disks, electronics, etc. Also take care when handling more than one of these magnets, they will pinch skin, or come together quickly and chip.

• Objective:

To observe damping in a complex system.

• Theory:

As we move a continuous mass of metal into a steady (static: non-time varying) magnetic field, an electric current (due to electron flow) will be induced in the metal. If we move faster, then the current will be greater, but the motion will be over faster, resulting in the same net energy. If there is no place for charges to flow, then there won’t be a current (infinite resistance). But, when there is a path for the current to flow the current flowing in the metal sets up an opposing magnetic field and an opposing force (low resistance). If we could find a perfect superconductor (zero resistance) the force would approach infinity.

You can see a simple example of this effect by trying to turn a DC motor shaft with the wires disconnected (easy to turn), and then shorted together (hard to turn). This phenomenon only occurs when the fields are changing. The electron flow in the metal is typically referred to as eddy current, and is a huge problem in actual devices, such as transformers. This is why transformers get hot and are only about 98-99% efficient.

We started with the idea of moving metal in a magnetic field. But, if we keep the metal still and move the magnet we can get a similar effect. In this lab we will drop a magnet down a copper tube. The tube will allow the currents to flow fully and as a result a strong opposing field will be set up. The magnet will be pulled downward by gravity and pushed upward by the opposing magnetic field as it drops down the tube. And, because this effect is proportional to velocity the opposing force will act as a damping force.

 

Note that in the equation, the mass reaches terminal (maximum) velocity almost immediately. This means that in the equation above the acceleration of the mass can be assumed to be negligible.

• Prelab:

1. Coil pickup sensors will be placed at three fixed positions on a copper tube. We will be able to measure when the magnet passes these points. Develop the equation(s) needed to approximate the damping coefficient. Hint: use the approximation techniques we used earlier in the course for estimating acceleration.

2. Create a Mathcad worksheet to record values in.

• Procedure

1. Measure the masses of the magnets on a scale (remember, be careful; these magnets are strong). Also measure the masses of the steel weights.

2. Measure the distances between the centers of the pickup coils on the copper tube. The magnet will pass by these points and we will be able to measure when.

3. Set up the oscilloscope/LabVIEW to determine when the magnet passes through the coils.

4. Drop the magnet through the tube and record the times it passes between the coils.

5. Measure the time differences and use the Mathcad sheet to estimate the damping coefficient.

6. Add steel masses to the magnet in various combinations, and determine the damping coefficients.

• Post-lab:

1. Develop a graph relating mass and velocity.

• Submit:

1. All work and results.

3.6 Lab 7b: Thermal Delay

• Objective:

To investigate a system involving thermal energy. We will observe a first order response for heat dissipation.

• Theory:

Masses have the capacity to absorb heat energy. Each type of mass will store and conduct heat energy at different rates. But, at all times the heat must be conserved. The figure below illustrates an enclosed mass with an internal coil of heating wire as a heat source. If we measure the current and voltage in the circuit, we can determine the electric power being delivered into the coil. If the enclosure is well insulated, then the electric power converted to heat will be absorbed by the enclosed mass. The temperature of the mass can be monitored with a thermocouple.

 

• Prelab:

1. For the thermal capacity for steel and paraffin wax.

• Procedure

1. Allow the steel block and wax to equalize to room temperature.

2. One at a time, cover the blocks with an insulating cover. Connect a power supply to the heating coil (along with an ammeter). Connect the thermocouples to the computer.

3. Build an amplifier for the thermocouple using the circuit and components supplied in the lab.

4. Turn on the power supply at different voltages and start measuring temperatures with LabVIEW. Calculate the power inputs using voltage and current.

5. After the blocks have suitably heated, turn off the power supplies and calculate the K values for each block.

6. Remove the thermal covers and measure the temperature drop using LabVIEW.

• Post-lab:

1. Find the time constants for the delay between the internal and external temperatures of the blocks using the data saved by LabVIEW.

• Submit:

1. All work and results.

3.7 Tutorial: Feedback Kit Overview

• The Feedback Controller kit contains a number of basic components to use in a simple control system. These components can be connected to form complete control systems. There are two types of control systems that we want to investigate, proportional and PID. Proportional control is one of the simplest types. When we add Integral and Derivative components (to get PID), this becomes more complete and able to respond faster and reduce long-term (steady state) error. The connection diagram below shows the general connections of the components for both controllers

• Cautions:

1. Do not mix modules from the different boxes. There are two different types of kits, and the motor types are not compatible.

2. TURN OFF the power before rewiring modules.

3. Don’t over tighten shaft couplers.

• The components include:

a base and hardware for connecting and securing components: the modules are all magnetically mounted to the base plate. There are couplers to connect motors shafts, etc.

DC permanent magnet motor: two of the kits contain permanent magnet motors. We can apply a single voltage that will cause the motor to turn.

DC separately excited motor: this motor is used in two of the kits. A separate coil is used to generate the magnetic field (in place of a permanent magnet). But, these motors do require that a separate voltage be applied.

power drive amplifier: this amplifier take in a voltage (low power/current) and supplies the same voltage (higher power/current) out to drive a motor.

tachometer: measures the speed of the motor by suppling a voltage proportional to the speed of the motor. This is actually a small DC motor.

magnetic brake: will slow the motor.

inertia disk: adds a moment of inertia to slow the motor’s response.

potentiometer (for position input): this potentiometer is provided so that an arbitrary input position may be specified for the control system.

summing (actually subtraction) circuit: subtracts the motor position from the input potentiometer position to get a difference.

preamplifier: this stage filters out noise and allows bidirectional motor rotation.

controller: proportional: also called the op-amp module, this will multiply the input.

controller: PID: a full controller for performing the PID function.

power supply, +24V, +/-15V: this provides the power required to drive all of the electronics and motors in the kits.

gearbox: reduces the speed and displacement of the motor shaft.

potentiometer: for position measurement and feedback.

• A basic system connection is shown below,

 

3.8 Lab 8b: Active Electrical Circuits

• Objective:

To investigate a system that introduces power into ’closed’ systems.

• Theory:

Basically, an active function delivers energy to a system at an unnatural rate (ie, higher than first order). The examples below are for op-amps used for a low and high pass filters.

 

 

• Prelab:

1. Develop transfer functions for the two filters in the theory section. Plot the Bode plot of the function in Mathcad using component values that you select.

2. Set up a Mathcad sheet to record and graph values for frequency plotted against the gain (i.e., ratio of input sine wave to output sine wave). Hint: You can draw the Bode plots easily by using the Fourier substitution.

3. Calculate the response of both filters to a step function input.

• Procedure

1. Set up the low pass filter using the component values Ri=10K, Rf=10K, C=10uF. Use a signal generator to input a sine wave into the filter. Measure the inputs and output magnitudes using an oscilloscope and enter the data values into Mathcad. There is a Labview vi that will do this for you.

2. Plot the response of the filter to a step input.

3. Repeat steps 1 and 2 for the high pass filter.

• Post-lab:

1. Compare the ideal transfer function to the actual function collected in the lab.

• Submit:

1. Transfer functions for both filters.

2. Theoretical Bode plots for both filters.

3. Experimental values for both filters.

4. A discussion comparison of both filters.

3.9 Experiment 8b: Servomotor Positioning Control Systems

• Objective:

To investigate simple position proportional servo motor control.

• Theory:

Recall the differential equation for motor velocity. And also the relationship between angular velocity and position.

 

We can develop a simple control technique for control of the position using the equation below. For this form of control, we need to specify a desired position by setting a value ’Vd’. The difference between the desired position and actual position is calculated (Vd-Vi). This will give a voltage difference between the two values. This difference is multiplied by a constant ’K’. The value of ’K’ will determine how the system responds.

 

The basic controller is set up as shown in the figure below. We can use a Labview program to implement the basic control equation described above.

 

• Prelab:

1. Develop a Mathcad document that will model the feedback controller given, motor parameters, desired position, an inertial load, and a gain constant. This is to be solved three different ways i) with Runge-Kutta integration, ii) integration of differential equations and iii) with laplace transforms.

2. Test the controller model using a step function.

• Procedure

1. Set up a labview program similar to that used in a previous lab. Apply a step function input and record the response.

2. For several values of proportional gain ’K’, measure the response curves of the motor to a step function.

• Post-lab:

1. Compare the theoretical and actual response curves on the same graphs.

2. Find and compare the time constants for experimental and theoretical results.

• Submit:

1. All work and results.

3.10 Lab 10: Advanced Control

• In the previous lab we used hardwired components to control the motor. In this lab we will use LabVIEW to replace the controllers.

Objective:

To position a DC motor using a proportional controller.

Pre-Lab:

1. Develop a LabVIEW interface for a feedback controller that will read the position of a motor shaft using a potentiometer, and then position the motor with an analog output voltage. The diagram for this controller can be seen in procedure step 3.

Equipment:

PC with LabVIEW and DAQ card

Interface cable

741 op-amp

3@ 1K resistors

TIP 31 NPN transistor

TIP 32 PNP transistor

2@ 15 uF electrolytic capacitors

12VDC motor

Potentiometer

Protoboards

Wires

+/-12V supply

Procedure:

1. Wire the motor control servo amplifier. Connect the amplifier input to a potentiometer to test the motor driver circuit. After testing and debugging is complete, disconnect the potentiometer and connect the servo amplifier to the analog output of the computer. Test the connection using the DAQ Configure program.

 

 

2. Connect the large potentiometer to the analog inputs for the computer, and use the +/- 12V supply. Test the input range using LabVIEW. Connect the potentiometer and motor shafts together with a piece of hose. In this configuration the potentiometer voltage will be proportional to the angle of the motor shaft.

 

3. Enter the LabVIEW interface developed in the prelab to control the motor position. Run the program to see if it is operational.

 

4. Characterize the performance of your proportional controller.

3.11 Lab 10b: PID Control

Objective:

To position a DC motor using a PID controller.

Pre-Lab:

1. Examine materials in the notes on PID controllers.

2. Develop a LabVIEW program for a feedback controller that reads position from a potentiometer, and will position the motor with a PID algorithm.

Equipment:

PC with LabVIEW and DAQ card

Interface cable

741 op-amp

3@ 1K resistors

TIP 31 NPN transistor

TIP 32 PNP transistor

2@ 15 uF electrolytic capacitors

12VDC motor

Potentiometer

Protoboards

Wires

+/-12V supply

Procedure:

1. Wire up the motor control circuit as used in the previous lab.

2. Use the proportional controller to test your setup.

3. Design and implement a full PID controller in LabVIEW and test.

4. Change the parameters and determine the effect.

5. Characterize the performance of your PID controller.

3.11.0.1 - Lab 10c: Controller Programming 3.12 Objective:

To implement a control program in a programming language.

Pre-Lab:

1. Review the manuals for the Basic Stamp II.

2. Examine the programs in the course notes.

3. Develop a discrete equation for the controller.

Procedure:

1. Wire up the power amplifier used in the previous labs.

2. Enter your program into the basic stamp chip and test for operation.

3. Modify the parameters and determine the effect of the variations.

Marking:

40% Prelab

30% PID controller

30% analysis of results

3.13 Lab 11: Electronic Control Systems

Objective:

To design and build a control system that compares analog values and generates an analog control voltage. The position of a motor will be controlled.

Theory:

In a standard control system we can specify a target position as an input: setpoint. We can compare this target position to the actual position and calculate the difference: typically called the error. In a simple control system we can generate a voltage proportional to the error this will tend to move the drive the motor forward or backwards to the goal. As expected, we need to isolate the control electronics from the power requirements of the motor. To do this we will use an amplifier. The general layout for the system is shown below.

 

The difference and proportional stages can both be implemented using op-amps. The amplifier can be implemented using a simple PNP/NPN transistor pair as shown below.

 

 

With this controller there are a number of issues that will arise. First, the motors that we will use will not have a speed proportional to voltage. In fact they will not even turn below a certain voltage. We can reverse the direction of the motor by reversing the voltage applied.

Second, the stages of the control system will all be limited by the supply voltages. If the proportional gain is larger than ‘1’ then we will have the potential to generate a control signal that is beyond the supply voltages. When this occurs it will clip the controller signal (making it non-linear). If we have a very large gain we will have the controller turn fully on in one direction, or the other. The effect will be that the motor is always hunting for its zero position.

Prelab:

1. Design the circuitry for the difference stage using an op-amp. This should be a simple subtraction circuit.

2. Design the circuit for the proportional multiplication stage using an op-amp. This should multiply the error by some value: called the gain. Make the gain variable for the approximate range from 0.1 to 100.

3. Design and build the controller stages

Procedure:

1. Test the voltage speed ratio for the motor while unloaded. Apply various voltages and measure the rotation speed. You can do this by counting the number of rotations over a long period (say 30 seconds). Do this for voltages from -12V to +12V, and draw a graph.

2. Connect the motor back to the circuit built in the prelab, and check for operation.

3. Set the proportional gain low (less than 1) and turn the input potentiometer. Set the gain near 1 and sweep the potentiometer again. Set the gain high and sweep the input one last time. Write an observation about the differences.

4. Set the proportional gain to ‘4’ (compare input and output voltages to find). Replace the input potentiometer with a signal generator. Set the generator to 0.25 Hz, and an amplitude of +/- 3V. Sketch the inputs and corresponding outputs (motor positions) for sinusoidal, triangular, and square waves.

5. Set the input to a sinusoidal wave. This time you need to sweep the frequency of the wave. At various values record the amplitudes and phase shift between the input and output. Draw a Bode and phase plot for these values and develop a transfer function.

Submit:

1. The circuit designs.

2. The motor voltage speed graph.

3. Sketches of various input/output wave forms.

4. The Bode plot, phase plot and transfer function for the controller.

Objective:

To investigate the effect of adding integral and derivative elements to a control system.

Theory:

Components can be added to the basic proportional control system to improve the response to changes in desired positions and velocities. In the previous lab you will have noticed that the motor never moved to the requested position. In the previous control system (Proportional) we can increase responsiveness (using derivative) and long term error response (using integral).

 

We can develop integrators and differentiators using opamps. Two circuits are shown below for integration and differentiation.

 

Prelab:

1. Design circuits for the integrator and differentiator using op-amps. These should have adjustable gains and select time constants based on your experiences from the previous lab. It is also recommended that you do not use inductors.

2. Construct the controller circuitry.

Procedure:

1. Test the circuitry for basic functionality.

2. Vary the PID gains and record the response. Calculate the rise time, overshoot, and settling time. Use these to calculate a transfer function.

3. Adjust gains, and recalculate the values until the system has a critical damping factor (=1).

Submit:

1. Complete designs for the controller.

2. A table of gains, response plots, response parameters and a transfer function.

Objective:

The use of PWM to control position and velocity will be explored.

Theory:

Using analog values for control can be inefficient and hard to implement in a digital system. A popular alternative is to deliver an effective voltage by changing the duty cycle of a full amplitude wave. When the duty cycle is 100% the voltage has the full effective value. When the duty cycle is 50% we only deliver 50% of the effective power, etc. We can generate a waveform of this type using a circuit like that below.

 

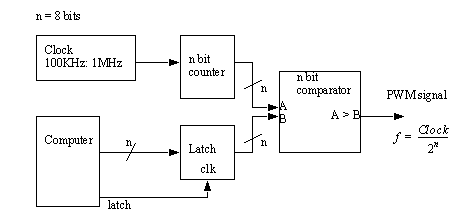
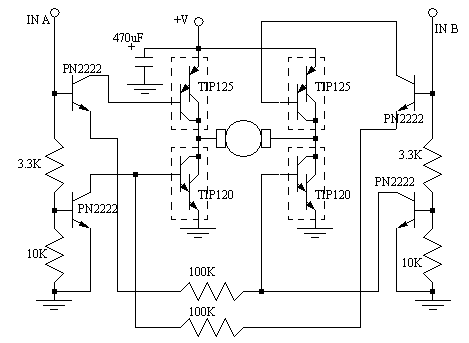
This system will cycle continuously, and a fast stable clock will result in high precision signal. The signal from this will be on or off, and as a result we will want to use a different type of power amplifier than was used before. the H-bridge circuit shown below (from http://www.bobblick.com/bob/projects/hbridge by Bob Blick) has four symmetrical Darlington coupled BJTs (TIP 125s and TIP 120s) used for controlling motor direction and switching current. The other transistors are used for driving these power transistors. To drive the circuit there are four possible states on INA and INB. If both are off the outputs will float: this means that the motor windings are open circuits, and the motor can be turned freely. If the inputs are both high then the windings are shorted and this will cause motor braking. If we want to turn in one direction we will apply the pulses to either INA or INB. When supplying pulses we want to hold the other input low.

 

We can detect motor velocity using a tachometer. There are numerous types available. One of these uses a small DC motor that will generate a voltage when the shaft is turned. We can also attach a small magnet to the shaft, and use a stationary coil of wire to generate a pulse as the magnet travels by. This signal can then be integrated to provide a voltage. Or, the duration between pulses can be measured to estimate the velocity. We could also use an encoder.

Prelab:

1. Design and build the PWM signal generator. You can use discrete ICs or you can create an Altera based design.

2. Build the H-bridge circuit and interface it to the PWM chip.

3. Pick a computer to use (Basic Stamp, IBM PC, 68HC11, etc.) and interface it to the PWM circuit.

4. Select, design and connect a tachometer circuit to the motor, and design a signal conditioner to input the velocity to the computer.

5. Write a computer program to drive the control loop.

Procedure:

1. Test the circuit and assure that it is operational.

2. Tune the circuit for critical response.

Submit:

1. A completed design.

2. A discussion of test results.

Objective:

To design and build a synchronous motor drive.

Theory:

We can drive an AC motor by synthesizing an AC signal. By controlling the frequency of the generated AC wave we can control the speed of the motor. A simple approach to generating the synthesized wave is shown below. This technique uses a ROM/EPROM/whatever to store the wave values. We then use a clock and counter to step through the values. As we increase the number of bits in the system we get more accuracy. The values stored in the ROM should be for a sine wave over a full 360 degree cycle.

 

The programmable divider can be designed around a simple counter and comparator, much like the previous PWM design. The figure below illustrates the basic layout. For this divider the value from the computer will range from 0 to (2**n)-1.

 

A low pass filter can be developed with the basic form shown below. The resistors on the inverting input allow it to be biased so that the filter can work with a unipolar supply. A transfer function can be developed and then used to select values more appropriately.

 

Prelab:

1. Design and construct the circuitry. Use discrete components and/or Altera chips.

Procedure:

1. Connect the circuit to a synchronous motor and test the circuit.

2. Vary the frequency of the generator and measure the frequency of the motor using the strobe tachometer.

3. Generate a graph comparing actual and requested over a range of values.

Submit:

1. The completed design.

2. A graph relating unloaded frequency input and actual motor frequency.