
• Can be done by an individual, or a team
• Consider a production team about to launch a new product. They must anticipate factors that will affect the final product
APPROACH: Use a Cause and Effect Diagram
• The cause and effect diagram was developed by Kaoru Ishikawa in 1943.
Commonly called: Cause and Effect (CE), Ishikawa Diagram or Fishbone diagram
• In quality we use these to find factors that have some role in a good/bad quality.

• For manufacturing there are some more standard causes to consider.
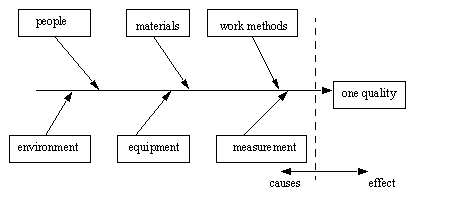
• How can a CE diagram be made up?
• Brainstorming is a two stage process
Step 1: As a group, have each team member contribute ideas. If an idea is not good it doesn’t matter. Add ideas to the diagram. Exhaust all ideas! NO CRITICISM!!!
Step 2: Review the diagram critically as a group. Voting will help to narrow down what are the most important factors.
Post it in visible spots for common reference by all the workgroups.
Use it to anticipate, or find the cause of problems.
Keeps workers involved and informed.
Analysis: allows tracking of errors, efficient use of resources, lower costs.
Elimination of unwanted causes.
Standardization of existing and proposed operations.
Education and training to allow personnel to make decisions and correct problems autonomously.
• Another type of CE diagram is the Process-Analysis diagram. This is used when there are a number of operations or factors involved.

• When considering CAUSES, there are two main types, assignable and chance.
chance: normal, or natural variations that occur in a system (e.g. dice)
assignable: controllable parameters such as material, process parameters, operator skill, etc.
• After the CE diagram is constructed we can start to trace the cause of problems.
1. We have collected data from defects on the factory floor.
2. We have identified the causes of each of the defects (could also use problems, type of problems, etc)
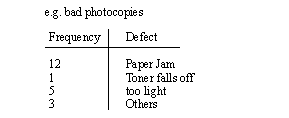
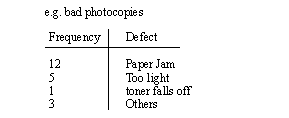
4. Draw the graph (** This is a Pareto diagram)
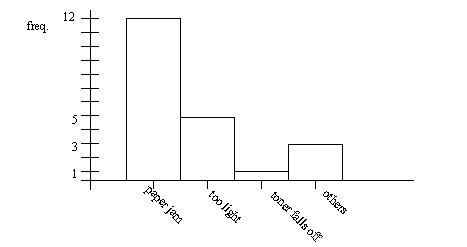
5. Tackle the problem on the left first. Paper jams are the most significant problem that comes up.
• It is also possible to use the concept in the Pareto Diagram, in a setting with multiple processes.
1. Take data concerning quality.
2. Assign causes and make a table, then sum columns and rows


• Developed by Dr. A.V. Feigenbaum in the 1950’s at G.E.
• Includes all level of management.
• quality should be first and foremost in everyones minds
• In the production cycle the quality control activities are defined as,
- engineering quality products
- receiving and inspecting quality material
- Manufacturing quality parts and products
- inspecting and testing quality products
- installing and servicing quality products
• Basic requirements for implementation,
1. Management must re-emphasize the quality responsibilities, and accountabilities of each employee, regardless of position
2. Create a Quality Department that will be responsible for the maintenance of quality.
• These set the tone for the modern concern with quality [get first ref]
1. Innovate and allocate resources to fulfill the long-term needs of the company and customer rather than short-term profitability.
2. Discard the old philosophy of accepting nonconforming products and services.
3. Eliminate dependence on mass inspection for quality control; instead, depend on process control, through statistical techniques.
4. Reduce the number of multiple source suppliers. Price has no meaning without an integral consideration for quality. Encourage suppliers to use statistical process control.
5. Use statistical techniques to identify the two sources of waste -- system (85%) and local faults (15%); strive to constantly reduce this waste.
6. Institute more thorough, better job related training.
7. Provide supervision with knowledge of statistical methods; encourage use of these methods to identify which nonconformities should be investigated for solution.
8. Reduce fear throughout the organization by encouraging open, two-way, non-punitive communication. The economic loss resulting from fear to ask questions or reporting trouble is appalling.
9. Help reduce waste by encouraging design, research, and sales people to learn more about the problems of production.
10. Eliminate the use of goals and slogans to encourage productivity, unless training and management support is also provided.
11. Closely examine the impact of work standards. Do they consider quality or help anyone do a better job? They often act as an impediment to productivity improvement.
12. Institute rudimentary statistical training on a broad scale.
13. Institute a vigorous program for retraining people in new skills, to keep up with changes in materials, methods, product designs and machinery.
14. Create a structure in top management that will push every day for continuous quality improvement.
• A quality philosophy that reaches all levels of an organization.
• There is no well defined standard.
• One tool to help assessment of problems is the list of questions below, [Nordeen, 1993]
1. Why does the product have poor quality and/or why does the service of the product have poor quality?
2. Why was the product not correct and/or why was the service of the product not correct?
3. Why was the total process for developing and producing the product and its relatedd systems not capable, and why did the people not have the required knowledge and skills?
4. Why is the importance of the organizational processes, knowledge, and skills not recognized in the business plan and management of the organization?
5. Why does senior leadership not understand?
4.1 Nordeen, D.L., “Total Quality Management in Industry”, Automotive Engineering, June 1993, pp. 35-41.
• After control charts (X and R) have been developed, and the process is in control, the process capability is 6σ
• The capability index can be calculated for a design

• The capacity Ratio can also be calculated
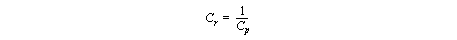
• The Capability Index is another useful measure
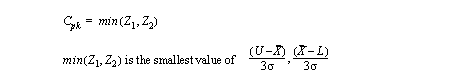
• Some general notes about these indices
Cp is independent of process center
Cp = Cpk when the process is centered
Cpk of 1 means the process is OK
Cpk < 1 means product out of spec
Cpk = 0 process center at a tolerance limit
Cpk < 0 process center is outside the tolerance range
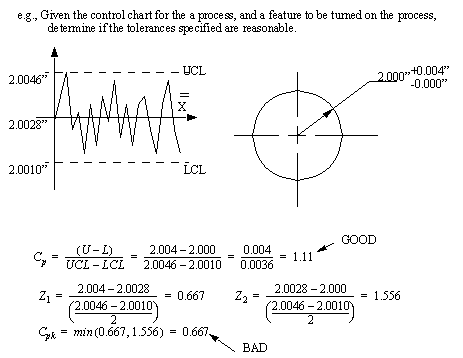
• If Cp or Cpk are both too large (>>2) the process may be too good, suggesting less expensive, easier processes could be considered.
• A good rule of thumb for using Cp and Cpk is that if new equipment is being purchased, try to get values above 1.5, if the equipment is already available, 1.33 is acceptable.
• Try Probs #6 pg124, #32,33 pg128
• A strategy to target quality problems

• This can be summarized as 6σ of variance alone ignores the drift of the process center. Assuming the process center varies by +/-1.5σ results in a more accurate model of production.
• The steps in implementation are,
1. Identify critical characteristics through such functions and activities as marketing, industrial design, R&D engineering, etc.
2. Identify the product elements that influence the critical characteristics defined in step 1.
3. Define the process elements that influence the critical characteristics defined in step 2.
4. Establish maximum tolerances for each product and process element defined in steps 2 and 3.
5. Determine actual capability of the elements presented in steps 2 and 3.
6. Assume Cp >= 2 and Cpk >= 1.5.
• WHAT? combinations of individual parameters for process control are varied, and their effect on output quantities are measured. From this we determine the sensitivity of the process to each parameter.
• WHY? Because randomly varying (trial and error) individual parameters takes too long and the results are not mathematically conclusive.
• e.g. A One-Factor-At-A-Time-Experiment

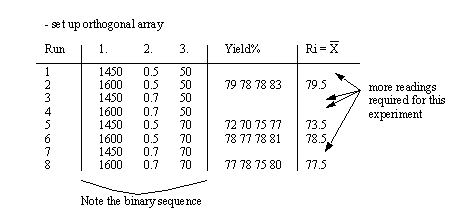
• The example shows how the number of samples grows quickly.
• A better approach is designed experiments
• These experiments vary parameters with the basic procedure below,
1. Identify process variables (inputs) and Dependant variables (outputs). Outputs should be continuous values.
2. Select discrete values for the inputs. The most basic approach is to pick a high and low value for each.
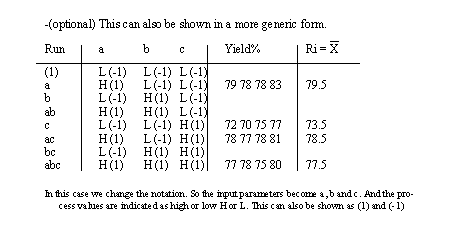
3. Create a data collection table that has parameters listed (high/low) in a binary sequence. Some of these tests can be left off (fractional factorial experiment) if some relationships are known to be insignificant or irrelevant.
4. Run the process using the inputs in the tables. Take one or more readings of the output variable(s). If necessary, average the output values for each of the experiments.
5. Graph the responses varying only one of the process parameters. This will result in curves that agree or disagree. If the curves agree then the conclussion can be made that process variables are dependent. In this case the relationship between these variables requires further study.
6. Calculate the effects of the process variable change.
7. Use the results of the experiment to set process parameters, redesign the process, or to design further experiments.
• e.g. 3-factorial DOE for springs in last section



4.3 Harry, M.J., “The Nature of Six Sigma Quality”, A booklet published by the Motorola Inc. Government Electronics Group,
4.4 Toper, W.G., “The ISO9000 Quality System Standards and Their Implication for Global Business”, A tutorial presented at the third annual IIE Four-chapter Conference at the Sheraton Falls view Hotel & Convention Center, Niagara Falls, Ontario, Canada, June 14, 1993.