9. Trusses and Frames

• We will look at a variety of analysis techniques for trusses and frames. These techniques endeavor to find the internal forces in trusses, and external forces for frames.

• Trusses are at the heart of many engineering projects. We can see one of these in the bridge across the grand river.

[picture]

• Basically, a truss is a collection of beams joined together to carry simple and complex loads.

• We can see trusses use in cranes,

[picture]

[picture]

• Trusses are typically made from beams that are joined with gusset plates.

[picture]

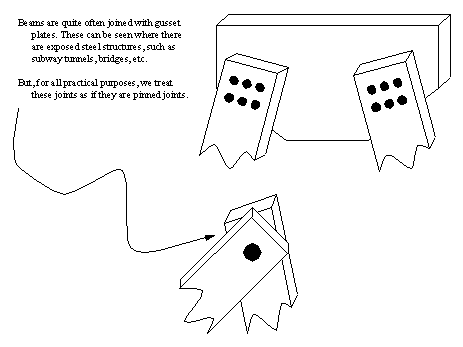
• Other times obvious pin joints are used. Consider the pin joint on the end of the tension member below,

[picture]

• With these types of problems the tension or compression of the beams/members should be clearly indicated. Materials and structures will not fail at the same load when in tension (necking then fracture), than in compression (buckling).

• We can see a tension member in a bridge with turnbuckles for tensioning,

[picture]

• The basic assumptions used in most truss and frame problems are,

1. the joints have pinned ends, so the forces exerted by the beam has a direction that is along the line between pins.

2. Forces are exerted at pins, but no moments.

• Types of trusses are shown below,

[picture]

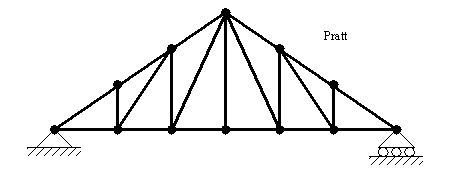
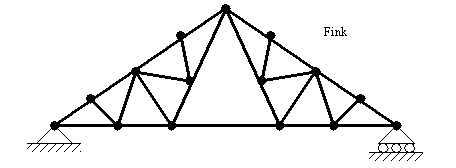
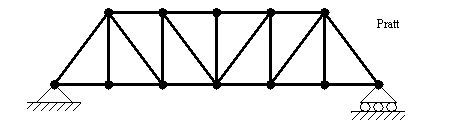
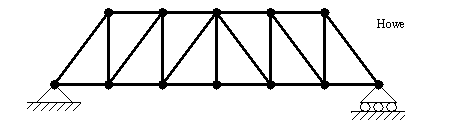
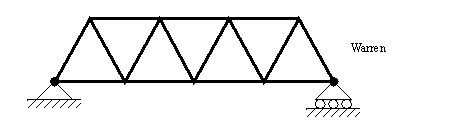
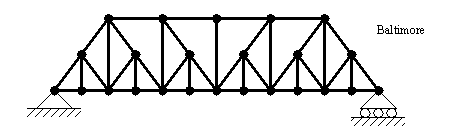
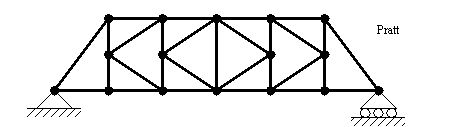
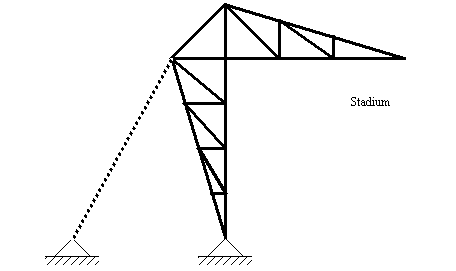
• Picture of other types of trusses can be seen below,

[picture]

[picture]

• Many of the methods in this section can also be extended to the analysis of trusses in 3D.

[picture]

9.1 Beer, F.P., Johnson, E.R., Statics & Mechanics of Materials, McGraw-Hill, 1992.

9.2 Hibbeler, R.C., Engineering Mechanics: Statics and Dynamics, 6th edition, MacMillan Publishing Co., New York, USA, 1992.

• Trusses are composed of beams and pin joints. Generally, if the frame is constructed of only triangles (internally) it will be stable. (not collapse when pushed the wrong way)

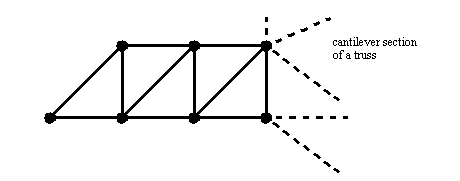
• Quite often additional members are added to frames to stiffen it (make it stable), but not to carry loads. We can see such members in a bridge,

[picture]

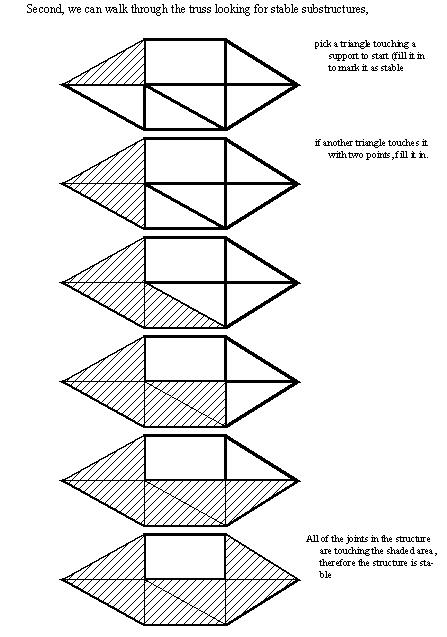
• We can predict stability using a basic topological relationship where we look for equality. The equation shown below requires that the truss be composed of simple pinned beams, and when drawn to scale on paper the beams must not cross or touch except at the pinned joints

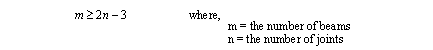
• We can also verify stability by making nodes that are held in place either by supports, or triangular structures.

• As an example,

[working model file]

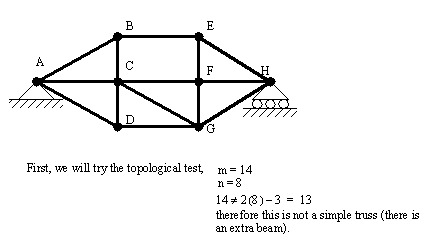
9.3 Beer, F.P., Johnson, E.R., Statics & Mechanics of Materials, McGraw-Hill, 1992.

• The basic steps when solving problems with the method of joints is,

1. Draw an FBD for each joint as if it is a particle.

2. Solve for the applied forces with the “joint particle” in equilibrium. The simplest joints are often the best to start with.

• We can see an example of a two force member below being used to support a canopy,

[picture]

• This method is best shown using a sample problem, ([Hibbeler, 1992], prob 6-7, pg. )

[picture]

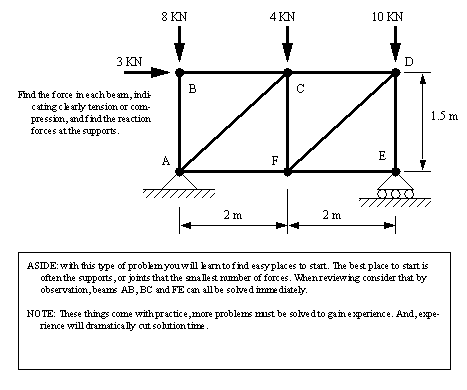
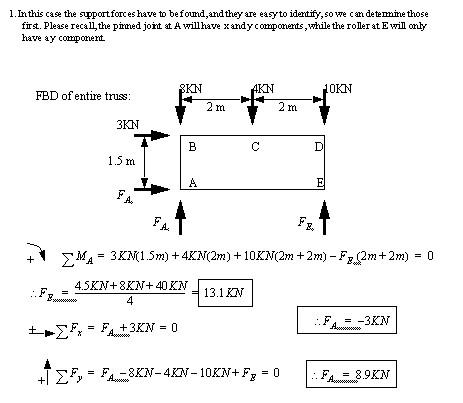
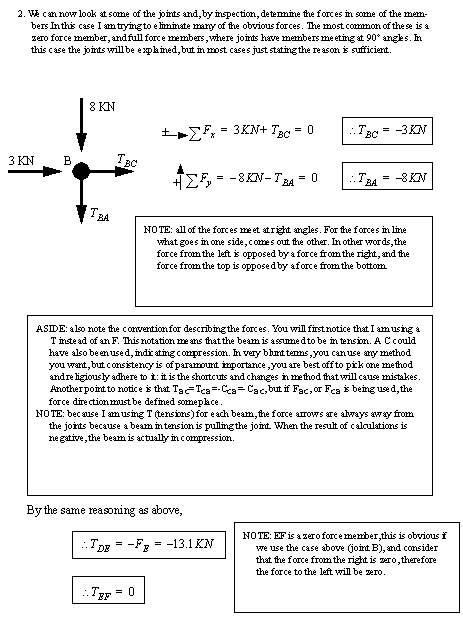
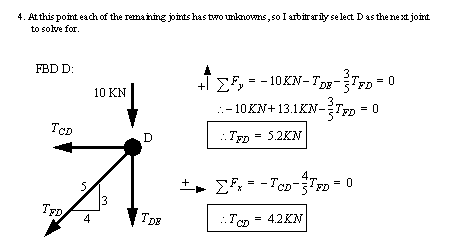
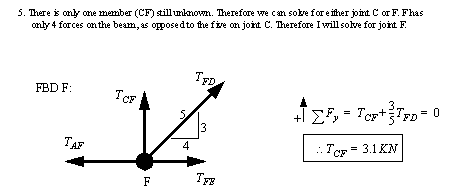
• This problem can also be solved using matrices techniques by framing the truss members as linear equations.

Problem 9.1 Use the method of joints to find the force in each member of the truss below.

Problem 9.2 Determine the force in each member of the truss shown. Indicate tension or compression.

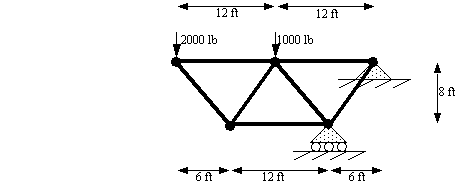
Problem 9.3 Determine the force in each member of the truss shown. Indicate tension or compression.

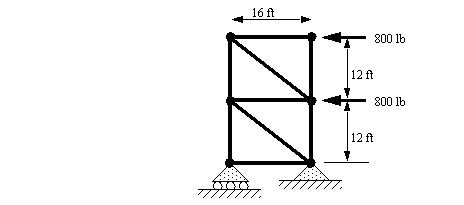
Problem 9.4 Find the forces in each of the beams of the structure below (indicate tension or compression). Assume all joints are pinned.

Answer 9.4

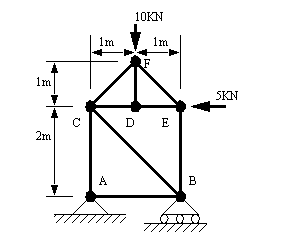
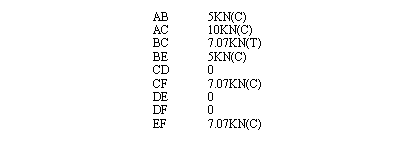
Problem 9.5 For the frame below, find the tension/compression in each member, under the loading conditions given, and assuming all joints are pinned. (Note: you must clearly indicate tension or compression when dealing with this type of problem)

Answer 9.5 EF=515lb(C), BC=515(C), CD=125(C), AB=774(T), AE=401(C), BD=1563(T), BE=625(C), DE=1289(C)

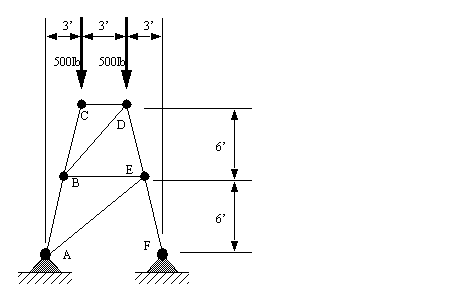
Problem 9.6 Given the frame below, find the tension/compression in each member.

Problem 9.7 Find the forces in each beam of the bridge shown. (As usual, clearly indicate tension or compression)

Answer 9.7

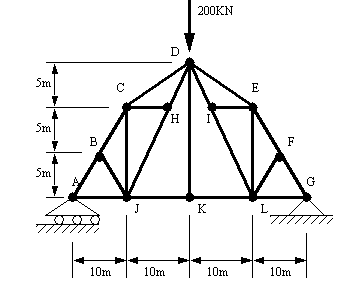
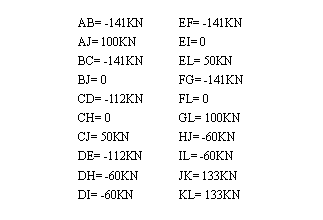
Problem 9.8 Find the tension/compression in each member of the frame below, (HINT: look for 6 zero force members and use symmetry)

Answer 9.8

9.3.2 References

9.4 Beer, F.P., Johnson, E.R., Statics & Mechanics of Materials, McGraw-Hill, 1992.

9.5 Hibbeler, R.C., Engineering Mechanics: Statics and Dynamics, 6th edition, MacMillan Publishing Co., New York, USA, 1992.

9.4 The Method of Sections

• Basically: cut out a part of a truss, and then treat it as if it is a rigid body. When done wisely, this allows simplified solutions. The alternative is using the method of joints to find all (or many) of the forces in the frame.

• Keep in mind that while moments are very popular with the method of sections, it can also be used for forces as well.

• Consider an example where we want to find forces in a structure, ([Hibbeler, 1992], prob 6-24, pg. )

 

 

 

 

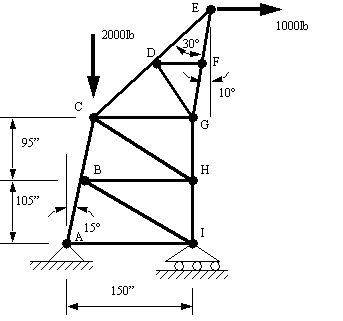
Problem 9.9 In the frame below members DL and EL can support up to 1kip of tension or compression, find the maximum load P that may be applied. (Hint: you could mix the method of joints and sections)

9.4.1 Problems

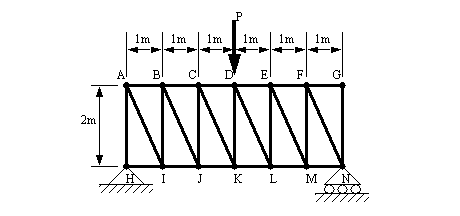
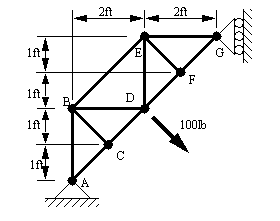
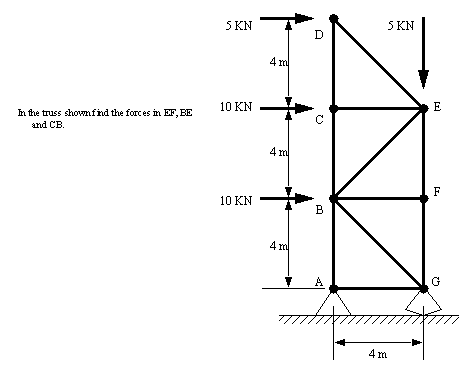
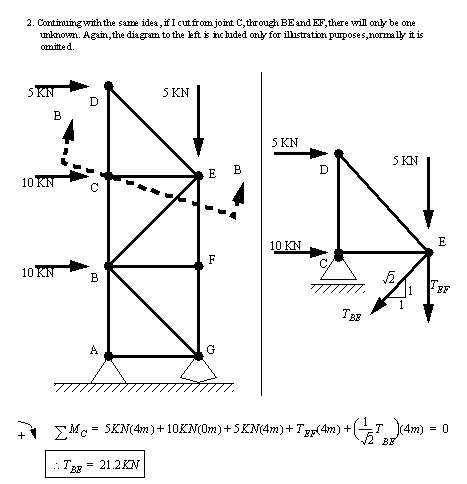
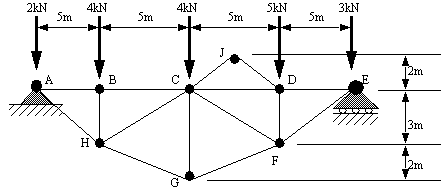
Problem 9.10 Determine the tensions/compressions in members EF, JK and HJ for the bridge truss shown below. The method of sections is recommended.

Problem 9.11 Find the forces in FG and DF (indicate tension or compression). Assume all joints are pinned.

Answer 9.11 AH=1.77kip(C), FG=0)

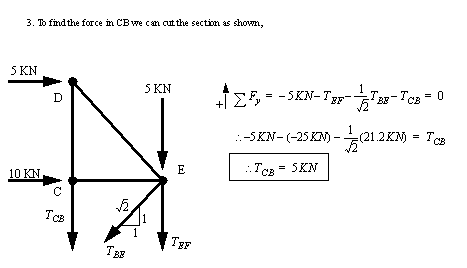
Problem 9.12 In the frame pictured below, find the forces in DE, EF, DF and CB.

Answer 9.12

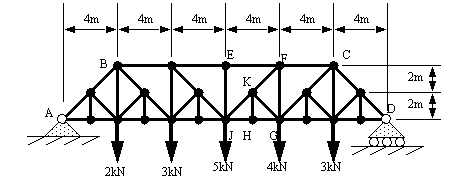
Problem 9.13 Find the forces in members CD, CF, CG. (You will benefit most by using the method of sections to solve this problem)

Answer 9.13 CD= 11.25KN(C), CF= 3.21(T), CG= 6.8(C)

Problem 9.14 Find the forces in JM and KM.

Answer 9.14 JM=83KN, KM = 14KN

Problem 9.15 Find the tension/compression in members CE, DE.