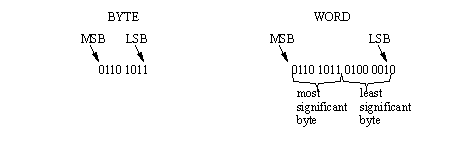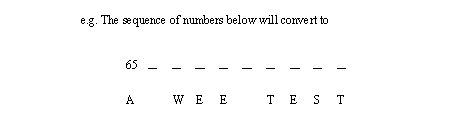1.2.1 Binary

 

• Binary is best used in computers because signals are ON/OFF which is well suited to the two binary digits.

 

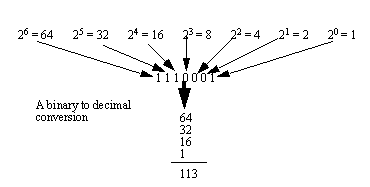
• Converting between number systems can be done by looking at digit magnitude.

 

 

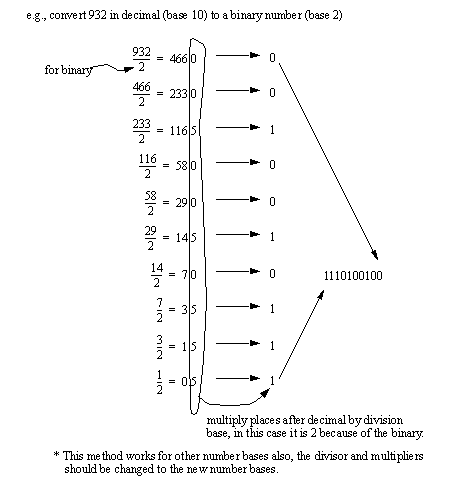
• Conversion can also be done between systems by division.

 

• For division use remainders.

 

 

• Convert the following numbers to/from binary

 

 

• Binary bytes and words are shown below.

 

 

 

1.2.2 Boolean Operations

 

• In most discrete systems the inputs and outputs (I/O) are either on or off. This is a binary state that will be represented with,

 

1 = on

0 = off

 

• Because there are many inputs and outputs, these can be grouped (for convenience) into binary numbers.

 

• Consider an application of binary numbers. There are three motors M1, M2 and M3

100 = Motor 1 is the only one on

111 = All three motors are on

in total there are 2n or 23 possible combinations of motors on.

 

• The most common Binary operations are,

 

 

 

1.2.3 Binary Mathematics

 

• These include standard logic forms such as,

- and/or/add, etc.

- compliments

 

• Negative numbers are a particular problem with binary numbers. As a result there are two common numbering systems use,

- signed binary - the most significant bit (MSB) of the binary number is used to indicate positive/negative

- 2s compliment - negative numbers are represented by complimenting the binary number and then adding 1.

 

• Signed binary numbers are easy to understand, but much harder to work with when doing calculations.

 

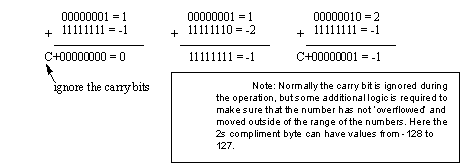
• An example of 2s compliments are given below,

 

 

• When adding 2s compliment numbers, additional operations are not needed to deal with negative numbers. Consider the examples below,

 

 

 

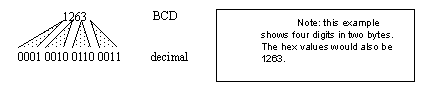
1.2.4 BCD (Binary Coded Decimal)

 

• Each digit is encoded in 4 bits

 

 

• This numbering system makes poor use of the digits, but is easier to convert to/from base 10 numbers. For the two bytes above the maximum numbers possible are from 0-9999 in BCD, but 0-64285 in binary.

 

• Convert the BCD number below to a decimal number,

 

 

• Convert the following binary number to a BCD number,

 

 

 

1.2.5 Number Conversions

 

• Convert the following binary number to a Hexadecimal value,

 

 

• Convert the following binary number to a octal,

 

 

 

 

1.2.6 ASCII (American Standard Code for Information Interchange)

 

• While numbers are well suited binary, characters don’t naturally correspond to numbers. To overcome this a standard set of characters and controls were assigned to numbers. As a result, the letter ‘A’ is readily recognized by most computers world-wide when they see the number 65.