Linux and Integrated Manufacturing
by Hugh Jack, Grand Valley State University
Introduction
Enthusiastic anticipation has been building for the arrival of integrated manufacturing systems. Many visionaries in the 1970s and 80s eagerly predicted ‘lights-out’ factories with workers replaced by autonomous robots. We are still far from that era.
The current state of integration is a collection of crudely interconnected components. For the most part, the low level hardware/software is proprietary and is difficult to interface to dissimilar equipment. However, various solutions exist for connecting these. The most common approach is to simplify (overconstrain) the control problem so that direct electrical connections between devices are sufficient. More mature users sometimes use personal computers with proprietary software to interact with a small number of devices. The most advanced systems are constructed by senior engineers and programers who write software to connect the devices in a distributed control system. Ideally it should be possible to exchange information and requests between all points in the system. Practically it means that there is a central database that is a commonly accessible point for storing information, and a network for communication. The design and implementation of an integrated manufacturing system is a complex task. It is also a task that is rarely addressed at a suitable level in undergraduate engineering programs.
An integrated manufacturing systems course was designed to introduce senior manufacturing engineering students to the architecture and design issues in a high level system. This course follows courses in low level control systems, such as PLCs and feedback controllers. The course uses manufacturing equipment such as PLCs, robots, CNC machines, material handling systems and vision systems. At the beginning of the semester students set up their own Linux servers, including software for a web server, database server, and a platform for C programming. Throughout the semester they are given readings and tutorials on various aspects of programming device drivers, interfaces and integration tasks. At the conclusion of the course the students apply their skills as a team to fully integrate a manufacturing workcell around a central SQL database.
This course replaces an older, more traditional version that used graphical Dos and Windows programs. By moving to Linux the students were able to produce a much more complex system in a shorter period of time. The paper is a detailed discussion of the course, a custom written textbook [1], and the student designed and built workcell.
Integrated Manufacturing
A manufacturing facility is a distributed set of processes. The objective is to move raw materials and work through the facility so that processes are applied in appropriate sequences to transform the work. After the required steps are completed, the work emerges as a product ready for shipping. To accomplish this, there are a variety of configurations used, such as flow lines and job shops. For practical reasons each function is made to operate independently even though they are part of a larger system. At the basic level, integrated manufacturing establishes methods for communication so that the independent processes act as a unified group. At the next level is the issue of how the information is handled.
A well organized system can be integrated using a well designed paper based system. However, as the size and complexity of the system grows, the paper becomes a bottleneck, a burden, and a source of failure. The limitations of paper based systems can be overcome with computers and networks. The disadvantage of computers and networks is a higher level of complexity. There is currently a shortage of professionals able to implement integrated manufacturing systems.
Despite the shortage of suitably trained personnel, the factory floor is ready for integrated manufacturing. Most new equipment has communication abilities that make it suitable for remote interrogation and programming. Unfortunately there is no off-the-shelf integrated manufacturing that is versatile enough to perform all of the required functions. Process control and monitoring software, such as Wonderware and Bridgeview, are available to simplify communication issues, but they don’t suitably address the information issues. At higher levels there are numerous business systems for scheduling and tracking manufacturing jobs, but these are typically disconnected from the processes. At present, developing an integrated manufacturing system requires a high level of knowledge and skill.
The lowest level of integration skills required includes an understanding of computer programming, networking, communications and databases. The engineer/programmer must also understand the basic components of these systems, such as robots, CNC (Computer Numerical Control) machines and PLCs (Programmable Logic Controllers). The intermediate level of integration requires knowledge of manufacturing organization and methods, such as ERP (Enterprise Requirements Planning). The high level of integration knowledge includes concepts of system architecture, and a knowledge of all the lower level components. At this point in time there are few engineers (or computer scientists) prepared to fulfil even the basic level of knowledge upon graduation.
What is Linux
Linux is a clone of Unix that is composed of two main parts, the kernel and the other ‘stuff’. The kernel is the heart of the operating system that runs programs and interacts with the hardware in the computer. It was initially developed by Linux Torvalds as a student in Finland in the early nineties. The other ‘stuff’ includes compilers, window managers, office software, networking software, etc. It was developed and provided by volunteers. The most significant contributor is the GNU project group. Linux is covered by the GPL (GNU Public License) that makes it free. This means that there is no cost to use (or resell) the software, and the software can be modified to meet the needs of subsequent users.
The freedom to modify Linux is the reason for it’s popularity. At present there are many different ‘versions’ in the form of ‘distributions’. For example, the Redhat distribution is an easy to install point-and-click oriented version ideal for beginning and intermediate users. More advanced users will select more mature distributions, such as Slackware. Regardless of which distribution is selected, the basic operation and software is the same across all platforms. By contrast, another popular operating system has different versions of operating systems, for desktop computers and embedded devices, but software is not interchangeable, and the systems behave differently.
Since the early nineties, Linux has grown to be the operating system of choice for servers. It has also become significant for embedded devices and desktop systems. The most telling trend is that it has become the operating system of choice for many of our highly motivated undergraduates. The fact that Linux is free now also means that it is being developed and supported by more companies and individuals than any other operating system. Examples of corporations supporting Linux are IBM, HP, Sun, SGI, Intel, AMD, Compaq, Netscape, Adobe, Oracle, etc.
The Course
The integrated manufacturing course (EGR 474) has been designed to meet the needs of local industries, many of whom are using extensive integrated manufacturing systems. The course is primarily intended for manufacturing engineering students, but it may also accommodate students in the electrical/computer emphasis or computer science. It is expected that all students have taken a C or C++ programming class previously. The manufacturing students have also taken courses covering topics such as scheduling, work flow and manufacturing data.
The course format uses three hour labs, twice a week. Students are expected to read the textbook [1] before class, and the class times are used for hands-on tutorials and exercises. The labs at the beginning of the course focus on basic devices and interfaces. The level of treatment is elevated until the end of the course when students perform a project to integrate a workcell. The list of course topics is below. It shows that early in the semester students set up their own servers and development platforms. These are then used in subsequent weeks to develop programs to communicate with devices, and interface to an SQL database. The typical format for weekly labs is to have students read the background material before arriving. The labs begin with tutorials that discuss basic concepts and methods. Students are then expected to write programs.
1. Installing Linux and setting up a web server
2. Basic C programming review - a number guessing game
3. An Introduction to SQL databases - using a command line interface
4. Using programs to communicate with an SQL database
5. Using C to communicate over the serial port
6. Exploring hardware - each student was given a different device
- each student wrote a device driver for the hardware used in 6.
- they presented the results to the class with a brief tutorial document.
The previous, non-Linux, version of the course was much less successful. It managed to cover many of the basic topics using individuals devices and software. But when it came to integrating the devices the integration of each device became a major task, without the possibility to reuse any knowledge. This is largely due to the philosophy of closed source desktop operating systems. In particular the systems are not designed to interact with other software outside the boundary of a single computer. Using Linux allowed the students to explore basic interface tools, and then use them to integrate the system easily in the final project.
The Project 
The project is used to provide a culminating experience. Students are challenged to select a task for a workcell and then develop the system from system architecture to implementation and testing. In the summer of 2001 the students chose to make pen holders that would be customized with an ‘S’ or an ‘M’ (for a couple of popular football teams). The architecture they developed is shown in Figure 1. The center of the system is an SQL database.
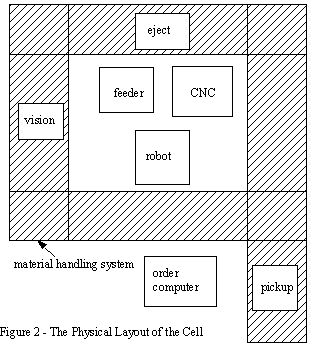
.The students designed the system to be based around a central SQL database. Each of the devices used the database to indicate their status to other devices, receive commands for work, or to issue commands to others for work. The system shown in Figure 2 is based around a material handling system which moves work on carts. The system contains a CNC machine, a robot, a DVT vision system and other functions controlled by Devicenet. An order is placed on a computer using a Web browser. The order is sent to a CGI program that enters the order into the database. The Devicenet controller watches the database and when an order is present a board is feed by cycling a pneumatic cylinder in the feeder. When a board is ready for pickup, and the CNC machine is idle, the robot will pickup the board, and load it into the CNC machine. The CNC machine then cuts the board as requested. When done the robot sees the board ready for pickup, and loads it into a cart. The cart is then moved to the vision station by the Devicenet program. Once there it is checked for correctness. After this it is moved to the eject station where it is ejected if there was a problem. Otherwise it travels to a pickup station.
Most of the control programs in the workcell were completely Linux based, including the CNC machine controller, the DeviceNet master, and database. Communication programs for the robot and vision system were written in Linux, although they required supplemental programming in native languages of the devices.
Conclusion
Many supporters of Linux promote academic use because it is less expensive. While this is true it is a better academic choice because it is more powerful and flexible. These differences become harshly apparent when trying to implement high level systems that go beyond the single user, single computer model. In this paper an example of the use of Linux for a senior level course was presented, thus illustrating the power of the system.