CHAPTER 12 - MAXIMUM TORQUE PATH PLANNING
12.1 Introduction:
The typical limitation of robotic manipulators is joint torque limits. When a robot is to be moved, a torque must be applied to at least one joint. When a motive torque is applied to one or more joints, it tends to elicit a reaction torque in other joints. The result is a very intricate problem of choosing torques that will move the manipulator, while not violating torque limits on the joints.
This problem becomes more complex when the robot must move as fast as possible. The problem of determining joint torques is no longer just finding a solution, but finding the best solution. The optimization problem was discussed in the previous chapter, but this approach takes time (in the order of CPU minutes). If the Optimal Paths determined by these routines could be taught to the neural network, then it would be possible to use the network to approximate optimal paths in real time.
As was done before, a set of optimal paths was determined for the manipulator motion, and these were used to create training and testing sets. These sets were then used to train the neural network, and to test it.
12.2 Maximum Torque Motion:
The motion plans used in this chapter are based on the maximum torque principles that were discussed in the previous chapter. These paths are near optimal, and thus may be used as reasonable examples of optimal paths with maximum torque control. The 10 test cases of the previous chapter will serve as the basis of comparison in this chapter.
12.3 A Neural Network for Maximum Torque Control:
Maximum torque control requires a specific set of inputs. The system state must be fully described, thus position and velocity become controller inputs. The reason for this may be made obvious by observation of the forward and inverse dynamic equations of the manipulator (seen earlier). The equations for dynamics rely heavily upon positions and velocities of joints to determine any robot torque or acceleration.
This neural network should use torque as an output, because acceleration outputs are not necessarily bounded. If the neural network, which has bounded outputs, is expected to produce unbounded outputs, there are some obvious problems. At a singularity, the robot may reach very high accelerations, but the torque limit can be maintained.
Thus, to determine torque, the equations would require position, velocity and goal position. The neural network should use the distance to the goal, with the position and velocity, to determine its own internal representation of acceleration (or equivalent), and subsequently estimate a control torque.
Figure 12.1: Maximum Torque Controller for Robot
Testing this controller is a sophisticated procedure. The Maximum Acceleration and Velocity planners gave outputs of velocity and acceleration. It was easy to derive robot positions, velocities, accelerations, and torques from these values. When torque is used as the network output, as it is here, a more sophisticated method must be used for controller testing (and simulation).
12.4 Simulating the Maximum Torque Neural Network Control:
Testing requires a simulation of the robot dynamics when exposed to joint torques. The torque specified by the neural network will be used as a constant over the system time step. Thus, it is assumed that the position and velocity of the robot is known at the start of the time step. The objective is to find the position and velocity of the manipulator after the time step (with the constant torques applied).
To find motion over a time step, a numerical integration of the equations of motion is required. The dynamic equations discussed earlier are used with the adaptive time step Runge-Kutta algorithm, which is discussed in the appendices. This method is very reliable, and will produce a high quality integration over a motion.
To test the Neural Network as it controls motion, the basic procedure is as follows,
This routine produces highly accurate results in very short times. The simulation runs at better than real time on a Sun Sparcstation, for the particular manipulator case (typical run times for the simulation are about 1 second).
12.5 Results:
The neural network was trained, as before, with a training set, and verified with a testing set. There were a total of 542 training points in the training set, and 532 testing points in the test set. These sets of training and testing points were obtained from the optimal paths, as described earlier, using the Optimal Torque Path Generation Routines.
The network was trained for 30,000 iterations. This gave results as seen in the graphs. All plots have levelled out, thus showing that training was complete, and the network had converged. When observing the difference between the training and testing plots, it becomes obvious that the network does not agree between sets, thus the network had not generalized. This was not acceptable. Thus, the training and test sets were joined, to give a total training set length of 1074 points, and training was continued for another 25,000 iterations (the original test set was still used for testing). The problems remain at the end of this training session, but are reduced. These suggest problems in training, which could be the result of network architecture, training set errors (i.e., non-optimal paths), or too few training points to represent the nature of the optimization solution. Thus, future research should attempt to refine this by the application of the suggestions at the end of the next chapter. (After the training and testing sets were joined, the statistical value of the test set became insignificant.)
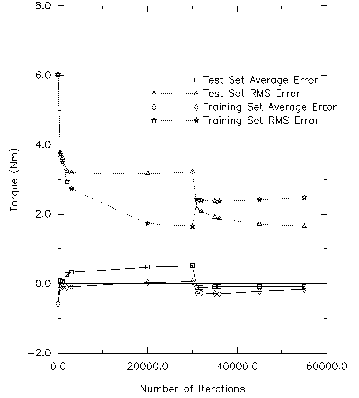
Figure 12.2: Neural Network Convergence for Maximum Torque Planner
The planner was tested with the 10 test cases discussed in earlier chapters. These 10 test cases were directly compared to the path times for the test cases used to test the optimization routines of the last chapter. The assumption is that, these cases should ideally match the path times that the optimization routines produce, since the neural network training data is based on the optimization routines. The test cases may be seen at the end of this chapter.
Figure 12.3: Neural Network Convergence Statistics
The network was tested with the test cases. All the test cases found the goal position, but none did it in the near-optimal time. The table below compares the ideal to the neural network times. The path was determined to be complete, for both the optimization and the neural network, when the joints were within 5 degrees of their final position.
Figure 12.4: Path Times for Test Paths
As can be seen the path times were comparable, but sometimes almost three times more. There are some problem features that distinguish the ability of the neural network to estimate the solution.
The path shapes do vary visibly, and sometimes enormously. The actual differences in path shape may be ignored when evaluating neural network performance. This is because as the path is followed, the small torque estimation differences accumulate, until they become large. This will result in different path shapes, for paths that have similar optimal torque features.
Despite the differences in each of the paths produced by the Neural network, all the paths share a large number of features in common with the optimal version. The torque curves form the best basis of comparison. In all of these the torques do not always have maximum values, but the relative magnitude of the torques is similar. This is encouraging, because it means that the neural network results could be scaled, to produce the desired outputs (as is done in the next chapter).
The neural network also tended to learn the problems that the optimization routines had. Recall that the Optimization routines experienced difficulties with short paths. The short path in test cases 6 and 9 both experienced problems. The problems did seem mainly due to the time step problem, to be mentioned later in this chapter.
The neural network seemed to have problems determining where to switch the torques. This ended up producing some unneeded torque reversals at path midpoints. This problem occurred for cases 1, 3, 5, 8 and 10. These paths also have the feature of having long ranges of motion.
Thus, there are two dominant problems which appear to occur. One is with paths that are short, and the other occurs with paths that are long.
Figure 12.5: Maximum Torque Control With a Neural Network, Case 1
Figure 12.6: Maximum Torque Control With a Neural Network, Case 2
Figure 12.7: Maximum Torque Control With a Neural Network, Case 3
Figure 12.8: Maximum Torque Control With a Neural Network, Case 4
Figure 12.9: Maximum Torque Control With a Neural Network, Case 5
Figure 12.10: Maximum Torque Control With a Neural Network, Case 6
Figure 12.11: Maximum Torque Control With a Neural Network, Case 7
Figure 12.12: Maximum Torque Control With a Neural Network, Case 8
Figure 12.13: Maximum Torque Control With a Neural Network, Case 9
Figure 12.14: Maximum Torque Control With a Neural Network, Case 10
To aid the reader in analysis of the results, composite graphs of positions are given below. These graphs combine the results of the previous chapter, and the results shown here.
Figure 12.15: Comparison of Neural Network to “Ideal” Solution
Figure 12.15(continued): Comparison of Neural Network to “Ideal” Solution
Figure 12.15(continued): Comparison of Neural Network to “Ideal” Solution
12.6 Conclusions:
The problems that were uncovered in the results suggest that some further investigation is required. It is known that the training region size will effect the quality of performance by neural networks [Lee et. al., 1990][Jack et. al., unpublished]. Here the neural network was trained to the borders of the training region. When the neural network is expected to operate near these boundaries, there is an obvious decay in performance (see cases 1, 3, 5, 6, and 10). The solution to this problem is simple, the areas of the training region should be expanded. (i.e., expand the training region from -180 to 180 possibly to -270 to 270)
Another problem arose when the path was too short. This problem is, as the neural network nears the goal, the network no longer produces optimal torques (at the bang-bang levels).
The sample joint position and torque graphs below illustrate that if the time step of the system is decreased enough, the aliasing problem will disappear. The graphs show a major problem with a time step of 0.20 seconds. The convergence to the goal position is slow, and the torques flutter. A time step of 0.10 shows the system is more stable, but still tends to oscillate. Finally, at 0.05 seconds, the results converge very quickly, and with no flutter. The test cases were all examined with the system time step set at 0.10 seconds. This may be explained with the Nyquist Criterion. As the sampling frequency of the controller approaches the natural frequency of the system, the control becomes unstable.
Figure 12.16: Test Case With Time Step of 0.05 seconds
Figure 12.17: Test Case With Time Step of 0.10 seconds
Figure 12.18: Test Case With Time Step of 0.20 seconds