COORDINATE SYSTEMS
35.4.1 Complex Numbers
• In this section, as in all others, ‘j’ will be the preferred notation for the complex number, this is to help minimize confusion with the ‘i’ used for current in electrical engineering.
• The basic algebraic properties of these numbers are,
• We can also show complex numbers graphically. These representations lead to alternative representations. If it in not obvious above, please consider the notation above uses a cartesian notation, but a polar notation can also be very useful when doing large calculations.
• We can also do calculations using polar notation (this is well suited to multiplication and division, whereas cartesian notation is easier for addition and subtraction),
• Note that DeMoivre’s theorem can be used to find exponents (including roots) of complex numbers
• Euler’s formula: 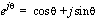
• From the above, the following useful identities arise:
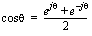

35.4.2 Cylindrical Coordinates
• Basically, these coordinates appear as if the cartesian box has been replaced with a cylinder,
35.4.3 Spherical Coordinates
• This system replaces the cartesian box with a sphere,
35.4.4 Practice Problems
1. Simplify the following expressions.
2. For the shape defined below,