SPATIAL RELATIONSHIPS
35.3.1 Trigonometry
• The basic trigonometry functions are,
• Graphs of these functions are given below,
• NOTE: Keep in mind when finding these trig values, that any value that does not lie in the right hand quadrants of cartesian space, may need additions of ±90° or ±180°.
• Now a group of trigonometric relationships will be given. These are often best used when attempting to manipulate equations.
• Numerical values for these functions are given below.
• These can also be related to complex exponents,
35.3.2 Hyperbolic Functions
• The basic definitions are given below,
• some of the basic relationships are,
• Some of the more advanced relationships are,
• Some of the relationships between the hyperbolic, and normal trigonometry functions are,
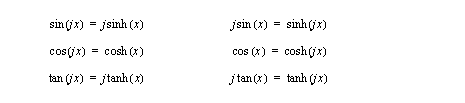
35.3.2.1 - Practice Problems
1. Find all of the missing side lengths and corner angles on the two triangles below.
2. Simplify the following expressions.
3. Solve the following partial fraction
35.3.3 Geometry
• A set of the basic 2D and 3D geometric primitives are given, and the notation used is described below,
• A general class of geometries are conics. This for is shown below, and can be used to represent many of the simple shapes represented by a polynomial.
35.3.4 Planes, Lines, etc.
• The most fundamental mathematical geometry is a line. The basic relationships are given below,
• If we assume a line is between two points in space, and that at one end we have a local reference frame, there are some basic relationships that can be derived.
• The relationships for a plane are,
35.3.5 Practice Problems
1. What is the circumferenece of a circle? What is the area? What is the ratio of the area to the circumference?
2. What is the equation of a line that passes through the points below?
3. Find a line that is perpendicular to the line through the points (2, 1) and (1, 2). The perpendicular line passes through (3, 5).
4. Manipulate the following equations to solve for ‘x’.
5. Simplify the following expressions.
6. A line that passes through the point (1, 2) and has a slope of 2. Find the equation for the line, and for a line perpendicular to it.