FUNCTIONS

 

Figure 35.9 Distribution functions

• The quadratic equation appears in almost every engineering discipline, therefore is of great importance.

 

Figure 35.10 Quadratic equation

• Cubic equations also appear on a regular basic, and as a result should also be considered.

 

Figure 35.11 Cubic equations

• On a few occasions a quartic equation will also have to be solved. This can be done by first reducing the equation to a quadratic,

 

Figure 35.12 Quartic equations

• The next is a flowchart for partial fraction expansions.

 

Figure 35.13 The methodolgy for solving partial fractions

• The partial fraction expansion for,

 

Figure 35.14 A partial fraction example

• Consider the example below where the order of the numerator is larger than the denominator.

 

Figure 35.15 Solving partial fractions when the numerator order is greater than the denominator

• When the order of the denominator terms is greater than 1 it requires an expanded partial fraction form, as shown below.

 

Figure 35.16 Partial fractions with repeated roots

• We can solve the previous problem using the algebra technique.

 

Figure 35.17 An algebra solution to partial fractions

• The notation 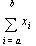is equivalent to 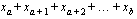assuming 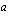and 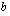are integers and 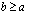. The index variable 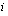is a placeholder whose name does not matter.

• Operations on summations:

 

 

 

 

 

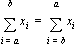
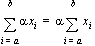
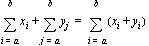
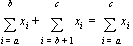
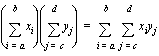
• Some common summations:

 

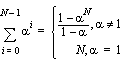for both real and complex .

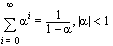for both real and complex . For 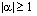, the summation does not converge.

1. Convert the following polynomials to multiplied terms as shown in the example.

2. Solve the following equation to find ‘x’.

 

3. Reduce the following expression to partial fraction form.