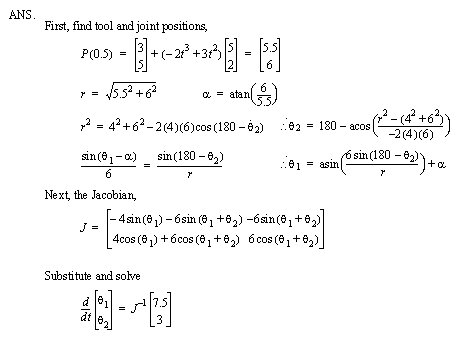
• Basically mechanisms that are 3D (not planar).
• When we deal with geometries in two dimensions we have three position variables (dof) for each rigid body (two for position, one for orientation).
• When a problem is expanded to three dimensions we then have six position variables (dof) for a rigid body (three for position, and three for orientation).
• These added degrees of freedom expand the complexity of the problem solutions. There are a few potential approaches,
- look for regularities that simplify the problem (scalar)
- vector based approaches (positions)
- matrix based approaches (positions and orientations)
• Consider the example of the spherical joint - all of the axes of rotation coincide.

• The scalar and vector approaches are easily extended to 3D problems. One significant difference is that the polar notations are no longer available for use.
• We can determine the number of degrees of freedom using a simple relationship that is an extension of the Kutzbach criteria,

• Consider the number of degrees of freedom in the linkage below,
• This method still uses geometry to determine the position of the robot, but it is put into an ordered method using matrices.
• Consider the planar robot below,
• The basic approach to this method is,
1. On the base, each joint, and the tool of the robot, attach a reference frame (most often x-y-z). Note that the last point is labels ‘T’ for tool. This will be a convention that I will generally follow.
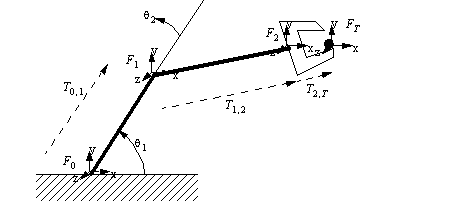
2. Determine a transformation matrix to map between each frame. It is important to do this by assuming the joints are in their 0 joint positions. Put the joint positions in as variables.
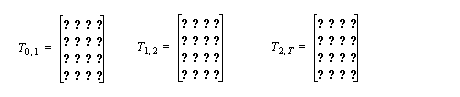
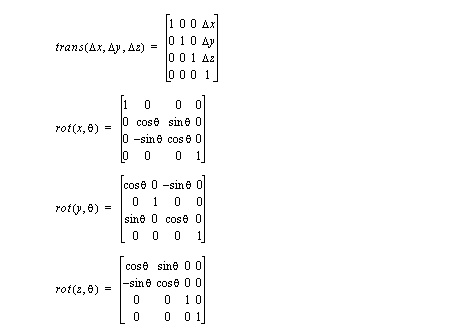
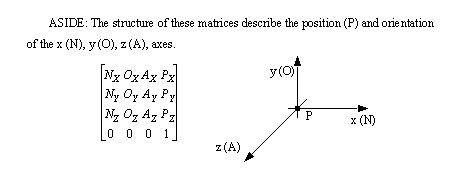

3. Multiply the frames to get a complete transformation matrix.
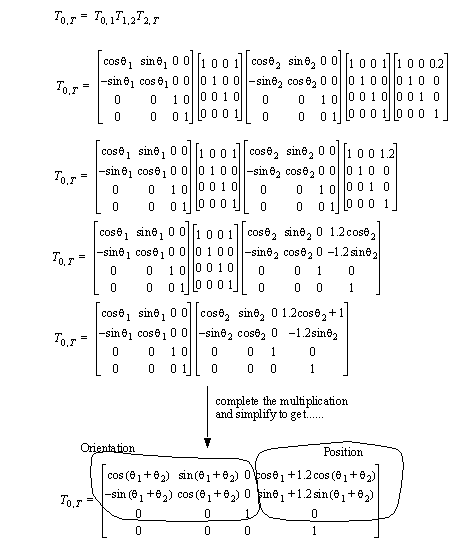
• The position and orientation can be read directly from the homogenous transformation matrix as indicated above.
• To reverse the transform, we only need to invert the transform matrix - this is a direct result of the loop equation.

• Designed as more specialized transforms for robots (based on homogenous transforms)
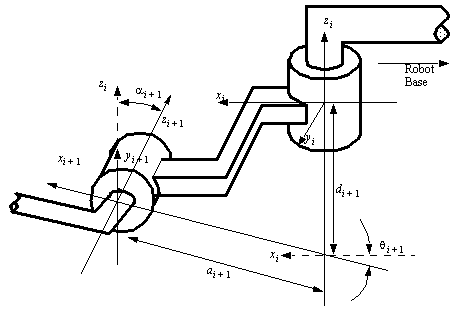
• Zi-1 axis along motion of ith joint
• Xi axis normal to Zi-1 axis, and points away from it.
1. rotate about Zi-1 by thetai (joint angle)
2. translate along Zi-1 by di (link offset)
3. translate along Xi by ai (link length)
4. rotate about Xi by alphai (link twist)
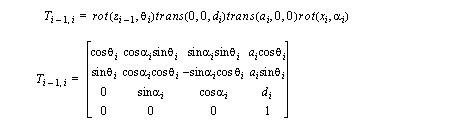
• We can see how the D-H representation is applied using the two link manipulator from before
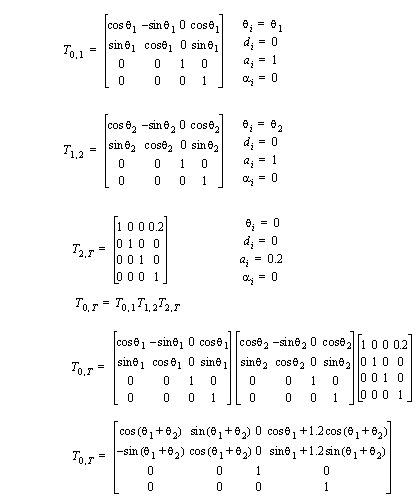
• The Euler angles are a very common way to represent orientation in 3-space.
• The main problem in representing orientation is that the angles of rotation must be applied one at a time, and by changing the sequence we will change the final orientation. In other words the three angles will not give a unique solution unless applied in the same sequence every time.
• By fixing a set of angles by convention we can then use the three angles by themselves to define an orientation.
• The convention described here is the Euler angles.
• The sequence of orientation is,
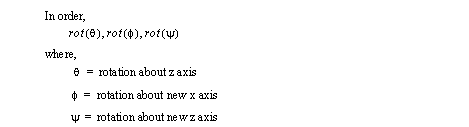
• Therefore to reorient a point in space we can apply the following matrix, to the position vectors, or axes vectors, (there will be more on these matrices shortly)

• We can find these angles given a set of axis before and after.
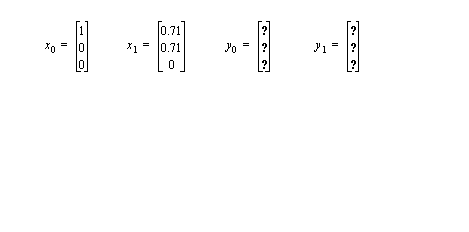
• Basically we can find the joint angles for the robot based on the position of the end effector.
• This is not a simple problem, and there are few reliable methods. This is partly caused by the non-unique nature of the problem. At best there are typically multiple, if not infinite numbers of equivalent solutions. The 2 dof robot seen before has two possible solutions.
• We can do simple inverse kinematics with trigonometry.
• If we have more complicated problems, we may try to solve the problem by examining the transform matrix,

• A matrix of partial derivatives that relate the velocity of the joints, to the velocity of the tool.
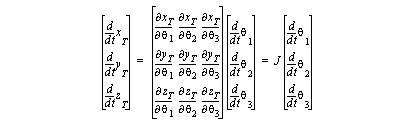
• The inverse Jacobian is used for motion control
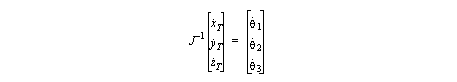
• Find the Jacobian and inverse Jacobian for the 2 dof robot.

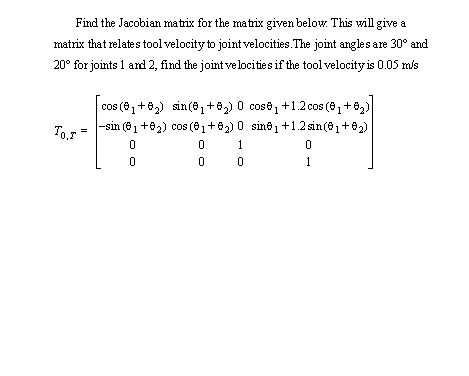
• The basic principles of planar dynamics are expanded up for 3D spatial problems. The added dimension adds some complexity that should be addressed.
• Moments of Inertia are normally found for a single axis of rotation. When the object is rotating about another axis, we must recalculate the moments of inertia.
• If we take the moments of inertia for the original axes, and project these values onto new vectors, we can get new values,
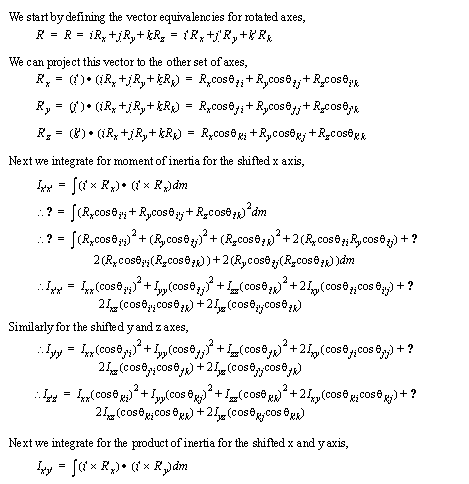
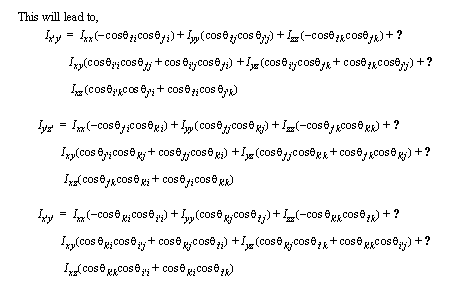
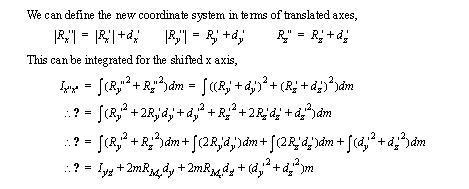
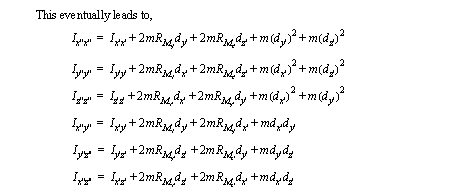
• We can use Euler’s equations of motion to determine moments produced by angular velocities and accelerations.
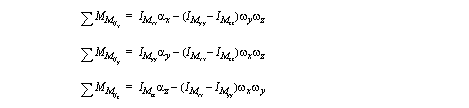
• These can be used to examine rotating three dimensional masses. Consider the following,
• Momentum is a convenient alternative to energy in analysis of systems.

• If no external forces are applied, momentum remains constant (is conserved). In this case L is a constant.
• Angular momentum is for rotating objects. The rotation about some center tends to make these equations a bit more complicated than linear momentum.
• We can start to find this as a velocity times a distance of rotation, and this will lead to the eventual relationships,
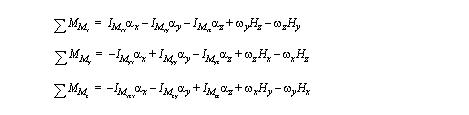
• These equations show the angular momentum H, along with other familiar terms.
• There are a variety of common methods,
- Euler-Lagrange - energy based
• This method uses a Lagrangian energy operator to calculate torques
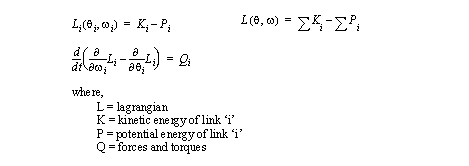
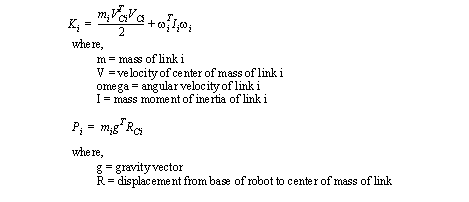
• If we have used matrices to formulate the problem, we use the Jacobian to find velocities.

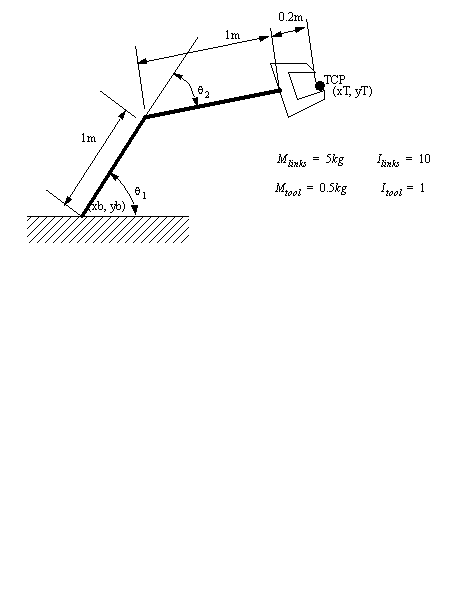
• We can sum forces and moments, and then solve the equations in a given sequence.

• These equations can be written in vector form,

• To do these calculations start at the base, and calculate the kinematics up to the end of the manipulator (joint positions, velocities and accelerations). Then work back from the end and find forces and moments.
Erdman, A.G. and Sandor, G.N., Mechanism Design Analysis and Synthesis, Vol. 1, 3rd Edition, Prentice Hall, 1997.
Shigley, J.E., Uicker, J.J., “Theory of Machines and Mechanisms, Second Edition, McGraw-Hill, 1995.
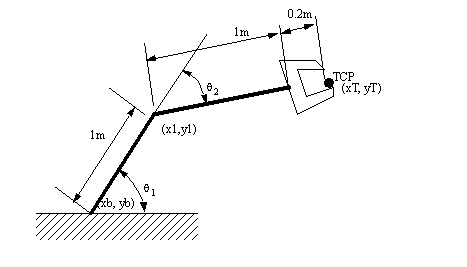
1. For the Stanford arm below,
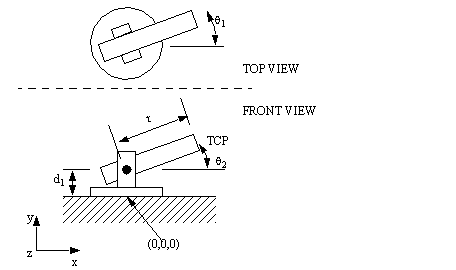
a) list the D-H parameters (Hint: extra “dummy” joints may be required)
b) Find the forward kinematics using homogenous matrices.
c) Find the Jacobian matrix for the arm.
d) If the arm is at θ1 = 45 degrees, θ2 = 45 degrees, r = 0.5m, find the speed of the TCP if the joint velocities are θ’1 = 1 degree/sec, θ’2 = 10 degrees/sec, and r’ = 0.01 m/sec.
3. Robotics and Automated Manipulators (RAM) has consulted you about a new robotic manipulator. This work will include kinematic analysis, gears, and the tool. The robot is pictured below. The robot is shown on the next page in the undeformed position. The tool is a gripper (finger) type mechanism.

The robot is drawn below in the undeformed position. The three positioning joints are shown, and a frame at the base and tool are also shown.

The tool is a basic gripper mechanism, and is shown as a planar mechanism below. As the cylinder moves to the left the fingers close.
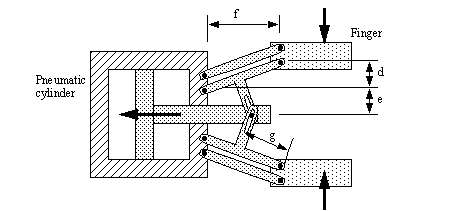
a) The first thing you do is determine what sequence of rotations and translations are needed to find the tool position relative to the base position.
b) As normal, you decide to relate a cartesian (x-y) velocity of the gripper to joint velocities. Set up the calculation steps needed to do this based on the results in question #1.
c) To drive the revolute joints RAM has already selected two similar motors that have a maximum velocity. You decide to use the equations in question #2, with maximum specified tool velocities to find maximum joint velocities. Assume that helical gears are to be used to drive the revolute joints, specify the basic dimensions (such as base circle dia.). List the steps to develop the geometry of the gears, including equations.
d) The gripper fingers may close quickly, and as a result a dynamic analysis is deemed necessary. List the steps required to do an analysis (including equations) to find the dynamic forces on the fingers.
e) The idea of using a cam as an alternate mechanism is being considered. Develop a design that is equivalent to the previous design. Sketch the mechanism and a detailed displacement graph of the cam.
f) The sliding joint ‘r’ has not been designed yet. RAM wants to drive the linear motion, without using a cylinder. Suggest a reasonable design, and sketch.
4. For an articulated robot, find the forward, and inverse kinematics using geometry, homogenous matrices, and Denavit-Hartenberg transformations.
5. Assign Denavit-Hartenberg link parameters to an articulated robot.
6. For the Stanford arm below,
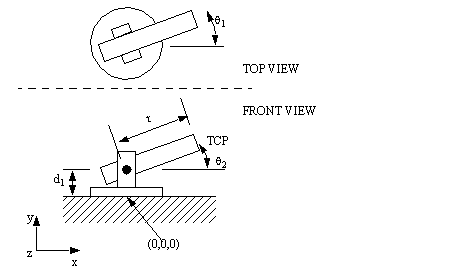
a) list the D-H parameters (Hint: extra “dummy” joints may be required)
b) Find the forward kinematics using homogenous matrices.
c) Find the Jacobian matrix for the arm.
d) If the arm is at θ1 = 45 degrees, θ2 = 45 degrees, r = 0.5m, find the speed of the TCP if the joint velocities are θ’1 = 1 degree/sec, θ’2 = 10 degrees/sec, and r’ = 0.01 m/sec.
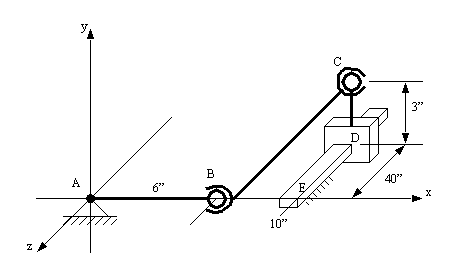
7. Consider the forward kinematic transformation of the two link manipulator below. Given the position of the joints, and the lengths of the links, determine the location of the tool centre point using a) basic geometry, b) homogenous transforms, and c) Denavit-Hartenberg transformations.
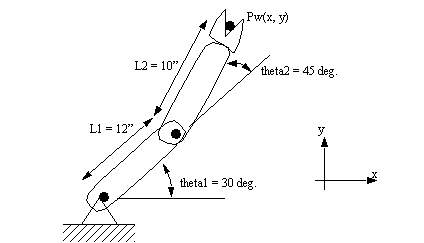
a) For the robot described in question 1 determine the inverse kinematics for the robot. (i.e., given the position of the tool, determine the joint angles of the robot.) Keep in mind that in this case the solution will have two different cases. Determine two different sets of joint angles required to position the TCP at x=5”, y=6”.
b) For the inverse kinematics of question #2, what conditions would indicate the robot position is unreachable? Are there any other cases that are indeterminate?
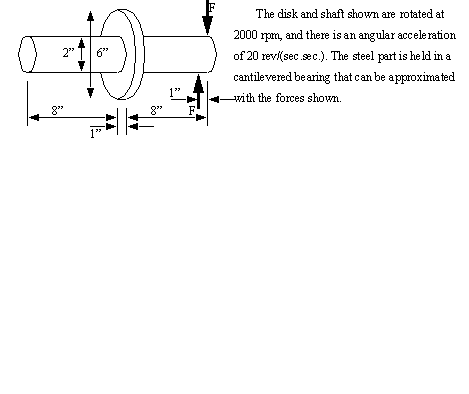
8 Find the dynamic forces in the system below,
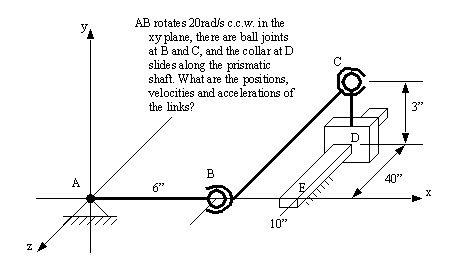
9. Examine the robot figure below and,
a) assign frames to the appropriate joints.
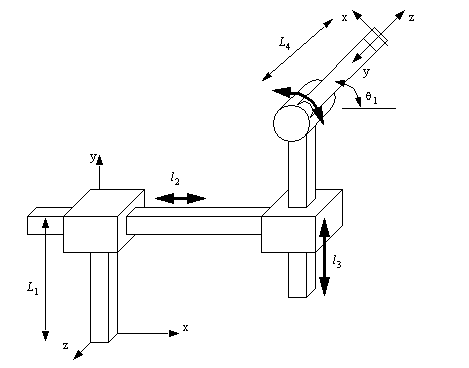

b) list the transformations for the forward kinematics.

c) expand the transformations to matrices (do not multiply).

10. Given the transformation matrix below for a polar robot,
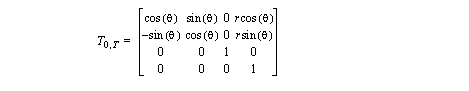
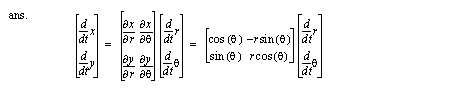
b) Given the joint positions, find the forward and inverse Jacobian matrices.


c) If we are at the position below, and want to move the tool at the given speed, what joint velocities are required?
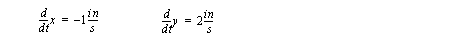
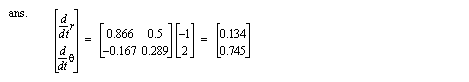
11. Examine the robot figure below and,
a) assign frames to the appropriate joints.

b) list the transformations for the forward kinematics.
c) expand the transformations to matrices (do not multiply).
12. Given the transformation matrix below for a polar robot,
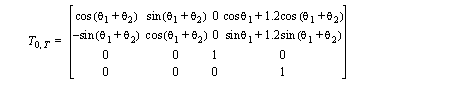
b) Given the joint positions, find the forward and inverse Jacobian matrices.

c) If we are at the position below, and want to move the tool at the given speed, what joint velocities are required?

13. Find the forward kinematics for the robots below using homogeneous and Denavit-Hartenberg matrices.

14. Use the equations below to find the inverse Jacobian. Use the inverse Jacobian to find the joint velocities required at t=0.5s.