3.8.1 Partial Fractions
• The next is a flowchart for partial fraction expansions.
• The partial fraction expansion for,
• Consider the example below where the order of the numerator is larger than the denominator.
• When the order of the denominator terms is greater than 1 it requires an expanded partial fraction form, as shown below.
• We can solve the previous problem using the algebra technique.
3.8.2 Summation and Series
• The notation  is equivalent to
is equivalent to 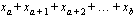 assuming
assuming 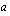 and
and 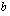 are integers and
are integers and 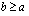 . The index variable
. The index variable  is an index often replaced with j, k, m, and n.
is an index often replaced with j, k, m, and n.
• Operations on summations:

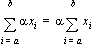
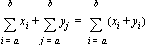
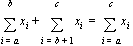
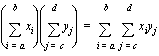
• Some common summations:
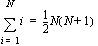
 for both real and complex
for both real and complex 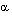 .
.
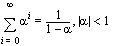 for both real and complex
for both real and complex 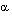 . For
. For 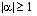 , the summation does not converge.
, the summation does not converge.
• In Scilab