5.1 Introduction5.1.1 InertiaWhen unbalanced torques are applied to a mass it will begin to accelerate, in rotation. The sum of applied torques is equal to the inertia forces shown in Figure 1.23 Summing moments and angular inertia. 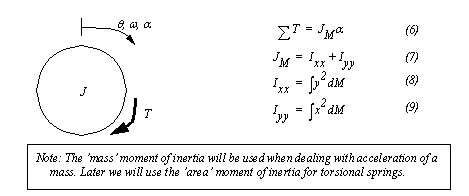
The mass moment of inertia determines the resistance to acceleration. This can be calculated using integration, or found in tables. When dealing with rotational acceleration it is important to use the mass moment of inertia, not the area moment of inertia. The center of rotation for free body rotation will be the centroid. Moment of inertia values are typically calculated about the centroid. If the object is constrained to rotate about some point, other than the centroid, the moment of inertia value must be recalculated. The parallel axis theorem provides the method to shift a moment of inertia from a centroid to an arbitrary center of rotation, as shown in Figure 1.24 Parallel axis theorem for shifting a mass moment of inertia. 


An example of calculating a mass moment of inertia is shown in Figure 1.26 Mass moment of inertia example. In this problem the density of the material is calculated for use in the integrals. The integrals are then developed using slices for the integration element dM. The integrals for the moments about the x and y axes, are then added to give the polar moment of inertia. This is then shifted from the centroid to the new axis using the parallel axis theorem. 
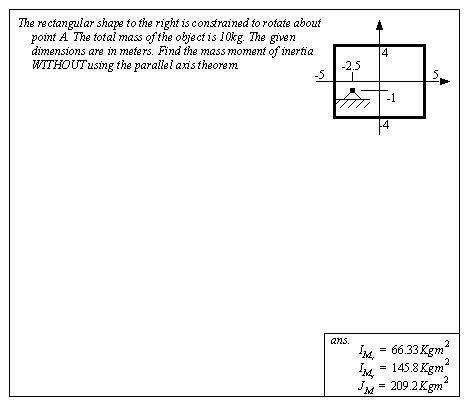

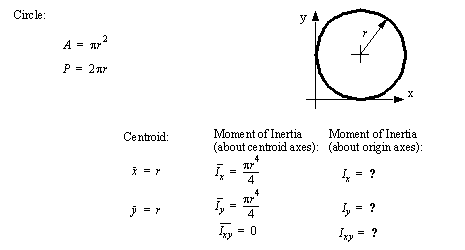
• A set of the basic 2D and 3D geometric primitives are given, and the notation used is described below, 


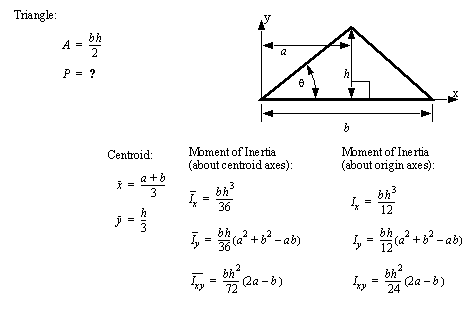
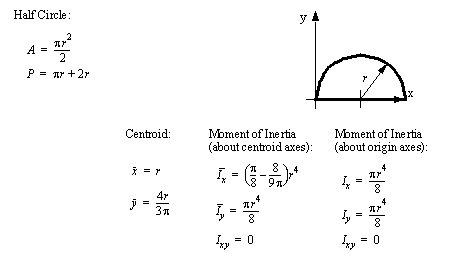

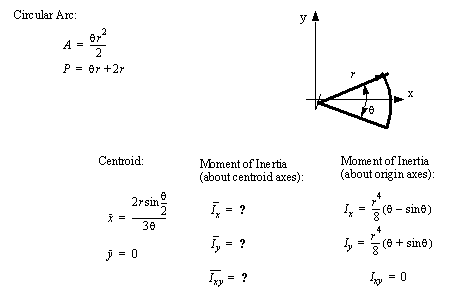
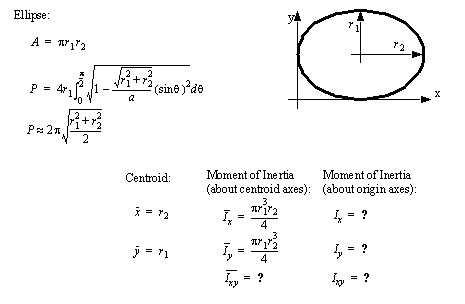
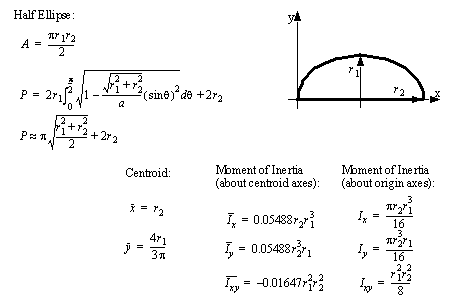
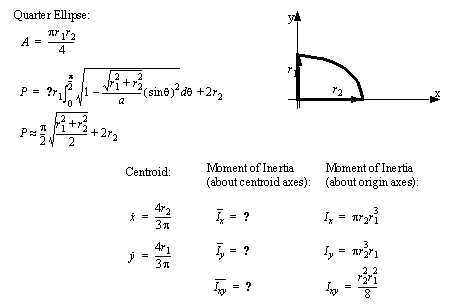
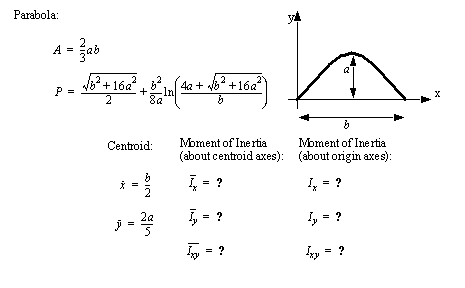
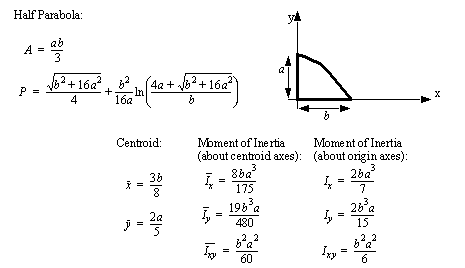
• A general class of geometries are conics. This for is shown below, and can be used to represent many of the simple shapes represented by a polynomial. 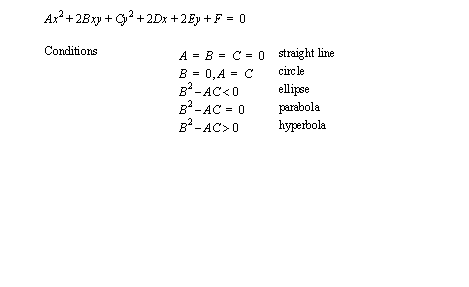

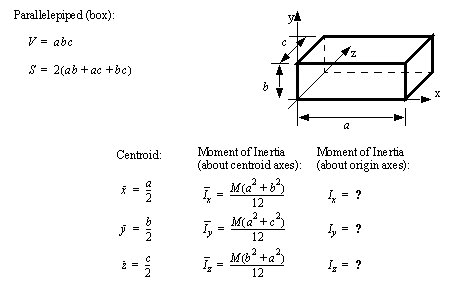
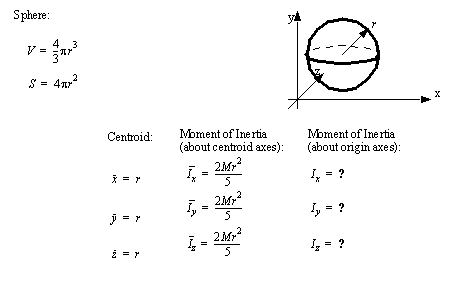
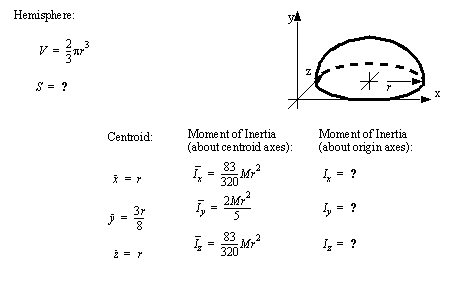

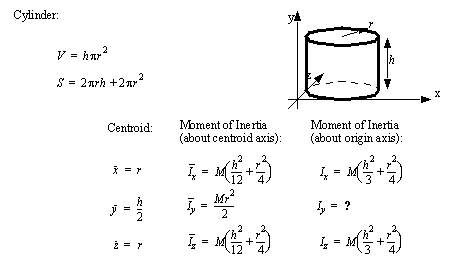
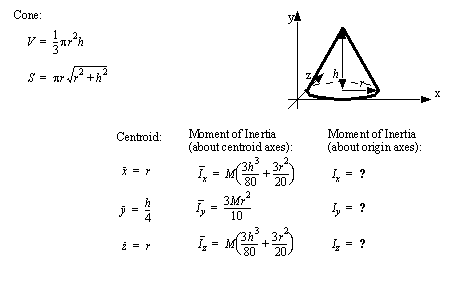
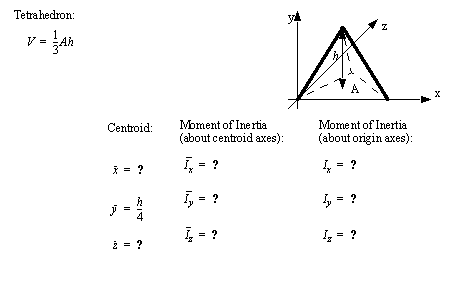
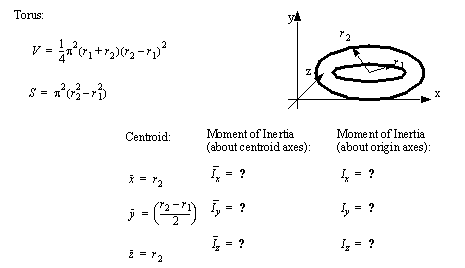
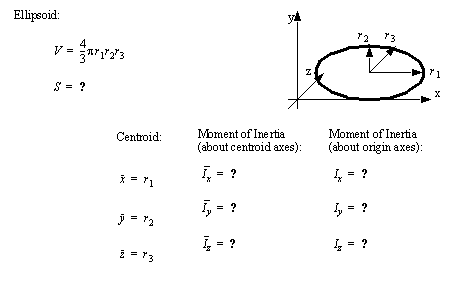
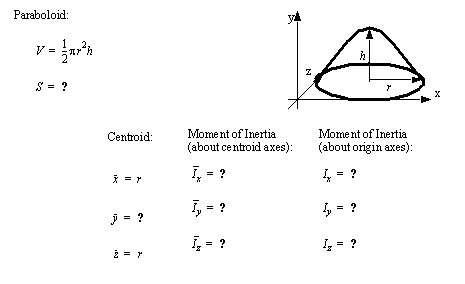
|