19. SEQUENTIAL FUNCTION CHARTS• Describing process control SFCs • Conversion of SFCs to ladder logic • Learn to recognize parallel control problems. • Be able to develop SFCs for a process. • Be able to convert SFCs to ladder logic. All of the previous methods are well suited to processes that have a single state active at any one time. This is adequate for simpler machines and processes, but more complex machines are designed perform simultaneous operations. This requires a controller that is capable of concurrent processing - this means more than one state will be active at any one time. This could be achieved with multiple state diagrams, or with more mature techniques such as Sequential Function Charts. Sequential Function Charts (SFCs) are a graphical technique for writing concurrent control programs. (Note: They are also known as Grafcet or IEC 848.) SFCs are a subset of the more complex Petri net techniques that are discussed in another chapter. The basic elements of an SFC diagram are shown in Figure 19.1 Basic Elements in SFCs and Figure 19.1 Basic Elements in SFCs. 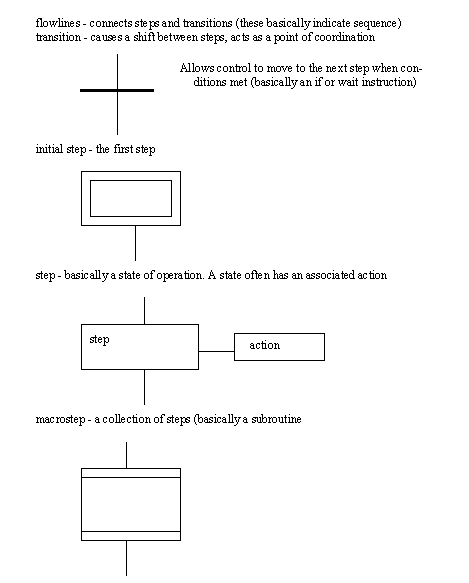
Figure 19.1 Basic Elements in SFCs 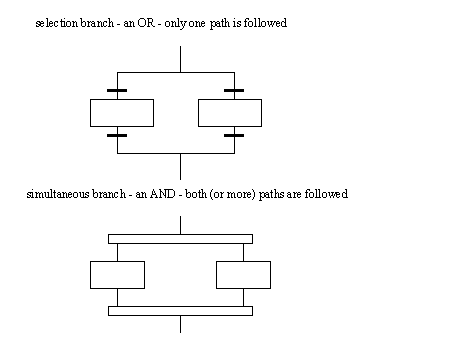
Figure 19.1 Basic Elements in SFCs The example in Figure 19.1 SFC for Control of Two Doors with Security Codes shows a SFC for control of a two door security system. One door requires a two digit entry code, the second door requires a three digit entry code. The execution of the system starts at the top of the diagram at the Start block when the power is turned on. There is an action associated with the Start block that locks the doors. (Note: in practice the SFC uses ladder logic for inputs and outputs, but this is not shown on the diagram.) After the start block the diagram immediately splits the execution into two processes and both steps 1 and 6 are active. Steps are quite similar to states in state diagrams. The transitions are similar to transitions in state diagrams, but they are drawn with thick lines that cross the normal transition path. When the right logical conditions are satisfied the transition will stop one step and start the next. While step 1 is active there are two possible transitions that could occur. If the first combination digit is correct then step 1 will become inactive and step 2 will become active. If the digit is incorrect then the transition will then go on to wait for the later transition for the 5 second delay, and after that step 5 will be active. Step 1 does not have an action associated, so nothing should be done while waiting for either of the transitions. The logic for both of the doors will repeat once the cycle of combination-unlock-delay-lock has completed. 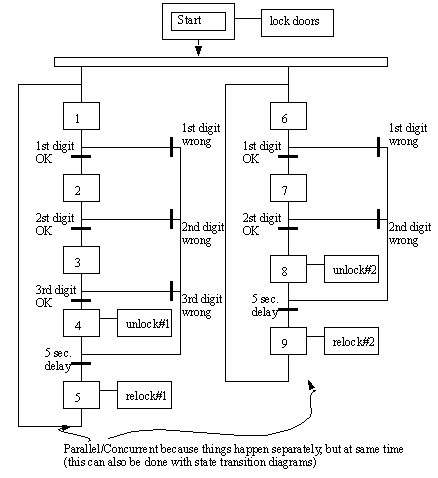
Figure 19.1 SFC for Control of Two Doors with Security Codes A simple SFC for controlling a stamping press is shown in Figure 19.1 SFC for Controlling a Stamping Press. (Note: this controller only has a single thread of execution, so it could also be implemented with state diagrams, flowcharts, or other methods.) In the diagram the press starts in an idle state. when an automatic button is pushed the press will turn on the press power and lights. When a part is detected the press ram will advance down to the bottom limit switch. The press will then retract the ram until the top limit switch is contacted, and the ram will be stopped. A stop button can stop the press only when it is advancing. (Note: normal designs require that stops work all the time.) When the press is stopped a reset button must be pushed before the automatic button can be pushed again. After step 6 the press will wait until the part is not present before waiting for the next part. Without this logic the press would cycle continuously. 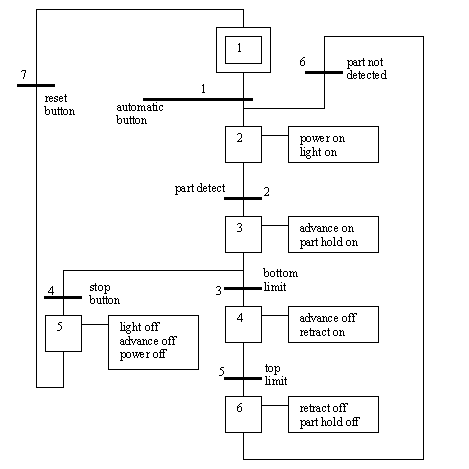
Figure 19.1 SFC for Controlling a Stamping Press The SFC can be converted directly to ladder logic with methods very similar to those used for state diagrams as shown in Figure 19.1 SFC Implemented in Ladder Logic to Figure 19.1 SFC Implemented in Ladder Logic. The method shown is patterned after the block logic method. One significant difference is that the transitions must now be considered separately. The ladder logic begins with a section to initialize the states and transitions to a single value. The next section of the ladder logic considers the transitions and then checks for transition conditions. If satisfied the following step or transition can be turned on, and the transition turned off. This is followed by ladder logic to turn on outputs as requires by the steps. This section of ladder logic corresponds to the actions for each step. After that the steps are considered, and the logic moves to the following transitions or steps. The sequence examine transitions, do actions then do steps is very important. If other sequences are used outputs may not be actuated, or steps missed entirely. 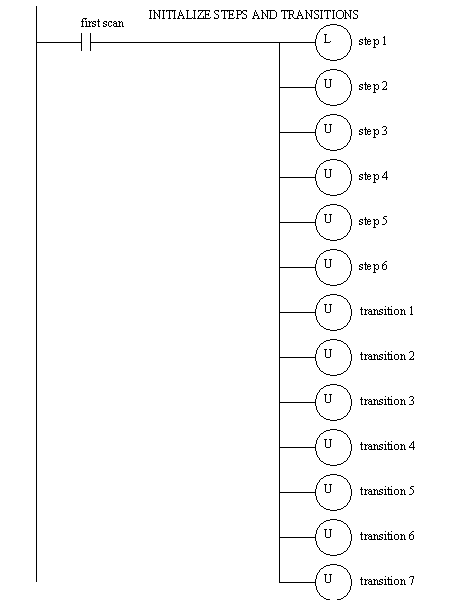
Figure 19.1 SFC Implemented in Ladder Logic 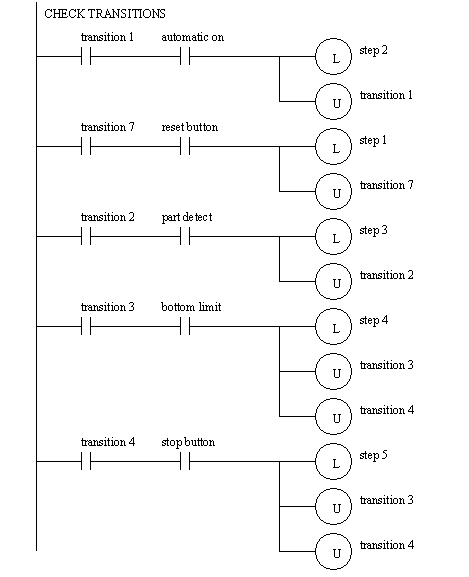
Figure 19.1 SFC Implemented in Ladder Logic 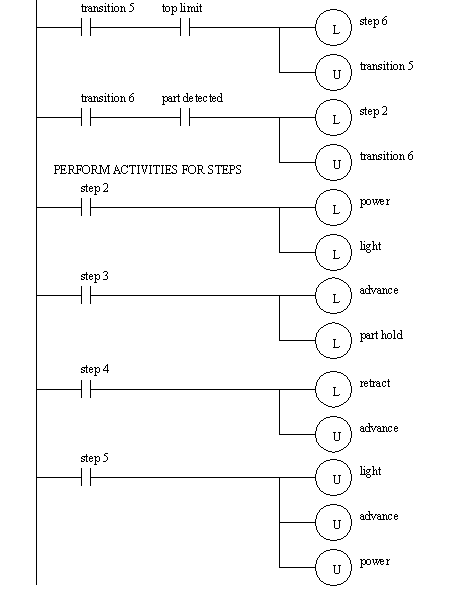
Figure 19.1 SFC Implemented in Ladder Logic 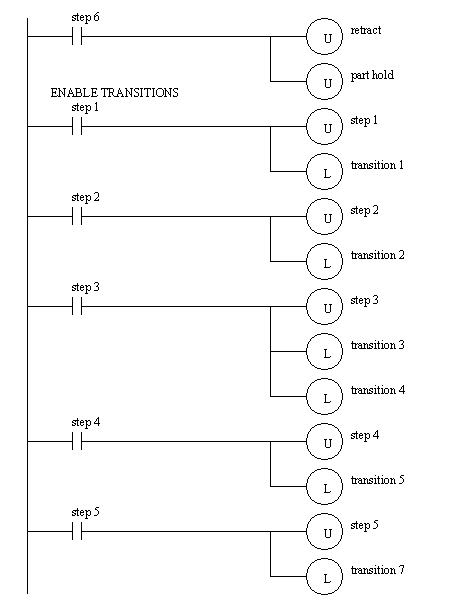
Figure 19.1 SFC Implemented in Ladder Logic 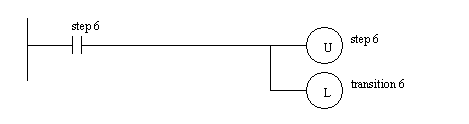
Figure 19.1 SFC Implemented in Ladder Logic Many PLCs also allow SFCs to entered be as graphic diagrams. Small segments of ladder logic must then be entered for each transition and action. Each segment of ladder logic is kept in a separate program. If we consider the previous example the SFC diagram would be numbered as shown in Figure 19.1 SFC Renumbered. The numbers are sequential and are for both transitions and steps. 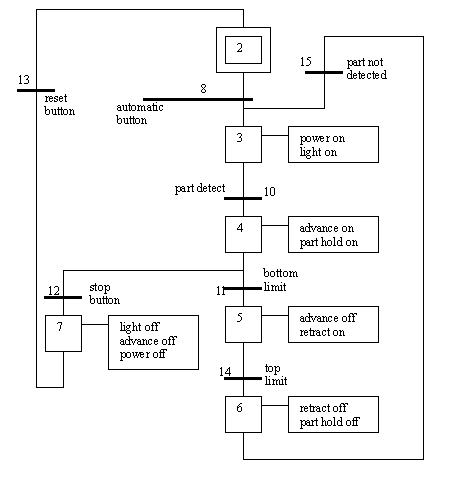
Some of the ladder logic for the SFC is shown in Figure 19.1 Sample Ladder Logic for a Graphical SFC Program. Each program corresponds to the number on the diagram. The ladder logic includes a new instruction, EOT, that will tell the PLC when a transition has completed. When the rung of ladder logic with the EOT output becomes true the SFC will move to the next step or transition. when developing graphical SFCs the ladder logic becomes very simple, and the PLC deals with turning states on and off properly. 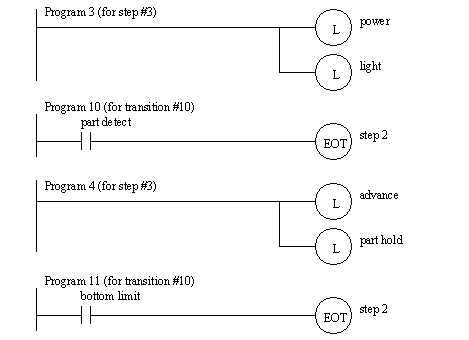
Figure 19.1 Sample Ladder Logic for a Graphical SFC Program SFCs can also be implemented using ladder logic that is not based on latches, or built in SFC capabilities. The previous SFC example is implemented below. The first segment of ladder logic in Figure 19.1 Ladder logic for transitions is for the transitions. The logic for the steps is shown in Figure 19.1 Step logic. 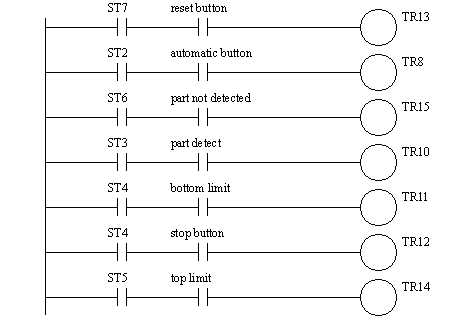
Figure 19.1 Ladder logic for transitions 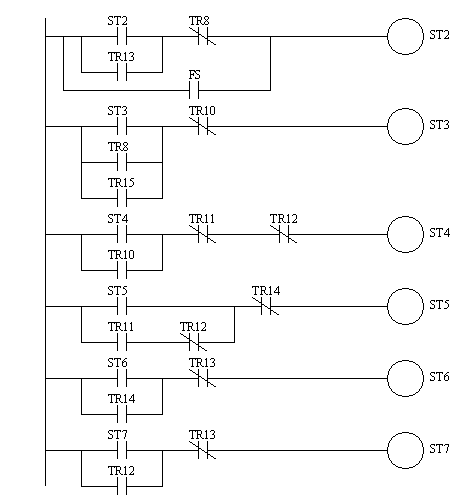

|